VI. Составление и решение выражений.
Выполняя задание 3 (с. 36 учебника, часть 1), дети под руководством учителя составляют выражения и сравнивают их.
8 + 9 < 20 – 1 16 – 8 > 16 – 10
17 < 19 8 > 6
Далее с комментированием выполняется задание 6 (с. 37 учебника, часть 1).
VII. Итог урока.
– Какие открытия сделали на уроке?
– Что такое «периметр»?
– Что бы вам хотелось выполнить ещё?
– Как вы сегодня работали?
У р о к 28. СВОЙСТВА СЛОЖЕНИЯ
Цели:познакомить учащихся ещё с одним свойством сложения, основанным на группировке слагаемых; показать значение данного приёма при вычислениях; формировать умение находить периметр многоугольников; развивать умение определять время по часам; продолжать работу над задачами; развивать навыки счёта.
Ход урока
I. Организационный момент.
II. Каллиграфическая минутка.
28 28 28 28 28
30 30 30 30 30
III. Устный счёт.
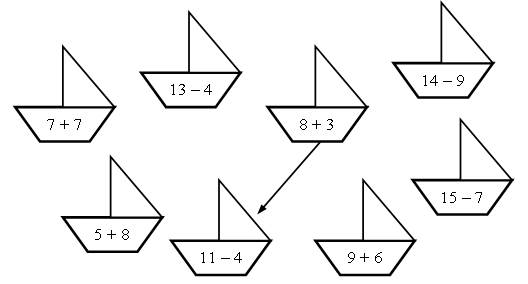
1. Круговые примеры.
2. Какое число пропущено?
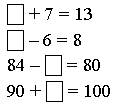
3. Который час?
Работа проводится по заданию 6 (с. 39 учебника, часть 1), его лучше вынести на доску.
– Какие из этих часов показывают правильное время, если сейчас без 15 минут 8 часов? (Правильное время показывают вторые часы.)
– На сколько минут спешат или отстают другие часы? (Первые часы спешат на 5 минут, третьи часы отстают на 20 минут.)
IV. Работа над новым материалом.
Учитель предлагает учащимся рассмотреть сумму чисел, записанную на доске:
5 + 3 + 2 = 10
– Как по-разному можно найти значение данной суммы?
С п о с о б I. Сначала к первому слагаемому 5 прибавим второе слагаемое 3.
(5 + 3) – получим 8.
Затем к числу 8 прибавим третье слагаемое 2.
(5 + 3) + 2 – получим 10.
С п о с о б II. Сначала ко второму слагаемому 3 прибавим третье слагаемое 2.
(3 + 2) – получим 5.
Затем полученное число 5 прибавим к первому слагаемому 5.
5 + (3 + 2) – получим 10.
– Какой способ показался вам более удобным?
Далее отрабатывается прием группировки слагаемых при решении следующих выражений:
1 + 9 + 5
2 + 7 + 3
6 + 1 + 9
Ученики выбирают наиболее удобный способ решения выражений.
Н а п р и м е р:
(1 + 9) + 5 = 10 + 5 = 15
2 + (7 + 3) = 2 + 10 = 12
6 + (1 + 9) = 6 + 10 = 16
После этой работы учитель просит детей сформулировать вывод и сравнить его с правилом, данным в учебнике на с. 38 (часть 1).
Затем учитель предлагает учащимся сравнить суммы, записанные на доске:
4 + (1 + 3)
(4 + 1) + 3
(4 + 3) + 1
1 + (4 + 3)
– Что хотите сказать?
– Как вы думаете, значения этих сумм равны?
– Почему так считаете?
– Какой закон сложения применяли в 3-й и 4-й суммах? (Переместительный.)
– Подумайте, правильно ли будет сказать: если нужно сложить несколько чисел, то их можно складывать в любом порядке, значение суммы при этом не изменится. (Да.)
Далее с подробным устным объяснением выполняется задание 3 (с. 39 учебника, часть 1), в котором дети сравнивают выражения, объясняют, как каждое следующее выражение получено из предыдущего, выбирают наиболее удобный способ решения того или иного выражения.

V. Работа над задачами.
Учащиеся читают текст задачи 4 (с. 39 учебника, часть 1), находят условие и вопрос, называют данные и искомое числа, затем составляют схему-чертёж и решают задачу. После того как задача решена, к ней составляются две обратные задачи.
(· Экскурсия вместе с дорогой в парк и обратно заняла 1 час. На дорогу было потрачено 20 минут. Сколько длилась экскурсия?
· Экскурсия вместе с дорогой в парк и обратно заняла 1 час. Экскурсия длилась 40 минут. Сколько времени было потрачено на дорогу?)
