Формула для плотностей. Условное распределение. Байесовское оценивание дисперсии нормального закона.
Теория:
Практика в R:
library("LearnBayes")
d <- (footballscores$favorite - footballscores$underdog) - footballscores$spread #наблюд. величина - прогноз
d.sd <- sd(d) #нашли реальное значение среднекв. отклонения
#hist(d)
#curve(dnorm(x,sd=d.sd), add=TRUE) #Должно работать, но нет
p = rchisq(1000,length(d))/sum(d^2)
s = sqrt(1/p) #оценка среднеквад. отклонения с помощью байессовского метода
mean(s)
[1] 13.87063
Односторонние и двухсторонние доверительные интервалы для случайной величины. Построение доверительных интервалов с помощью квантилей. Процедура построения в пакете R.
Теория:
Постановка задачи
Пусть случайная величина Х имеет функцию распределения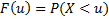 
.
Односторонние интервалы: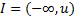 
– левый; 
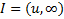– правый.
Двусторонний интервал: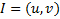 
.
Доверительная вероятность: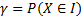 
.
Задача: по заданной доверительной вероятности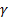 
требуется вычислить 
.
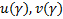Решение этой задачи находится через квантили распределения.
Квантиль распределения:
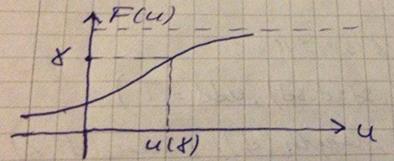
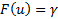– неявное уравнение. Требуется найти 
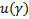– квантиль уровня .
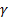Решение для односторонних интервалов
: 
: 
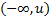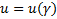
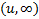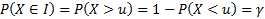
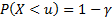
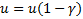
Решение для двусторонних интервалов
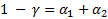
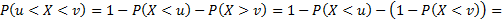
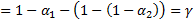
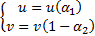
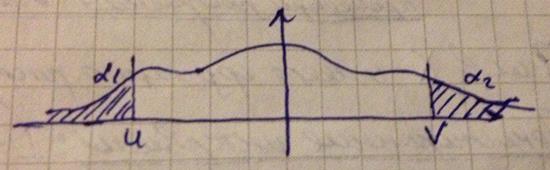
Практика:
q<имя распределения>(x) – поиск квантиля уровня x для конкретного распределения qnorm(x), qexp(x), …
Пример
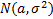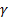, -фикс.
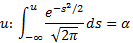
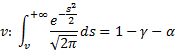
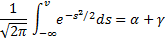
gm <- 0.9
f <- function(a) {
qnorm(gm + a, 0, 1) – qnorm(a, 0, 1)
}
curve(f, 0, 1 - gm)
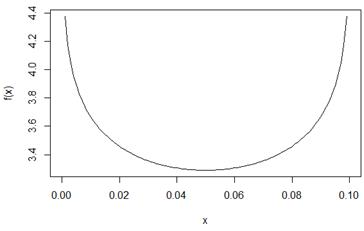
Пусть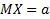 
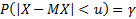
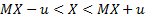
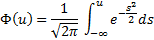
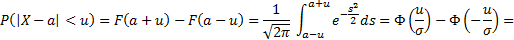
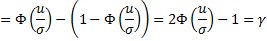
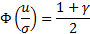
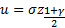
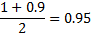
2*qnorm(0.95,0,1) # = 3.289707 – минимум функции на графике выше
Простые и сложные гипотезы. Ошибки первого и второго рода. Критерий согласия Колмогорова – Смирнова. Применение с критерия в пакете R.
Теория:
Гипотезы
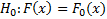– нулевая гипотеза
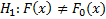– альтернативная гипотеза
Простая гипотеза – гипотеза, которой удовлетворяет только одно распределение вероятности
Сложная гипотеза – несколько распределений
Критерий согласия Колмогорова-Смирнова
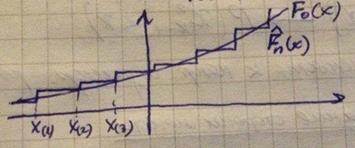
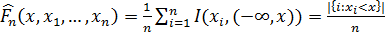– эмпирическая функция распределения
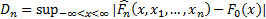– статистика Колмогорова-Смирнова
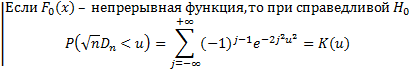
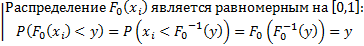
Независимо от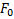 
, закон распределения 
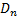такой, как если бы все 
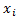имели бы равномерный на 
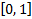закон распределения.
Если 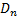малые, то 
.
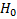Если 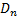большие, то 
.
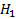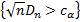– критическая область.
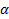– вероятность ошибки 1го рода (уровень значимости критерия).
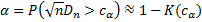
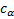– квантиль уровня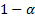 
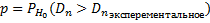– p-значение (p-value).
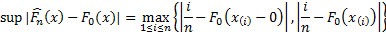
Практика:
Пример 1
Угадывание результатов подбрасывания монетки (10 бросков).
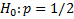– угадываем
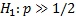– предсказываем
Множество возможных раз угаданных результатов: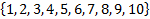 
Пусть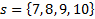 
– критическая область.
При попадании в критическую область отвергаем нулевую гипотезу. С помощью критической области можем управлять вероятностью ошибки.
Вероятность ошибки 1го рода: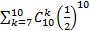 
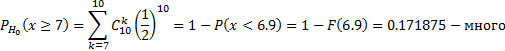
sum(dbinom(7:10,10,0.5)) или 1 - pbinom(6.9,10,0.5)
: 
: 
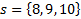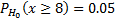
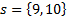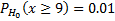
В данном примере ошибку 2го рода невозможно вычислить, так как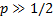 
(то есть не знаем точно значения)
Пример 2
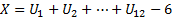
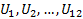– н.о.р. сл. вел. с равномерным на (0, 1) распределением.
На основании центральной предельной теоремы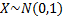 
.
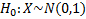
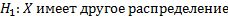
x <- replicate(100, sum(runif(12)) - 6)
qqnorm(x)
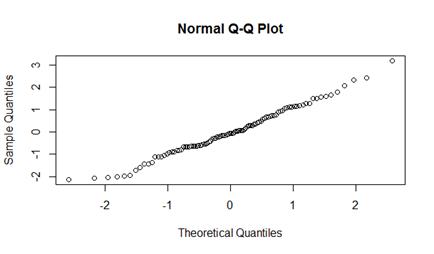
Проверка равномерности датчиков случайных чисел с помощью критерия Колмогорова-Смирнова:
ks.test(runif(100), punif, alternative =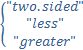 
)
Вывод: D = 0.06008, p-value = 0.8642