Графические методы представления и анализа данных: гистограммы, графики «ящик с усами», диаграммы рассеяния, матрицы диаграмм рассеяния. Использование цвета для выявления группировок

Теория:

Гистограмма:

Плотность распределения случайной величины :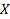

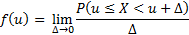
Мы хотим по имеющейся выборке 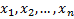случайной величины 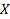построить оценку плотности распределения. Логично это сделать так:

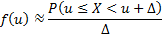
Вероятность 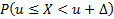тоже можно оценить по выборке, заменив эту вероятность частотой возникновения события :

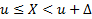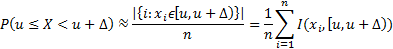
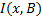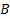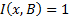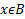Здесь – индикаторная функция (индикатор) множества . при и 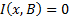иначе. Получаем:

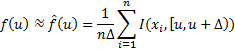
Если мы изобразим график 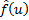, то получим ступенчатый график, пытающийся повторить форму графика истинной плотности 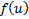. Его и называют гистограммой. Однако в таком виде гистограмма получается не очень наглядной. Лучше её строить так: разбиваем интересующий нас отрезок оси 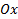(например, 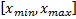) на 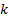интервалов 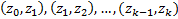и строим оценку плотности следующим образом:

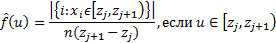
Разбиение можно строить, руководствуясь следующими правилами:

1) Просто разбиваем отрезок на равные части (число частей – по вкусу)

2) Разбиваем отрезок таким образом, чтобы в каждый интервал попало равное количество элементов выборки (число попаданий - по вкусу)

3) Правило Sturges’а: разбиваем отрезок на 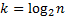частей. Используется обычно для нормального и биномиального распределений.

4) Правило Скотта: минимизируем мат. ожидание нормы ошибки (то есть величину 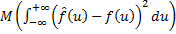), изменяя .

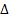5) Правило Фридмана-Диаконисса: 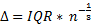. 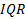(межквартильный размах) – длина размаха между третьим и первым квартилями выборки. То есть отсекаем от упорядоченной выборки первую четверть и последнюю четверть значений и считаем размах.

hist(x)

Cтроит гистограмму по выборке 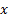(массив), используя правило Sturges’а, в абсолютных частотах (то есть без деления на )

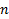hist(x, prob = T), hist(x, freq = F)

То же, но в относительных частотах (с делением на )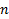

hist(x, breaks = z)

Строит гистограмму по заданному разбиению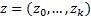

hist(x, breaks = k)

Строит гистограмму, разбивая отрезок на k равных частей

hist(x, “Sturges”), hist(x, “Scott”), hist(x, “FD”)

Строит гистограмму методами Sturges’а, Скотта и Фридмана-Диаконисса

Ящик с усами:

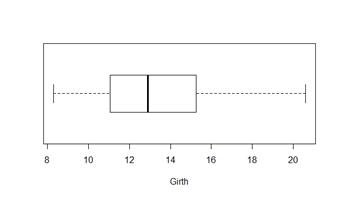
boxplot(x)

Рисует «ящик с усами» по выборке 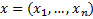. Границы ящика – первый и третий квартили (25% и 75% упорядоченной выборки). Полоса в ящике – медиана (50%). Усы включают в себя всё остальное, кроме выбросов. Выбросы рисуются отдельными точками. Как определяются выбросы, на лекции не рассказывалось.

Диаграмма рассеяния:

plot(y ~ x)

Строит диаграмму рассеяния для двумерной выборки 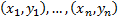. По сути, это просто координатная плоскость, на которой отмечены точки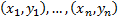

Матрица диаграмм рассеяния:

pairs(c(x, y, z, t, …))

Строит матрицу диаграмм сравнения, содержащую диаграммы рассеяния для всех попарных сочетаний переменных x, y, z, t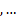

Практика в R:

func.hist <- function() {

#Для выбора интервалов для отображения гистограммы есть 3 метода: breaks = "Sturges", "Scott", "FD" либо вектор точек

#col - задает цвет

#hist также возвращает breaks, counts - абсолютные частоты, оценки плотности на интервалах в density

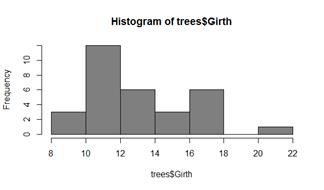
print(hist(trees$Girth,col="grey50",breaks="Sturges")) #print печатает все значения и рисует гистограмму

}

func.boxplot <- function() {

#ящик с усами

boxplot(trees$Girth,horizontal=TRUE, xlab="Girth");

}

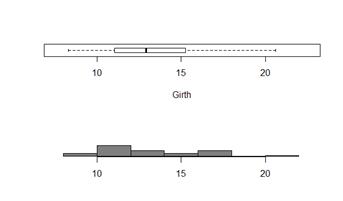
func.hist_and_boxplot <- function() {

par(mfrow=c(2,1)); #для отображения 2 графиков

par(mar = par("mar")*c(.8,1,1,1)); #отступы

boxplot(trees$Girth,horizontal=TRUE, xlab="Girth", ylim=range(trees$Girth)*c(0.9,1.1)); #ylime - отображать поменьше хотим

hist(trees$Girth,col="grey50", prob=TRUE, main="", axes=FALSE, xlab="", ylab="",xlim =range(trees$Girth)*c(0.9,1.1) );

axis(1) #отображаем ось по x (в теории можно и подписать)

}

func.pie <- function() {

x <- c("Yes", "Yes", "No", "Yes")

pie(table(x))

}

func.diagram_1 <- function() {

#Строим одномерную диаграмму рассеяния

stripchart(Sepal.Length ~ Sepal.Width, #по x, по y

xlab = "Длина",

ylab = "Ширина",

method = "stack") #способ отображения квадратиков, если совпало по x и y (либо друг над другом, либо только 1)

}

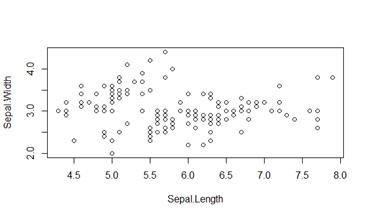
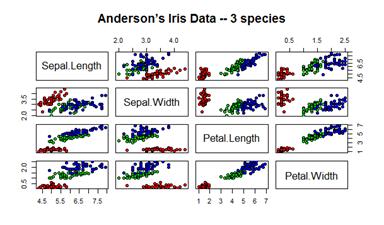
func.diagram_n <- function() {

pairs(iris[1:4], #т.к. хранится Sepal.Length,Width; Petal.Length,Width и Species, отрезаем так последнее

main = "Anderson’s Iris Data -- 3 species",

pch = 21, #специальный формат точечек, чтобы разноцветные были; 24 - треуг-ки, 21 - кружочки

bg = c("red", "green3", "blue")[Species]) #Назначаем каждому Species цвет - на выходе Species, только вместо Species, там цвета

}