Теплоотдача при свободном и вынужденном движении жидкости

Свободное движение жидкости происходит под действием разности плотностей нагретых и холодных частей жидкости. Эта разность температур зависит от разности температур теплообменной поверхности и жидкости. Форма поверхности имеет второстепенное значение, поэтому уравнение подобия для естественной конвекции имеет вид

.

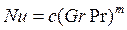Константы 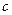и 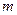зависят от режима движения жидкости, т.е. от произведения :

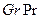для ламинарного режима ( 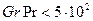) 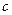=1,18, 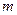=0,125;

для переходного режима ( 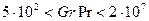) 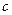=0,54, 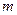=0,25;

для турбулентного режима ( 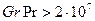) 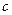=0,135, 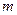=0,33.

В качестве определяющих геометрических размеров при вычислении чисел Грасгофа приняты: для цилиндрических или сферических тел – диаметр; для плоских поверхностей – высота.

В качестве определяющей температуры, т.е. температуры, при которой вычисляются значения физических параметров, входящих в критерии подобия, принята средняя температура пограничного слоя, равная 0,5( ).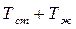

Теплоотдача при вынужденном движении жидкости. Интенсивность теплоотдачи при вынужденном движении жидкостей в первую очередь зависит от режима течения жидкости. Соответственно этому рассматривается теплоотдача в условиях установившегося турбулентного, ламинарного и переходного режимов течения жидкости.

В условиях установившегося турбулентного течения ( 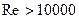) теплоотдача зависит от характера движения и свойств жидкости:

.

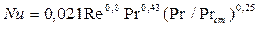Физические параметры в критериях 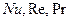определены при средней температуре жидкости, а в критерии 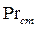при температуре стенки. Отношением критериев 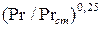учитывается влияние на теплоотдачу направления теплового потока и температурного перепада. Определяющим геометрическим размером принят эквивалентный диаметр канала, равный учетверенной площади поперечного сечения канала, деленной на смоченный периметр. Зависимость справедлива для случаев движения жидкости по прямым каналам любой формы поперечного сечения.

В коротких каналах коэффициент теплоотдачи выше, чем в длинных. Его величина снижается с увеличением 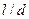от 1 до 50. Дальнейшее увеличение 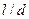не приводит к снижению коэффициента теплоотдачи. Если отношение 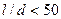, в критериальное уравнение вводится коэффициент 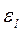, численные значения которого меняются в пределах от 1 до 1,65 в зависимости от 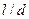и критерия Рейнольдса. Значение величины поправочного коэффициента 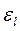можно найти в технической литературе.

При движении жидкости по изогнутой трубе или каналу с радиусом кривизны 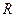теплообмен гораздо интенсивнее, чем при движении по прямому каналу. Увеличение интенсивности теплообмена в этом случае учитывается поправочным коэффициентом:

.

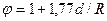В условиях ламинарного течения ( 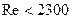) теплоотдача определяется как вынужденным, так и свободным движением жидкости.

На теплоотдачу при ламинарном режиме существенное влияние оказывает естественная циркуляция. В результате ее влияния коэффициент теплоотдачи иногда может изменяться в пять раз. Для горизонтальных круглых труб при расчете a может быть использована эмпирическая формула Михеева, учитывающая естественную конвекцию:

.

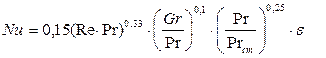Коэффициент e, учитывающий изменение коэффициента теплоотдачи в зависимости от длины трубы, указан в таблице:

l/d
e	1,9	1,7	1,44	1,28	1,18	1,13	1,05	1,02	1,00

При ламинарном режиме, когда влияние свободной конвекции невелико (Gr×Pr £5×10⁵ ), критериальные уравнения имеют вид:

при (Re×Pr×d/l >12) ;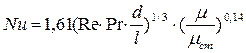

при (Re×Pr×d/l £12) ,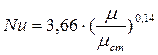

где m_ст, - коэффициент динамической вязкости теплоносителя принимается при температуре стенки.

Для расчета теплоотдачи при движении теплоносителя, не меняющего своего фазового состояния, по трубам и каналам при переходном режиме (10⁴>Re>2300) могут быть использованы зависимости:

.

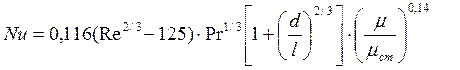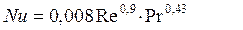(для P r= 20¸140)

Экспериментальные данные при поперечном обтекании труб и трубных пучков обобщаются в виде эмпирических уравнений:

для коридорного пучка

при 10< Re <150

;

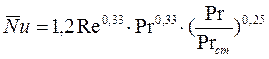при 10³< Re <10⁵

;

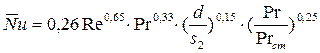для шахматного пучка

при 10< Re <200

;

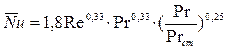при 10³< Re <10⁵

.

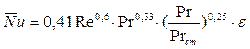При течении теплоносителя в межтрубном пространстве кожухотрубного теплообменника с сегментными перегородками могут быть использованы зависимости

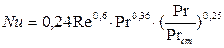(при Re ³10³),

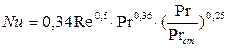(при Re <10³).

В них определяющую скорость потока рассчитывают для наименьшего сечения межтрубного пространства.