На использование формул для сочетаний
1.Сколькими способами из восьми человек можно избрать комиссию, состоящую из пяти членов?
Решение задачи:
Для решения этой задачи необходимо использовать формулу для сочетания элементов, т.к. здесь не имеет значения порядок элементов в выборке. Запишем формулу для сочетаний и произведем вычисления:
С 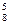 =
= 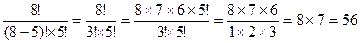 .
.
Ответ: 56.
2.Компания из двадцати мужчин разделяется на три группы, в первую из которых входят три человека, во вторую — пять и в третью — двенадцать. Сколькими способами они могут это сделать? (Ответ записать в виде произведения сомножителей, не вычисляя его.)
Решение задачи:
Из 20-ти элементов необходимо сделать три выборки, причем порядок внутри выборок значения не имеет. Поэтому используем формулу для сочетаний. Чтобы выбрать из 20-ти элементов 3, существует С 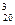 способов. Остается 17 элементов, из которых выбирается 5 элементов - С
способов. Остается 17 элементов, из которых выбирается 5 элементов - С 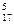 способами. Остается 12 элементов, из которых выбирается 12 элементов. Это можно сделать С
способами. Остается 12 элементов, из которых выбирается 12 элементов. Это можно сделать С 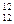 = 1, т.е. одним способом. Используя принцип произведения, получаем: С
= 1, т.е. одним способом. Используя принцип произведения, получаем: С 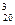
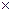 С
С 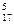
 С
С 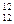 .
.
Ответ: С 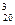
 С
С 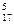
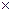 С
С 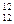 .
.
На использование формул для перестановок и сочетаний
1.Сколько четырехбуквенных слов можно образовать из букв слова сапфир? 2) Сколько среди них таких, которые не содержат буквы р? 3) Сколько таких, которые начинаются с буквы с и оканчиваются буквой р?
Решение задачи:
1. Из шести букв составляются четырехбуквенные слова, причем порядок букв важен для образования новых слов. Поэтому используется формула для размещений: А 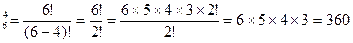 .
.
2. Необходимо исключить букву р из рассмотрения. Количество слов, не содержащих эту букву: А 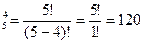 .
.
3. На первое место поставить букву с можно только одним способом. На последнее место поставить букву р можно тоже только одним способом. Остаются 4 буквы, которые необходимо разместить по двум местам: А 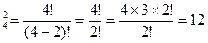 .
.
Ответ: 360, 120, 12.
2.Сколько пятибуквенных слов, каждое из которых состоит из трех согласных и двух гласных, можно. образовать из букв слова уравнение?
Решение задачи:
В слове уравнение 3 согласных и 4 гласных буквы русского алфавита. Чтобы посчитать количество требуемых пятибуквенных слов, необходимо посчитать количество сочетаний 3 согласных из 3-х заданных и двух гласных из четырех заданных: С 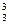 и С
и С 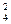 . После того, как 5 букв выбраны, необходимо посчитать все возможные перестановки этих букв: С
. После того, как 5 букв выбраны, необходимо посчитать все возможные перестановки этих букв: С 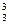
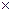 С
С 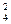
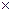 P5.
P5.
Ответ: С 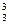
 С
С 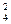
 P5.
P5.
Варианты заданий
Задача 1. Сколькими различными маршрутами можно разнести корреспонденцию в пять адресов. ( Маршрут определяется последовательностью адресатов)?
Задача 2.Цифры 0,1,2,3 написаны на четырех разноцветных карточках. Сколько различных четырехзначных чисел можно сложить из этих карточек?
Замечание. Первая цифра числа не может быть нулем. Карточку можно использовать в числе только один раз.
Задача 3.Вхоккейном турнире участвуют 6 команд. Каждая команда должна сыграет с каждой одну игру. Сколько игр сыграно в турнире?
Задача 4.Из трех классов спортивной школы нужно составить команду для соревнований, взяв по одномуученику от класса. Сколько различных команд можно составить, если в одном классе учатся 18, в другом 20, в третьем 22 ученика?
Задача 5.На плоскости задано множество A, состоящее из 8 точек. Три из них выкрашены в красный цвет и лежат на одной прямой, а остальные расположены так, что проходящая через пару точек прямая не содержит других точек множества. Через каждые две точки множества A проведено по прямой линии. Сколько всего прямых линий получилось?
Задача 6.Сколькими способами можно упорядочить множество 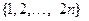 так чтобы каждое четное число имело четный номер?
так чтобы каждое четное число имело четный номер?
Задача 7.В ящике находится 20 деталей. Известно, что 5 из них являются стандартными. Из этих деталей выбирают 3. Сколько существует способов выбора трех деталей таких, чтобы среди них была, по крайней мере, одна стандартная?
Задача 8.Из 7 разноцветных карточек разрезной азбуки составлено слово колокол.Ребенок, не умеющий читать, случайно рассыпал эти карточки. Сколькими способами из этих карточек он сможет снова составить слово колокол?
Задача 9.Имеется прямоугольник, разбитый на клетки. По горизонтали n клеток, а по вертикали– m клеток. Можно двигаться только по сторонам клеток либо вправо, либо вверх. Сколько существует различных путей из левого нижнего угла в правый верхний угол?
Самостоятельная работа №3 Вычисление вероятностей событий по классической формуле определения вероятности
