Размещения (упорядоченные выборки).

Элементы комбинаторики

Принцип умножения

Пусть необходимо выполнить одно за другим одновременно r действий. Если первое действие можно вы­полнить n₁ способами, после чего второе - n₂ способами и т.д. до r - того действия, которое можно выполнить n_r спосо­бами, то все r действий вместе можно выполнить n₁, n₂…n_r способами.

Пример: Сколько существует двузначных чисел?

Способ 1: (принцип умножения)

Выбирается две цифры, поэтому r= 2. Первая цифра может быть любой, кроме 0. Потому n₁= 9. Вторая цифра может быть любой, т.е. n₂=10. итак двузначных чисел: n₁n₂=9 ^. 10=90.

Способ 2. (перо6ора)

10 20 30 ………..90

11 21 31 …………91 прямоугольная таблица 10 ^. 9=90

12 22 32 …………92

………………………….

19 29 39 ………...99

Пример: Бросают три игральные кости и наблюдают за числом очков, появившихся на каждой кости. Сколько различных исходов опы­та возможно?

Решение: Бросают три игральные кости, поэтому по принципу умножения r= 3, На выпавшей грани "первой" игральной кости может появить­ся одно очко, два очка, ... шесть очков. Поэтому n₁= 6. Анало­гично n₂= 6, n₃= 6. Итак, число всех исходов опыта n₁n₂n₃= 6 ^.6 ^.6=216.

Пример: Сколько существует нечетных трехзначных чисел?

Решение: По принципу умножения r = 3 ; n₁ = 9, т.к. первая цифра может быть любой, кроме 0; n₂ = 10, т. к. вторая цифра может быть любой ; n₃ = 5, т.к. третья цифра должна быть нечетной. Итак, всех возмож­ностей

n₁n₂n₃ =9 ^. 10 ^. 5=450.

Замечания к принципу умножения. Если на выполнение какого-ли­бо из r действий наложено ограничение, то подсчет удобнее начи­нать с выполнения именно этого действия.

Пример: В машине 7 мест, одно место водителя. Сколькими спо­собами могут сесть в машину 7 человек, если место водителя могут занять только трое из них?

Решение: По принципу умножения r = 7. Начнем с места водителя n₁ = 3, следующее место может занять любой из 6 оставшихся человек, т.е. n₂ = 6, следующее место может занять любой из 5 оставшихся человек и т.д. Поэтому n₃ = 5, n₄ = 4, n₅ = 3, n₆= 2, n₇ = 1.

Итак, всех возможностей: n₁ ∙n₂ ∙n₃∙ n₄∙ n₅∙n₆∙n₇ =3∙6∙5∙4∙3∙2∙1 = 2160.

Размещения (упорядоченные выборки).

Пусть А – множество, состоящее из элементов а₁, а₂,…, а_n.

Определение: Упорядоченные наборы, состоящие из r элементов множество А, будем называть размещениями из n элементов множества А по r элементов.

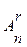– число размещений из n элементов по r элементов(r £n). Вычислим 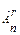по принципу умножения:

n₁₌ n,

n_{2 =}n-1, 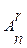₌ n(n-1)(n-2)….(n-r+1).

n_{3 =} n-2,

…………

n_r= n-(r-1) = n-r+1.

Здесь n, n-1, n-2,…,n-r+1 есть число возможностей для выбора первого, второго, третьего,… r – того элементов.

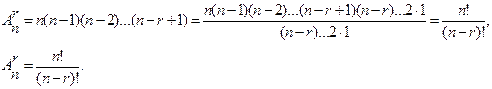
Перестановки

Определение: Размещения из n элементов по n элементов называются перестановки из n элементов.

P_n – число перестановок из n элементов.

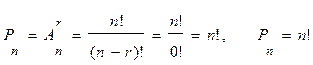
Пример: Сколькими способами могут 4 человека разместиться в 4-х местном купе железнодорожного вагона?

Решение: А = {1, 2, 3, 4} (4 места в купе вагона);

P₄ = 4! = 1∙2∙3∙4 = 24.

Варианты заданий

Решить комбинаторные уравнения

1.

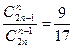
2.

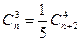
3.

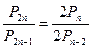
4.

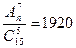
5.

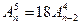
6.

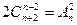
Самостоятельная работа №2 Расчет количества выборок заданного типа в заданных условиях

Задачи на расчет количества выборок

Варианты заданий

Задача 1. Сколькими различными маршрутами можно разнести корреспонденцию в пять адресов. ( Маршрут определяется последовательностью адресатов)?

Задача 2.Цифры 0,1,2,3 написаны на четырех разноцветных карточках. Сколько различных четырехзначных чисел можно сложить из этих карточек?

Замечание. Первая цифра числа не может быть нулем. Карточку можно использовать в числе только один раз.

Задача 3.Вхоккейном турнире участвуют 6 команд. Каждая команда должна сыграет с каждой одну игру. Сколько игр сыграно в турнире?

Задача 4.Из трех классов спортивной школы нужно составить команду для соревнований, взяв по одномуученику от класса. Сколько различных команд можно составить, если в одном классе учатся 18, в другом 20, в третьем 22 ученика?

Задача 5.На плоскости задано множество A, состоящее из 8 точек. Три из них выкрашены в красный цвет и лежат на одной прямой, а остальные расположены так, что проходящая через пару точек прямая не содержит других точек множества. Через каждые две точки множества A проведено по прямой линии. Сколько всего прямых линий получилось?

Задача 6.Сколькими способами можно упорядочить множество 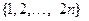так чтобы каждое четное число имело четный номер?

Задача 7.В ящике находится 20 деталей. Известно, что 5 из них являются стандартными. Из этих деталей выбирают 3. Сколько существует способов выбора трех деталей таких, чтобы среди них была, по крайней мере, одна стандартная?

Задача 8.Из 7 разноцветных карточек разрезной азбуки составлено слово колокол.Ребенок, не умеющий читать, случайно рассыпал эти карточки. Сколькими способами из этих карточек он сможет снова составить слово колокол?

Задача 9.Имеется прямоугольник, разбитый на клетки. По горизонтали n клеток, а по вертикали– m клеток. Можно двигаться только по сторонам клеток либо вправо, либо вверх. Сколько существует различных путей из левого нижнего угла в правый верхний угол?

Самостоятельная работа №3 Вычисление вероятностей событий по классической формуле определения вероятности

Варианты заданий

Решить задачи

1. Из ящика, в котором 10 белых и 6 черных шаров, берут наудачу 3 шара. Какова вероятность того, что один из них белый, а два черных?

2. Набирая номер телефона, абонент забыл три последние цифры, запомнив лишь, что они различные, набрал их наудачу. Найти вероятность того, что набраны нужные цифры?

3. 25 экзаменационных билетов содержат по две вопроса, которые не повторяются. Студент подготовил 45 вопросов. Какова вероятность того, что вытянутый студентом билет состоит из подготовленных им вопросов?

4. В мастерскую для ремонта поступило 15 телевизоров. Известно, что 6 из них нуждаются в общей регулировке. Мастер берет первые попавшиеся 5 телевизоров. Какова вероятность того, что 2 из них нуждаются в общей регулировке.

5. Из колоды в 52 карты берется наугад 4 карты. Найти вероятность того, что среди этих 4 карт будут представлены все четыре масти.

6. На полке в случайном порядке расставлено 40 книг, среди них находится трехтомник А.С.Пушкина. Некто взял наудачу с полки 5 книг. Найти вероятность того, что среди этих пяти книг есть трехтомник Пушкина.

7. Секретных замок содержит на общей оси 4 диска, каждый из которых разделен на 5 секторов с различными цифрами. Замок открывается только в том случае, если диски установлены так, что образуют определенное число. Найти вероятность того, что при произвольной установке дисков замок откроется.

Самостоятельная работа №4 Нахождение условных вероятностей. Вычисление вероятностей сложных событий с помощью теорем умножения и сложения вероятностей

1. Основные определения

Определение: Событие, которое в результате опыта должно произойти непременно, называется достоверным событием.

Определение: Событие, которое в данном опыте не может произойти, называется невозможным.

Вероятность достоверного события равна единице, вероятность невозможного события равна нулю.

Определение: Два события называют несовместными, если появление одного из них исключает появление другого в одном и том же испытании.

Определение: Суммой А+В двух событий А и В называется событие, состоящее в появлении хотя бы одного из них, т. е. или событие А или В или А и В вместе.

Определение: Произведением А^.В двух событий А и В называется событие, состоящее в совместном появлении события А и события В.

Определение: Противоположным к А называется событие 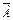, состоящее в том, что А не произошло.

Определение: Два события называются независимыми, если вероятность одного из них не зависит от появления или не появления другого.

Определение: Пусть А и В – зависимые события. Условной вероятностью Р(В|А) (или P_A(B)) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

Варианты заданий

Решить задачи

Самостоятельная работа №5 Вычисление вероятностей сложных событий с помощью формулы полной вероятности

Формула полной вероятности

Пусть событие А происходит совместно с одним из событий (гипотез) Н₁, Н₂,… Н_n, которые образуют полную группу событий. Тогда справедлива формула полной вероятности события А :

,

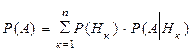где Р(Н_к) – вероятность гипотезы Н_к, Р(А½Н_к) – условная вероятность А, т.е. вероятность появления события А при условии, что произошла гипотеза Н_к .

Пример. Три автомата изготовляют одинаковые детали.

Известно, что первый автомат производит 30% всей продукции, второй – 25% и третий – 45%. Вероятность изготовления детали, соответствующей стандарту, на первом автомате равна 0,99, на втором – 0,988 и на третьем – 0,988. все изготовленные за смену детали складываются вместе. Определить вероятность того, что взятая наудачу деталь не соответствует стандарту.

Решение: Пусть событие А – взятая наудачу деталь не соответствует стандарту.

Гипотезы:

Н₁- взятая деталь изготовлена первым автоматом;

Н₂- взятая деталь изготовлена вторым автоматом;

Н₃- взятая деталь изготовлена третьим автоматом.

Вычислим вероятность гипотез.

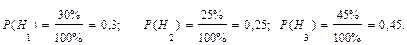
Вычислим условные вероятности:

Р(А½Н₁) – вероятность того, что взятая наудачу деталь не соответствует стандарту, если она изготовлена первым автоматом.

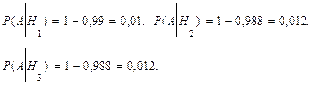
Вероятность события А подсчитываем по формуле полной вероятности :

Р(А)=0,3 ^.0,01+0,25 ^.0,012+0,45 ^.0,012=0,009.

Пример. В первой урне 7 белых и 3 черных шара, во второй – 8 белых и 2 черных. При перевозке из первой урны во вторую урну перекатились два шара. После того, как шары во второй урне перемешались, из неё выкатился шар. Найти вероятность того, что выкатившийся из второй урны шар белый.

Решение: Пусть событие Н₁ состоит в том, что из первой урны во вторую перекатились два белых шара, событие Н₂ состоит в том, что перекатились два чёрных шара, а событие Н₃ состоит в том, что перекатились шары разного цвета. Можно вычислить вероятности Р(Н₁) = 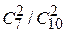= 7/15, Р(Н₂) = 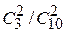= 1/15, Р(Н₃) = 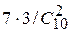= 7/15 (при решении задачи полезно проверить выполнение необходимого условия ).

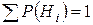Если реализовалась гипотеза Н₁, то во второй урне оказалось 10 белых и 2 черных шара. Обозначим через А событие, заключающееся в том, что из второй урны выкатился белый шар. Тогда Р(А/Н₁) = 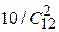= 5/33. Если реализовалась гипотеза Н₂, то во второй урне оказалось 8 белых и 4 чёрных шара, и Р(А/Н₂) = 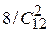= 4/33. Легко показать, что Р(А/Н₃) = 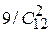= 3/22. Теперь можно воспользоваться формулой полной вероятности:

Р(А) = (5/33)×(7/15) + (4/33) (1/15) + (3/22) (7/15) = 47/330

Пример. В ящике лежат 20 теннисных мячей, в том числе 15 новых и 5 играных. Для игры выбираются 2 мяча и после игры возвращаются обратно. Затем для второй игры также наудачу извлекаются ещё два мяча. Найти вероятность того, что вторая игра будет проводиться новыми мячами.

Решение Обозначим через А событие, заключающееся в том, что вторая игра будет проводиться новыми мячами. Пусть гипотеза Н₁ состоит в том, что для первой игры были выбраны два новых мяча, гипотеза Н₂ состоит в том, что для первой игры были выбраны новый и играный мячи, гипотеза Н₃ состоит в том, что для первой игры были выбраны два играных мяча. Определим вероятности гипотез:

Р(Н₁) = 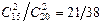; Р(Н₂) = 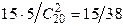; Р(Н₃) = .

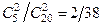Теперь вычислим условные вероятности события А.

Р(А/Н₁) = 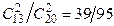; Р(А/Н₂) = 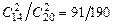; Р(А/Н₃) = .

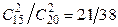Осталось подставить результаты вычислений в формулу полной вероятности

Р(А) = .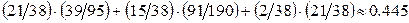

Пример.На автозавод поступили двигатели от трех моторных заводов. От первого завода поступило 10 двигателей, от второго – 6 и от третьего – 4 двигателя. Вероятности безотказной работы этих двигателей в течение гарантийного срока соответственно равны 0,9; 0,8; 0,7. Какова вероятность того, что установленный на машине двигатель будет работать без дефектов в течение гарантийного срока?

РешениеСобытие A – установленный на машине двигатель будет работать без дефектов в течение гарантийного срока – может произойти, если произойдет одно из несовместных событий: 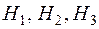– установленный на машине двигатель изготовлен на первом, втором или третьем заводе соответственно. Эти события образуют полную группу, их вероятности:

, , ,

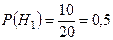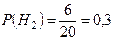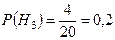(Контроль: ).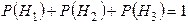

По условию , , .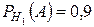

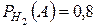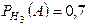По формуле полной вероятности

.

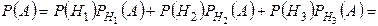
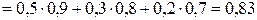Варианты заданий

Решить задачи

1. На фирме работают сотрудники разного возраста. Молодых сотрудников – 24, среднего возраста – 82 и пожилых – 16. Вероятность того, что молодого сотрудника отправят на повышение квалификации, равна 0,52; сотрудника среднего возраста – 0,54; пожилого – 0,36. Найдите вероятность того, что выбранного наудачу сотрудника отправят повышать квалификацию.

2. В библиотеке имеется 21 книга по истории, 34 книги –по математике, 25 книг – по юриспруденции. Вероятность того, что книга по истории занесена в электронный каталог, равна 0,33; по математике – 0,15; по юриспруденции – 0,61. Найдите вероятность того, что выбранная наудачу книга занесена в электронный каталог.

3. Пассажир за получение билета может обратиться в одну из трех касс. Вероятность обращения в первую кассу составляет 0,4, во вторую – 0,35, в третью – 0,25. Вероятность того, что к моменту прихода пассажира имеющиеся в кассе билеты будут проданы, равна для первой кассы 0,3, для второй – 0,4, для третьей – 0,6. Найти вероятность того, что пассажир купит билет.

Самостоятельная работа №6. Вычисление вероятностей сложных событий с помощью формулы полной вероятности и формулы Байеса. Подготовка сообщения «Практические приложения теории вероятностей»

Формула Байеса

Пусть вероятности гипотез до опыта были Р(Н₁), Р(Н₂),… Р(Н_n). В результате опыта появилось событие А . Тогда условная вероятность Р(Н_к½А) гипотезы Н_к с учетом появления события А вычисляется по формуле Байеса:

.

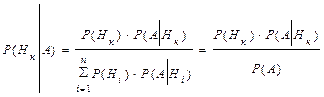Пример. На двух станках производят одинаковые детали, которые поступают на конвейер. Производительность первого станка в три раза больше производительности второго. Первый станок дает в среднем 80% деталей отличного качества, а второй –90%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того , что она изготовлена на втором станке.

Решение Пусть событие А - взятая наудачу с конвейера деталь отличного качества.

Гипотезы:

Н₁- деталь изготовлена на первом станке;

Н₂- деталь изготовлена на втором станке.

Вероятность гипотез до появления события А:

Р(Н₁)=3/4; Р(Н₂)=1/4.

Условные вероятности

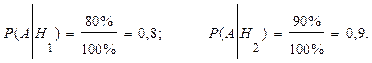
Вероятности того, что взятая наудачу с конвейера деталь окажется отличного качества, т.е. вероятность события А, вычисляется по формуле полной вероятности:

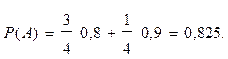
Искомая вероятность того, что взятая деталь отличного качества изготовлена на втором станке, вычисляется по формуле Байеса: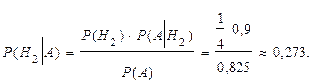

Пример. В первой урне 7 белых и 3 черных шара, во второй – 8 белых и 2 черных. При перевозке из первой урны во вторую урну перекатились два шара и шары во второй урне перемешались, из неё выкатился белый шар. Найти вероятность того, что из первой урны во вторую перекатились разноцветные шары.

Решение

Пусть событие Н₁ состоит в том, что из первой урны во вторую перекатились два белых шара, событие Н₂ состоит в том, что перекатились два чёрных шара, а событие Н₃ состоит в том, что перекатились шары разного цвета. Можно вычислить вероятности Р(Н₁) = 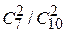= 7/15, Р(Н₂) = 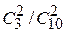= 1/15, Р(Н₃) = 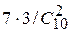= 7/15 (при решении задачи полезно проверить выполнение необходимого условия ).

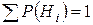Если реализовалась гипотеза Н₁, то во второй урне оказалось 10 белых и 2 черных шара. Обозначим через А событие, заключающееся в том, что из второй урны выкатился белый шар. Тогда Р(А/Н₁) = 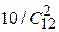= 5/33. Если реализовалась гипотеза Н₂, то во второй урне оказалось 8 белых и 4 чёрных шара, и Р(А/Н₂) = 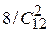= 4/33. Легко показать, что Р(А/Н₃) = 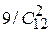= 3/22. Теперь можно воспользоваться формулой полной вероятности:

Р(А) = (5/33)×(7/15) + (4/33) (1/15) + (3/22) (7/15) = 47/330

Вычисления подставим в формулу Байеса

Р(Н₃/А) = Р(А/Н₃)Р(Н₃)/ Р(А) = (3/22)(7/15)/( 47/33) = 7/47.

Пример Сообщение со спутника на землю передаётся в виде бинарного кода, то есть как упорядоченного набора нулей и единиц. Предположим, что послание на 70% состоит из нулей. Помехи приводят к тому, что только 80% нулей и единиц правильно распознаются приёмником. Если принят сигнал “1”, то какова вероятность того, что отправлен сигнал “0”?

Решение Пусть событие В₀ состоит в том, что отправлен сигнал “0”, а событие В₁ – в том, что отправлен сигнал “1”. Пусть событие А₀ состоит в том, что принят сигнал “0”, с событие А₁ – в том, что принят сигнал “1”. Нас интересует Р(В₀/А₁). По условию

Р(В₀) = 0,7 Р(В₁) = 0,3

Р(А₀/ В₀) = 0,8 Р(А₁/ В₀) = 0,2

Р(А₁/В₀) = 0,8 Р(А₀/ В ₁) = 0,2

По формуле Байеса получаем

Р(В₀/А₁) = 0,2×0,7/(0,2×0,7+0,8×03) = 0,37.

Пример По цели независимо сбросили две бомбы.Вероятность попадания для каждой бомбы равна 1/2. При попадании одной бомбы цель поражается с вероятность 1/2, а при попадании двух бомб она поражается с вероятностью 2/3. Найти вероятность поражения цели.

Решение.Пусть события H₁, H₂ и H₃ состоят в попадании 0, 1 и 2 бомб соответственно. Событие A состоит в поражении цели. По формуле полной вероятности

P(A)=P(A|H₁)P(H₁)+ P(A|H₂)P(H₂)+ P(A|H₃)P(H₃).

P(A|H₁)=0, P(A|H₂)=1/2, P(A|H₃)=2/3, P(H₂)= ½, P(H₃)=1/4.

Поэтому, P(A)= (1/2)(1/2)+(2/3)(1/4)=5/12.

Варианты заданий

Решить задачи

1. В магазин поступают одинаковые электрические утюги: 80% с одного завода и 20% с другого. Известно, что первый завод выпускает 90% продукции, способной прослужить гарантийный срок, а второй завод – 95%. Какова вероятность, что купленный в магазине утюг прослужит гарантийный срок?

2. На сборку поступают изделия трех цехов: 50 изделий из первого цеха, 40 из второго и 30 из третьего. Вероятность того, что изделие первого цеха отличного качества, равна 0,8, для вто­рого цеха эта вероятность равна 0,9, для третьего - 0,8. Науда­чу взятое сборщиком изделие оказалось отличного качества. Какова вероятность, что это изделие поступило из второго цеха?

3. Известно, что в партии из 600 лампочек 200 лам­почек изготовлено первым заводом, 250 - вторым и 150 - третьим. Известно также, что вероятности изготовления стандартной лампоч­ки 1-м, 2-м и 3-м заводом соответственно равны 0,97 ; 0,91 ; 0,93. Какова вероятность того, что наудачу взятая из партии лам­почка окажется стандартной?

4. Трое охотников одновременно выстрелили по медведям, кото­рый был убит одной пулей. Определить вероятность того, что медведь был убит первым охотником, если вероятности попадания для них рав­ны соответственно: 0,2 ; 0,4 ; 0,6.

5. Была проведена одна и та же контрольная работа в трех параллельных группах. В 1-ой группе, где 30 учащихся, оказалось 8 работ, выполненных на «отлично»; во 20ой, где 28 учащихся – 6 работ, в 3-ей, где 27 учащихся – 9 работ. Найти вероятность того, что первая взятая наудачу при повторной проверке работа из работ, принадлежащих группе, которая также выбрана наудачу, окажется выполненной на «отлично».

6. В пирамиде 5 винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.

7. В вычислительной лаборатории имеется шесть клавишных автомата и четыре полуавтомата. Вероятность того, что за время выполнения некоторого расчета автомат не выйдет из строя, равна 0,95. для полуавтомата эта вероятность равна 0,8. Студент производит расчет на наудачу выбранной машине. Найти вероятность того, что до окончания расчета машина не выйдет из строя.

8. В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95. Для винтовки без оптического прицела 0,8. Стрелок поразил мишень их наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него?

Самостоятельная работа №7 Вычисление вероятностей сложных событий с помощью формулы Бернулли

Решение

а) Искомую вероятность находим с помощью формулы Бернулли (14), учитывая что , , , .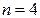

.

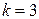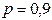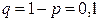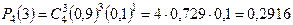б) «Не менее трех» означает, что из четырех семян взойдут или три, или четыре. Так как эти события несовместны, то по теореме сложения искомая вероятность равна

.

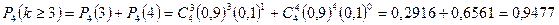Варианты заданий

Решить задачи

1. В магазин поступила партия лампочек, среди них 3 % составляет брак. Найти вероятность того, что из 5 купленных лампочек 4 будут хорошими.

2. Вероятность изготовления на автоматическом станке бракованной детали равна 0,1. Какова вероятность того, что из четырех деталей бракованных окажется не более двух?

3. При установившемся технологическом процессе автомат производит 0,75 числа деталей первого сорта и 0,25 – второго. Установить, что является более вероятным – получить 3 первосортных детали среди 5 наудачу отобранных или 4 первосортных среди 6 наудачу отобранных?

4. Среди изделий, произведенных а станке-автомате, в среднем бывает 90 % изделий первого сорта. Какова вероятность того, что среди 5 наудачу выбранных изделий будет не менее 4 первого сорта?

5. Что вероятнее: выиграть у равносильного противника не менее 3 партий из 4 или не менее 5 из 8?

6. Вероятность банкротства одной из 5 фирм к концу года равна 0,2. Какова вероятность того, что к концу года обанкротится не более двух фирм?

Приложение 1

Таблица значений интеграла Лапласа

x	Сотые доли х
	0,00000	0,00399	0,00798	0,01197	0,01595	0,01994	0,02392	0,02790	0,03188	0,03586
0,1	0,03983	0,04380	0,04776	0,05172	0,05567	0,05962	0,06356	0,06749	0,07142	0,07535
0,2	0,07926	0,08317	0,08706	0,09095	0,09483	0,09871	0,10257	0,10642	0,11026	0,11409
0,3	0,11791	0,12172	0,12552	0,12930	0,13307	0,13683	0,14058	0,14431	0,14803	0,15173
0,4	0,15542	0,15910	0,16276	0,16640	0,17003	0,17364	0,17724	0,18082	0,18439	0,18793
0,5	0,19146	0,19497	0,19847	0,20194	0,20540	0,20884	0,21226	0,21566	0,21904	0,22240
0,6	0,22575	0,22907	0,23237	0,23565	0,23891	0,24215	0,24537	0,24857	0,25175	0,25490
0,7	0,25804	0,26115	0,26424	0,26730	0,27035	0,27337	0,27637	0,27935	0,28230	0,28524
0,8	0,28814	0,29103	0,29389	0,29673	0,29955	0,30234	0,30511	0,30785	0,31057	0,31327
0,9	0,31594	0,31859	0,32121	0,32381	0,32639	0,32894	0,33147	0,33398	0,33646	0,33891
	0,34134	0,34375	0,34614	0,34849	0,35083	0,35314	0,35543	0,35769	0,35993	0,36214
1,1	0,36433	0,36650	0,36864	0,37076	0,37286	0,37493	0,37698	0,37900	0,38100	0,38298
1,2	0,38493	0,38686	0,38877	0,39065	0,39251	0,39435	0,39617	0,39796	0,39973	0,40147
1,3	0,40320	0,40490	0,40658	0,40824	0,40988	0,41149	0,41308	0,41466	0,41621	0,41774
1,4	0,41924	0,42073	0,42220	0,42364	0,42507	0,42647	0,42785	0,42922	0,43056	0,43189
1,5	0,43319	0,43448	0,43574	0,43699	0,43822	0,43943	0,44062	0,44179	0,44295	0,44408
1,6	0,44520	0,44630	0,44738	0,44845	0,44950	0,45053	0,45154	0,45254	0,45352	0,45449
1,7	0,45543	0,45637	0,45728	0,45818	0,45907	0,45994	0,46080	0,46164	0,46246	0,46327
1,8	0,46407	0,46485	0,46562	0,46638	0,46712	0,46784	0,46856	0,46926	0,46995	0,47062
1,9	0,47128	0,47193	0,47257	0,47320	0,47381	0,47441	0,47500	0,47558	0,47615	0,47670
	0,47725	0,47778	0,47831	0,47882	0,47932	0,47982	0,48030	0,48077	0,48124	0,48169
2,1	0,48214	0,48257	0,48300	0,48341	0,48382	0,48422	0,48461	0,48500	0,48537	0,48574
2,2	0,48610	0,48645	0,48679	0,48713	0,48745	0,48778	0,48809	0,48840	0,48870	0,48899
2,3	0,48928	0,48956	0,48983	0,49010	0,49036	0,49061	0,49086	0,49111	0,49134	0,49158
2,4	0,49180	0,49202	0,49224	0,49245	0,49266	0,49286	0,49305	0,49324	0,49343	0,49361
2,5	0,49379	0,49396	0,49413	0,49430	0,49446	0,49461	0,49477	0,49492	0,49506	0,49520
2,6	0,49534	0,49547	0,49560	0,49573	0,49585	0,49598	0,49609	0,49621	0,49632	0,49643
2,7	0,49653	0,49664	0,49674	0,49683	0,49693	0,49702	0,49711	0,49720	0,49728	0,49736
2,8	0,49744	0,49752	0,49760	0,49767	0,49774	0,49781	0,49788	0,49795	0,49801	0,49807
2,9	0,49813	0,49819	0,49825	0,49831	0,49836	0,49841	0,49846	0,49851	0,49856	0,49861
	0,49865	0,49869	0,49874	0,49878	0,49882	0,49886	0,49889	0,49893	0,49896	0,49900
3,1	0,49903	0,49906	0,49910	0,49913	0,49916	0,49918	0,49921	0,49924	0,49926	0,49929
3,2	0,49931	0,49934	0,49936	0,49938	0,49940	0,49942	0,49944	0,49946	0,49948	0,49950
3,3	0,49952	0,49953	0,49955	0,49957	0,49958	0,49960	0,49961	0,49962	0,49964	0,49965
3,4	0,49966	0,49968	0,49969	0,49970	0,49971	0,49972	0,49973	0,49974	0,49975	0,49976
3,5	0,49977	0,49978	0,49978	0,49979	0,49980	0,49981	0,49981	0,49982	0,49983	0,49983
3,6	0,49984	0,49985	0,49985	0,49986	0,49986	0,49987	0,49987	0,49988	0,49988	0,49989
3,7	0,49989	0,49990	0,49990	0,49990	0,49991	0,49991	0,49992	0,49992	0,49992	0,49992
3,8	0,49993	0,49993	0,49993	0,49994	0,49994	0,49994	0,49994	0,49995	0,49995	0,49995
3,9	0,49995	0,49995	0,49996	0,49996	0,49996	0,49996	0,49996	0,49996	0,49997	0,49997

Приложение 2

Таблица значений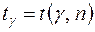

g n	0,95	0,99	0,999	g n	0,95	0,99	0,999
	2,78 2,57 2,45 2,37 2,31 2,26 2,23 2,20 2,18 2,16 2,15 2,13 2,12 2,11 2,10	4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,06 3,01 2,98 2,95 2,92 2,90 2,88	8,61 6,86 5,96 5,41 5,04 4,78 4,59 4,44 4,32 4,22 4,14 4,07 4,02 3,97 3,92	¥	2,093 2,064 2,045 2,032 2,023 2,016 2,009 2,001 1,996 1,991 1,987 1,984 1,980 1,960	2,861 2,797 2,756 2,720 2,708 2,692 2,679 2,662 2,649 2,640 2,633 2,627 2,617 2,576	3,883 3,745 3,659 3,600 3,558 3,527 3,502 3,464 3,439 3,418 3,403 3,392 3,374 3,291

Таблица значений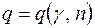

g n	0,95	0,99	0,999	g n	0,95	0,99	0,999
	1,37 1,09 0,92 0,80 0,71 0,65 0,59 0,55 0,52 0,48 0,46 0,44 0,42 0,40 0,39	2,,67 2,01 1,62 1,38 1,20 1,08 0,98 0,90 0,83 0,78 0,73 0,70 0,66 0,63 0,60	5,64 3,88 2,98 2,42 2,06 1,80 1,60 1,45 1,33 1,23 1,15 1,07 1,01 0,96 0,92		0,37 0,32 0,28 0,26 0,24 0,22 0,21 0,188 0,174 0,161 0,151 0,143 0,115 0,099 0,089	0,58 0,49 0,43 0,38 0,35 0,32 0,30 0,269 0,245 0,226 0,211 0,198 0,160 0,136 0,120	0,88 0,73 0,63 0,56 0,50 0,46 0,43 0,38 0,34 0,31 0,29 0,27 0,211 0,185 0,162

Приложение 3

Элементы комбинаторики

Принцип умножения

Пусть необходимо выполнить одно за другим одновременно r действий. Если первое действие можно вы­полнить n₁ способами, после чего второе - n₂ способами и т.д. до r - того действия, которое можно выполнить n_r спосо­бами, то все r действий вместе можно выполнить n₁, n₂…n_r способами.

Пример: Сколько существует двузначных чисел?

Способ 1: (принцип умножения)

Выбирается две цифры, поэтому r= 2. Первая цифра может быть любой, кроме 0. Потому n₁= 9. Вторая цифра может быть любой, т.е. n₂=10. итак двузначных чисел: n₁n₂=9 ^. 10=90.

Способ 2. (перо6ора)

10 20 30 ………..90

11 21 31 …………91 прямоугольная таблица 10 ^. 9=90

12 22 32 …………92

………………………….

19 29 39 ………...99

Пример: Бросают три игральные кости и наблюдают за числом очков, появившихся на каждой кости. Сколько различных исходов опы­та возможно?

Решение: Бросают три игральные кости, поэтому по принципу умножения r= 3, На выпавшей грани "первой" игральной кости может появить­ся одно очко, два очка, ... шесть очков. Поэтому n₁= 6. Анало­гично n₂= 6, n₃= 6. Итак, число всех исходов опыта n₁n₂n₃= 6 ^.6 ^.6=216.

Пример: Сколько существует нечетных трехзначных чисел?

Решение: По принципу умножения r = 3 ; n₁ = 9, т.к. первая цифра может быть любой, кроме 0; n₂ = 10, т. к. вторая цифра может быть любой ; n₃ = 5, т.к. третья цифра должна быть нечетной. Итак, всех возмож­ностей

n₁n₂n₃ =9 ^. 10 ^. 5=450.

Замечания к принципу умножения. Если на выполнение какого-ли­бо из r действий наложено ограничение, то подсчет