Дерево показателей достоверности диагноза
Эффективность – наиболее общая характеристика полезности технической системы, ее соответствие целевому назначению. Понятие эффективности относительно, т.к. при использовании одной и той же системы в разных условиях и для различных целей ее эффективность будет различной.
В процессе проектирования системы диагностирования на третьем этапе, после разработки диагностического обеспечения для проверки соответствия разработанной системы требованиям технического задания производят оценку эффективности.
Оценить эффективность системы диагностирования можно по величине вероятности правильной оценки состояния ОД или по мере повышения эффективности ОД, обусловленной применением системы диагностирования, с учетом затрат или потерь при ее использовании.
Процедура формирования показателя эффективности диагностирования в данном случае основана на построении иерархического дерева показателей. Показатели, находящиеся на разных уровнях дерева (рис.18.1), количественно характеризуют процесс функционирования системы диагностирования.
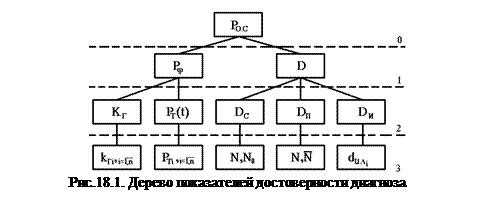
Показатель нулевого уровня представляет собой вероятность правильной оценки состояния объекта Ро.с и является критерием эффективности. На первом уровне расположены показатели, характеризующие надежность ТСД (вероятность правильного функционирования Рф, и достоверность диагноза D), на втором – частные показатели надежности ТСД (коэффициент готовности Кг, вероятность безотказной работы Рт(Т) на интервале времени Т) и составляющие достоверности диагностирования D (соответствие диагностической модели объекту Dс, полнота диагностирования Dп, инструментальная достоверность Dи), на третьем - показатели надежности структурных единиц, параметры диагностических признаков, показатели процесса диагностирования.
Вероятность Рф правильного функционирования ТСД при рабочем диагностировании определяют как коэффициент готовности Рф = Кг, который находят следующим образом.
Строят структурную схему надежности ТСД. Если схема представляет собой последовательное соединение СЕ, то
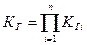 ,
,
где Кгi – коэффициент готовности i-й СЕ; n – число СЕ ТСД.
Если схема ТСД представляет собой параллельное соединение СЕ, то
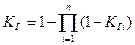
При тестовом диагностировании Рф = КгРт(Т).
Достоверность диагностирования D = DмDи.
Методическая достоверность Dм = DсDп.
Показатель соответствия диагностической модели объекту Dc = N/Nо,
где N – количество признаков, представляющих диагностическую модель; Nо – количество признаков представляющих ОД.
Показатель полноты диагностирования через число диагностических параметров N и измеряемых 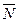 определяется:
определяется:
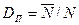 .
.
Инструментальную достоверность диагностирования Dи рассчитывают по формуле:
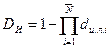 .
.
При определении Dи предполагают, что максимальная погрешность измерения  меньше поля допуска
меньше поля допуска 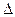 и случайные значения измеренной величины признака центрированные. Вероятность ложного значения dи.л.i по i-му диагностическому признаку
и случайные значения измеренной величины признака центрированные. Вероятность ложного значения dи.л.i по i-му диагностическому признаку
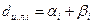 ,
,
где 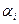 – вероятность того, что диагностический признак находится в допустимой области при получении заключения о выходе за пределы допустимой области;
– вероятность того, что диагностический признак находится в допустимой области при получении заключения о выходе за пределы допустимой области; 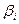 – вероятность того, что диагностический признак вышел за пределы допустимой области при получении заключения о нахождении признака в допустимой области.
– вероятность того, что диагностический признак вышел за пределы допустимой области при получении заключения о нахождении признака в допустимой области.
При расчете вероятностей 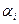 ,
, 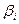 обычно рассматриваются соотношения между полем допуска
обычно рассматриваются соотношения между полем допуска 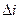 диагностических признаков, максимальным отклонением значений измерений hi от его математического ожидания и максимальной ошибкой измерения
диагностических признаков, максимальным отклонением значений измерений hi от его математического ожидания и максимальной ошибкой измерения 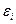 . Соотношения для определения
. Соотношения для определения 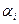 и
и 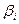 представлены в табл. 18.1.
представлены в табл. 18.1.
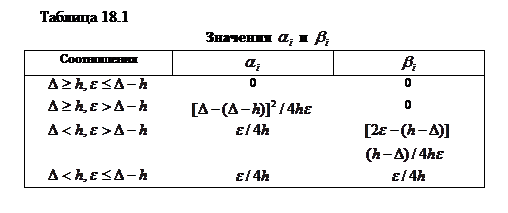
Значения hi и 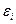 определяют из выражений
определяют из выражений 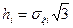 и
и 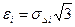 , где
, где 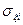 и
и 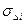 – среденеквадратичные отклонения диагностического признака и погрешности измерения от математического ожидания.
– среденеквадратичные отклонения диагностического признака и погрешности измерения от математического ожидания.
18.2. Расчет достоверности диагностирования с учетом
ошибок и сбоев в элементах системы
Вероятность правильного диагностирования определяется как полная вероятность того, что система диагностирования оценивает то состояние, в котором действительно находится объект диагностирования.
При этом следует иметь в виду, что возможны два исхода правильного диагностирования: положительный D – объект работоспособен (в объекте отсутствует дефект), отрицательный 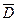 – объект не работоспособен (в объекте имеется дефект).Вероятности D и
– объект не работоспособен (в объекте имеется дефект).Вероятности D и 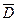 являются апостериорными вероятностями работоспособного и неработоспособного состояний ОД ирассчитываютсяпослезавершения разработки объекта и технических средств диагностирования.
являются апостериорными вероятностями работоспособного и неработоспособного состояний ОД ирассчитываютсяпослезавершения разработки объекта и технических средств диагностирования.
Причинами неправильной постановки диагноза могут быть:
неполный охват диагностированием объекта;
неидеальность технических средств в части их безотказности с учетом сбоев в их элементах;
неправильно выбранные соотношения между допусками на диагностические признаки 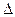 и погрешностями измерения
и погрешностями измерения  .
.
Полнота диагностирования определяется через вероятности обнаружения qо.о и необнаружения qн.о отказов, связанных соотношениями
qо.о + qн.о = 1 - Ро;
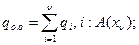
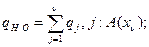
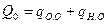
где qi – приведенная вероятность отказа ОД по вине i-го элемента; A( 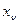 ) – предикат "дефект
) – предикат "дефект  -го элемента обнаруживается проверкой выбранной совокупности диагностических признаков"; Ро – вероятность безотказной работы ОД; Qо – вероятность отказа ОД.
-го элемента обнаруживается проверкой выбранной совокупности диагностических признаков"; Ро – вероятность безотказной работы ОД; Qо – вероятность отказа ОД.
Вследствие различной физической природы и сильной зависимости причин снижения достоверности от реальной структуры ТСД целесообразно выделить ошибки, возникающие из-за конечной безотказности составных элементов ТСД, и ошибки, возникающие из-за погрешности ТСД. Причем в первом случае ошибки являются следствием сбоев и устойчивых отказов составных элементов ТСД, а во втором случае определяются законами распределения, принятыми допусками оцениваемых признаков и погрешностями измерительной части ТСД.
Приведенные факторы имеют стохастическую природу, поэтому количественно оцениваются соответствующими вероятностными характеристиками.
Под сбоем принято понимать событие, которое приводит к неправильному функционированию технических средств, при этом работоспособность ТСД восстанавливается без вмешательства извне. Основными причинами сбоев служат внутренние и внешние помехи, разброс параметров элементов принципиальной схемы ТСД, а также их уход за границы допусков при изменении внешних условий. Обычно на практике для цифровых схем распределение сбоев подчиняется экспоненциальному, для аналоговых нормальному закону распределения.
Сбои можно охарактеризовать:
вероятностью сбоя, приводящего к ошибкам типа "ложный отказ" (событие h1): работоспособный объект признается неработоспособным (при отсутствии дефекта считается, что дефект возник)
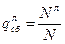 ,
,
где 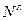 – количество сбоев опытного образца ТСД, приведших к ошибке типа ложный отказ; N – общее число испытаний работоспособного ОД при значительном увеличении допусков на проверяемые параметры;
– количество сбоев опытного образца ТСД, приведших к ошибке типа ложный отказ; N – общее число испытаний работоспособного ОД при значительном увеличении допусков на проверяемые параметры;
вероятность сбоя, приводящего к ошибке типа "необнаруженный отказ" (событие h2): отказавший объект признается работоспособным (при наличии дефекта считается, что дефект отсутствует)
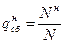
где 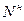 – количество сбоев опытного образца ТСД, приведших к ошибке типа необнаруженный отказ; N – общее число испытаний неработоспособного ОД при значительном уменьшении допусков на проверяемые параметры.
– количество сбоев опытного образца ТСД, приведших к ошибке типа необнаруженный отказ; N – общее число испытаний неработоспособного ОД при значительном уменьшении допусков на проверяемые параметры.
Отказы элементов могут приводить к полной потере работоспособности ТСД, либо они могут продолжать функционирование, но давать результаты диагностирования, не имеющие никакой связи с состоянием ОД. Последние отказы считаются неявными, и будет естественным учитывать их появление при расчете достоверности диагностирования.
Отказы можно охарактеризовать:
вероятностью того, что ТСД из-за возникших дефектов оценивают объект как работоспособный (событие h3):
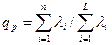 ,
,
где n – число элементов, отказы которых приводят к отмеченному событию (примером таких элементов может служить реле, обеспечивающее фиксацию конечного результата диагностирования); L – общее число элементов ТСД; 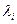 – интенсивность отказа i-го элемента;
– интенсивность отказа i-го элемента;
вероятностью того, что ТСД из-за возникших дефектов оценивают объект как неработоспособный (событие h4):
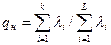 ,
,
где k – число элементов, отказы которых приводят к отмеченному событию.
Диагностирование предполагает выполнение целого ряда измерительных и контрольных операций, за счет погрешностей которых возможны ошибки первого и второго рода, определяемые соответственно вероятностью 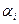 того, что i-й признак находится в допустимых пределах, но считается находящимся в недопустимых пределах, и вероятностью
того, что i-й признак находится в допустимых пределах, но считается находящимся в недопустимых пределах, и вероятностью 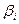 того, что i-й признак находится вне допустимых пределов, но считается находящимся в допустимых пределах при условии абсолютно надежных ТСД.
того, что i-й признак находится вне допустимых пределов, но считается находящимся в допустимых пределах при условии абсолютно надежных ТСД.
Вероятности 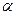 и
и  являются функциями
являются функциями 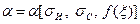 ,
, 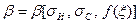 погрешности измерения
погрешности измерения 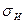 , сравнения
, сравнения 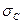 и законов
и законов 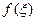 распределения значений диагностических признаков
распределения значений диагностических признаков 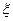 .
.
Когда состояние объекта определяется совокупностью из независимых признаков, ошибки можно оценить вероятностью ошибки первого рода 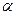 и вероятностью ошибки второго рода
и вероятностью ошибки второго рода  .
.
Вероятность 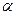 (событие h5) определяется следующим образом:
(событие h5) определяется следующим образом:
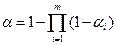 ,
,
где m – число признаков, контролируемых ТСД; 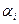 – вероятность ошибки первого рода по i-му признаку:
– вероятность ошибки первого рода по i-му признаку:
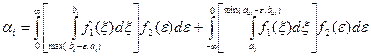 .
.
Здесь 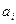 и
и 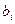 – соответственно нижняя и верхняя границы допуска на i-й признак;
– соответственно нижняя и верхняя границы допуска на i-й признак;  – погрешность измерения i-го признака;
– погрешность измерения i-го признака; 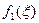 – плотность распределения значения измеряемого
– плотность распределения значения измеряемого 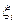 -го признака;
-го признака; 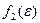 – плотность распределения погрешности
– плотность распределения погрешности  .
.
Вероятность  (событие h6) определяется следующим образом:
(событие h6) определяется следующим образом:
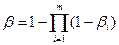 ,
,
где
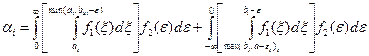 .
.
Рассмотрим возможность учета приведенных отказов, сбоев и ошибок при оценивании достоверности постановки правильного диагноза при положительном D и отрицательном 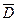 .
.
В процессе диагностирования объект может находиться в работоспособном (событие А) и неработоспособном (событие А) состояниях соответственно с вероятностями Ро и Qо. Состояние ОД оценивают технические средства диагностирования, которые перед применением или в процессе диагностирования работоспособны (событие В), либо перед применением или в процессе диагностирования в ТСД возникает отказ (сбой), приводящий к ошибочной оценке состояния ОД (событие В). Событие В может появиться вместе с любым из событий hi = 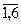 .
.
Обозначим через С и 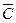 события, состоящие в признании ОД по результатам диагностирования соответственно работоспособным и неработоспособным. Причем события А и С,
события, состоящие в признании ОД по результатам диагностирования соответственно работоспособным и неработоспособным. Причем события А и С, 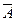 и
и 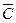 могут не совпадать в силу указанных выше причин. Такой подход позволяет формально разделить факторы, снижающие достоверность оценки состояния ОД, рассмотреть влияние каждого из них на достоверность получаемых от ТСД результатов диагностирования.
могут не совпадать в силу указанных выше причин. Такой подход позволяет формально разделить факторы, снижающие достоверность оценки состояния ОД, рассмотреть влияние каждого из них на достоверность получаемых от ТСД результатов диагностирования.
Тогда вероятности D и 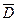 определяются по известным в теории вероятностей формулам Байеса:
определяются по известным в теории вероятностей формулам Байеса:
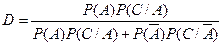 ; (18.1)
; (18.1)
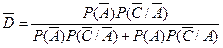 , (18.2)
, (18.2)
где P(A) и 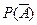 – безусловные вероятности событий А и
– безусловные вероятности событий А и 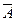 соответственно; P(C/A), P(C/
соответственно; P(C/A), P(C/ 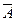 ), P(
), P( 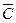 /A), P(
/A), P( 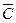 /
/ 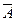 ) – условные вероятности соответствующих событий.
) – условные вероятности соответствующих событий.
Для определения условных вероятностей учтем, что события С и 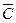 могут появиться с одним из следующих попарно несовместных событий, образующих полную группу:
могут появиться с одним из следующих попарно несовместных событий, образующих полную группу:
Н1 – достоверно событие А и В;
Н2 – достоверно событие А и 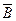 ;
;
Н3 – достоверно событие 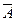 и В;
и В;
Н4 – достоверно событие 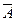 и
и 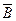 .
.
Тогда искомые условные вероятности гипотез могут быть определены с помощью выражений
Р(С/A) = Р(С/Н1) + Р(С/Н2) = Р(С1) + Р(С2); (18.3)
Р(С/ 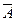 ) = Р(С/Н1) + Р(С/Н4) = Р(С3) + Р(С4); (18.4)
) = Р(С/Н1) + Р(С/Н4) = Р(С3) + Р(С4); (18.4)
Р( 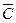 /A) = Р(
/A) = Р( 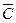 /Н1) + Р(
/Н1) + Р( 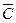 /Н2) = Р(
/Н2) = Р( 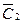 ); (18.5)
); (18.5)
Р( 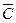 /
/ 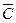 ) = Р(
) = Р( 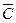 /Н3) + Р(
/Н3) + Р( 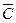 /Н4) = Р(
/Н4) = Р( 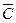 3) + Р(
3) + Р( 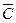 4). (18.6)
4). (18.6)
Вследствие того, что события 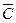 и Н1 несовместны и Р(
и Н1 несовместны и Р( 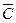 /Н1) = 0, то в выражение (18.5) входит лишь одно слагаемое.
/Н1) = 0, то в выражение (18.5) входит лишь одно слагаемое.
При количественной оценке достоверности получаемых от ТСД результатов практический интерес представляют два случая.
1. Часть отказов ТСД самоконтролем не обнаруживается (самоконтроль ограниченный).
2. Самоконтролем обнаруживаются все отказы ТСД (самоконтроль полный).
Рассмотрим каждый из возможных случаев отдельно.
Ограниченный самоконтроль. Требуется количественно оценить достоверность результатов положительного и отрицательного исходов диагностирования.
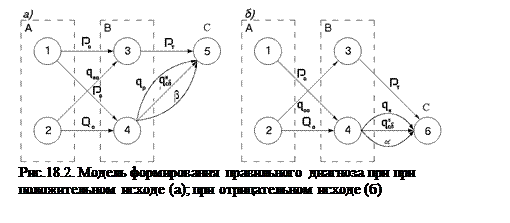
Для вычисления условных вероятностей, входящих в выражения (18.3)–(18.6), рассмотрим модель формирования диагноза в виде вероятностного ориентированного графа (рис.18.2). Вершины в графе соответствуют состоянию ОД, ТСД и системы в целом, а ветви характеризуются вероятностями нахождения элементов в указанных состояниях.
По вероятностному графу с учетом (18.3)–(18.6) определяем условные вероятности:
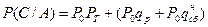 ;
;
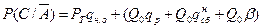 ;
;
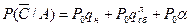 ;
;
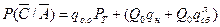 .
.
Используя выражения (18.1)–(18.2), с учетом полученного находим
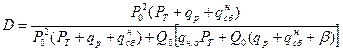 ; (18.7)
; (18.7)
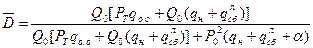 . (18.8)
. (18.8)
Из выражений (18.7), (18.8) видно, что достоверность диагностирования зависит не только от показателей инструментальной достоверности ( 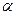 ,
,  ) и показателей надежности объекта и технических средств, но и от полноты диагностирования (qо.о, qн.о).
) и показателей надежности объекта и технических средств, но и от полноты диагностирования (qо.о, qн.о).
Полный самоконтроль. Пусть в ТСД отсутствуют и за время диагностирования не возникают отказы, т.е. qр=qн=0. При полном самоконтроле такое допущение оправдано. Действительно, если в ТСД имелся отказ до применения, то, вследствие полноты самоконтроля, он с вероятностью, близкой к единице, будет перед применением ТСД.
С другой стороны, т.к. время диагностирования значительно меньше времени наработки на отказ ТСД, то вероятность возникновения отказа за время диагностирования очень мала.
Действуя аналогично предыдущему, получим выражение для оценки достоверности диагностирования при полном самоконтроле:
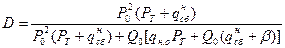 ;
;
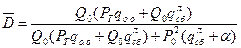 .
.
Полученные выражения для достоверности оценки работоспособного D и неработоспособного 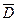 состояний позволяют при завершении создания СД оценить уровень разработки с учетом принятой инструментальной достоверности. Однако в этом случае не учитываются ошибки, сбои и отказы ЧО.
состояний позволяют при завершении создания СД оценить уровень разработки с учетом принятой инструментальной достоверности. Однако в этом случае не учитываются ошибки, сбои и отказы ЧО.
18.3. Повышение эффективности элементов ЭУ
Система диагностирования предназначена, главным образом, для повышения эффективности ОД. Поэтому оценивать эффективность целесообразно мерой повышения эффективности ЭУ с учетом затрат и потерь на использование системы диагностирования. Изменение эффективности ЭУ можно оценивать по абсолютной 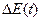 или относительной Е(t) величине изменения критерия эффективности, т.е.
или относительной Е(t) величине изменения критерия эффективности, т.е.
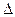 Е(t) = Фд(t) - Ф(t);
Е(t) = Фд(t) - Ф(t);
Е(t) = [Фд(t) - Ф(t)]/Ф(t),
где Ф(t) – показатель эффективности ЭУ без средств диагностирования; Фд(t) – показатель эффективности ЭУ при использовании средств диагностирования.
Следует заметить, что показатель эффективности содержит показатель надежности и в общем случае
Ф(t) = Фo(t)К(t),
где Фo(t) – составляющая эффективности, определяющая содержательную сторону процесса функционирования ЭУ ( например, количество производимой электроэнергии); К(t) – составляющая, характеризующая надежность ЭУ.
В связи с этим оценивать эффективность можно на основе расчета показателей надежности ЭУ с учетом влияния ТСД.
В качестве К(t) для ЭУ можно использовать показатель
К = (ТЭ-Тн)/Тэ,
где Тэ – рассматриваемый интервал времени эксплуатации ЭУ; Тн - время, когда ЭУ не используется по назначению.
В общем случае время Тн включает следующие составляющие:
Тн = То+Тв+ТТО+Тд,
где То – суммарное время неиспользования ЭУ по назначению из за отказов; Тв – суммарное время восстановления элементов ЭУ; ТТО – суммарное время технического обслуживания элементов ЭУ; Тд –суммарное время диагностирования элементов ЭУ.
Если ЭУ содержит несколько СЕ, то критерий эффективности каждой СЕ оценивается аналогично.
Смысловое значение показателя К определяют величины, входящие в Тн:
при Тн=То показатель К – вероятность Р(Тэ) безотказной работы ЭУ в интервале времени (0,Тэ);
при Тн=То + Тв показатель К – коэффициент Кг готовности ЭУ в интервале времени (0,Тэ);
при Тн=То+Тв+Тто показатель К – коэффициент технического использования Кт.и на интервале времени (0,Тэ);
при Тн=То+Тв+Тто+Тд показатель К – показатель Пг готовности ЭУ в интервале времени (0,Тэ).
То или иное смысловое значение показателя К выбирают на основе анализа условий эксплуатации элементов ЭУ, особенностей использования, содержания и организации диагностирования.
Контрольные вопросы
1. Какое смысловое значение имеет показатель К при Тн=То+Тв?
Ответы:
а) вероятность безотказной работы;
б) коэффициент готовности;
в) коэффициент технического использования;
2. Какое смысловое значение имеет показатель К при Тн = То+Тв+ТТО?
Ответы:
а) вероятность безотказной работы;
б) коэффициент технического использования;
в) показатель готовности.
3. Какое смысловое значение имеет показатель К при Тн = То?
Ответы:
а) вероятность безотказной работы;
б) коэффициент готовности;
в) показатель готовности.
4. Какими показателями определяется достоверность диагноза?
Ответы:
а) вероятностью правильного функционирования ТСД;
б) вероятностью безотказной работы;
в) соответствием диагностической модели объекту.
5. Какими показателями определяется вероятность правильного функционирования ТСД?
Ответы:
а) инструментальной достоверностью;
б) достоверностью диагноза;
в) коэффициентом готовности, вероятностью безотказной работы.
6. Какими показателями определяется вероятность правильной оценки состояния ОД ?
Ответы:
а) достоверностью диагноза, вероятностью правильного функционирования ТСД;
б) показателем готовности;
в) инструментальной достоверностью.
ЗАКЛЮЧЕНИЕ
Одним из путей поддержания высокой надежности элементов ЭУ в процессе длительной эксплуатации является диагностирование их состояния. Эту задачу можно решить на основе методов организации систем диагностирования, построения и анализа диагностических моделей, проектирования средств диагностирования, обеспечивающих высокую эффективность использования электроэнергетического оборудования.
Учитывая обстоятельство, что техническая диагностика служит инструментом поддержания надежности ЭУ в процессе эксплуатации, возникает необходимость ознакомления студентов с основами и методами расчета надежности, что изложено в первом разделе.
Во втором и третьем разделах рассмотрен материал по основам технической диагностики, методам и средствам диагностирования различных ЭУ, который нужен будущим инженерам-электрикам, специализирующимся в этой области.
Необходимость разработки перспективных и эффективных систем диагностирования элементов ЭУ определила изложение материала четвертого раздела как единой методологии системного проектирования на основе имеющихся достижений в области технической диагностики. Знакомство с современными методами решения задач проектирования систем диагностирования позволит реализовать новейшие результаты исследований в оптимальные конструктивные решения.
Авторы попытались представить по возможности полный материал по технической диагностике электрооборудования и линий электропередачи систем электроснабжения, проанализировав литературные источники в этой области. Недостающий материал по общим вопросам технической диагностики можно почерпнуть из приведенного списка литературы.
СПИСОК ЛИТЕРАТУРЫ
1. Бажанов С.А., Воскресенский В.Ф. Профилактические испытания изоляции оборудования высокого напряжения. М.:Энергия, 1977.
2. Балаков Ю.Н., Шевченко А.Т., Шунтов А.В. Надежность схем выдачи мощности электростанций/ Под. ред. А.Т. Шевченко. М.: Изд-во МЭИ, 1993
3. Вентцель Е.С. Теория вероятностей. М.: Наука, 1969.
4. ГОСТ 27.002-83. Надежность в технике. Термины и определения. М.: Изд-во стандартов, 1983.
5. ГОСТ 27518-87. Диагностирование изделий. Общие требования. М.: Изд-во стандартов, 1988.
6. ГОСТ 20911-89. Техническая диагностика. Термины и определения. М.: Изд-во стандартов, 1990.
7. Гук.Ю.Б. Анализ надежности электроэнергетических установок. Л.: Энергоатомиздат, 1989.
8. Гуляев В.А., Констанди Г.Г. Техническая диагностика. Методы определения периодичности диагностирования электроэнергетических систем. Киев:Техника, 1987.
9. Калявин В.П., Мозгалевский А.В., Галка В.Л. Надежность и техническая диагностика судового электрооборудования и автоматики: Учебник. СПб.: Элмор, 1996.
10. Правила технической эксплуатации электрических сетей и станций Российской Федерации/ 15-е изд. М.: М-во топлива и энергетики, 1996.
11. Розанов М.Н. Надежность электроэнергетических систем. 2-е изд. перераб. и доп. М.:Энергоатомиздат, 1984.
12. Рыбаков Л.М., Халилов Ф.Х. Повышение надежности работы трансформаторов и электродвигателей высокого напряжения. Иркутск: Изд-во Иркут. ун-та, 1991.
13. Сви П.М. Методы и средства диагностики оборудования высокого напряжения. М.: Энергоатомиздат, 1992.
14. Соколов В.В. Вопросы оценки обеспечения надежности силовых трансформаторов. //Изд. АН. СССР. Сер. Энергетика и транспорт, 1980.
15. Техника высоких напряжений: Учебник для студентов электротехнических и электроэнергетических вузов /Под. общ.ред. Д.В.Разевича.– 2-е изд, перераб. и доп. М: Энергия, 1976.
16. Техника высоких напряжений: Изоляция и перенапряжения в электрических системах: Учебник для вузов / Под общ. ред. В.П.Ларионова.– 3-е изд., перераб. и доп. М: Энергоатомиздат, 1986.
17. Ушаков В.Я. Старение изоляции и методы контроля ее состояния: Учебное пособие. Томск: Изд-во ТПУ, 1993.
18. Фокин Ю.А. Надежность и эффективность сетей электрических систем М.: Высшая школа, 1989.
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ3
ВВЕДЕНИЕ4
