Динамические наклонения судна

Прямая задача: определить угол крена при действии заданного динамического момента (М_{кр д}).

Допустим, что к судну приложен динамически постоянный по величине кренящий момент (М_{кр д}). Работа этого момента выражается линейной зависимостью 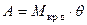, которую можно представить в виде 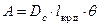, где D_с – вес судна, l_{кр д} – плечо кренящего момента, а θ – угол, измеряемый в радианах. Работу можно привести к единице силы веса судна: 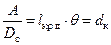, где d_к – удельная (приведенная) работа кренящего момента.

Удельная работа (d_кр, м∙рад.), также как и работа момента (А, кН∙м∙рад) выражается линейной зависимостью от угла крена.

Наличие зависимости 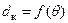позволяет «войти» в диаграмму 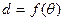(рис. 3.17) и решить рассматриваемую задачу. Для этого на оси абсцисс отмечается угол θ = 57,3° (1 радиан) и, с учетом того, что при θ = 1 радиан 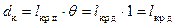, по вертикали откладывается отрезок равный, в масштабе оси ординат, значению 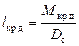. Затем через начало координат и верхний конец отрезка l_{кр д} проводится прямая, которая представляет собой зависимость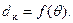

Искомый динамический угол крена (θ_д) определяется по точке пересечения зависимосте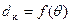й и 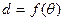; при θ_д имеет место равенство работ кренящего и восстанавливающего моментов.

Обратная задача: определить динамически приложенный постоянный по величине кренящий момент по известному значению угла (θ_д).

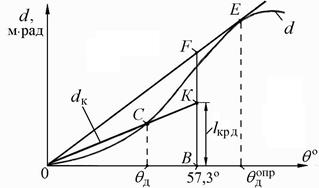Рис. 3.17. К решению основных задач по диаграмме

динамической остойчивости

С использованием диаграммы 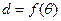(см. рис. 3.17) задача решается следующим образом. На графике проводятся вертикали при заданном значении угла (θ_д) – до кривой d (т. С) и при θ = 57,3° (1 радиан). Затем, из начала координат через точку С до пересечения с вертикалью при θ = 1 радиану (т. К) проводится прямая.

Отрезок ВК в масштабе шкалы ординат диаграммы определяет величину плеча (l_крд) искомого кренящего момента .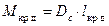

Третья задача: определить наибольший динамически приложенный кренящий момент ( 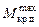), который может выдержать судно не опрокидываясь.

Для решения задачи обратимся к рис. 3.17. Нетрудно понять что, кренящий момент с плечом l_{кр д}, работа которого доводит судно до угла крена θ_д не является опрокидывающим; увеличивая момент кренящий будем получать все более крутые прямые (зависимости 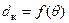, пересекающие диаграмму 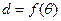при углах θ > θ_д.

Очевидно, что наиболее крутой прямой, имеющей общую точку с зависимостью 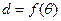, будет касательная к кривой d, которая и определяет искомое значение плеча 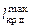и момента .

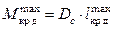Плечо 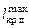находится как ордината касательной при угле 1 радиан (отрезок FB), а абсцисса точки касания (т. Е) определяет наибольший динамический угол крена .

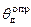Библиографический список

1. Сизов, В.Г. Теория корабля : учеб. / В.Г. Сизов. – 4-е изд., перераб. и дополн. – М. : ТрансЛит, 2008. – 464 с.

2. Перси Х.Дж. Остойчивость морского судна (пер. с англ. Д.Д. Соколова). – СПб. : ООО «МОРСАР», 2007, – 200 с.

3. Кеслер, А.А. Теория и устройство судна. Ч.1. Геометрия корпуса и плавучесть судна : учеб. пособие / А.А. Кеслер. – Н. Новгород : Изд-во ФБОУ ВПО «ВГАВТ», 2012. – 68 с.

4. Алферьев, М.Я. Теория корабля / М.Я. Алферьев. – 2-е изд., перераб. и дополн. – М. : Транспорт, 1972, – 448 с.

5. Благовещенский, С.Н. Справочник по статике и динамике корабля. В 2-х томах. Изд. 2-е, перераб. и доп. Т.1 Статика корабля / С.Н. Благовещенский, А.Н. Холодилин. Л. : Судостроение, 1975. – 336 с.

6. Осокин, М.В.Обеспечение мореходных качеств судна при составлении грузового плана : справ. пособие. / М.В. Осокин. – Н. Новгород : Изд-во ФБОУ ВПО «ВГАВТ», 2012. – 44 с.

7. Статика корабля: учеб. пособие / Р.В. Борисов, В.В. Луговский, Б.В. Мирохин, В.В. Рожденственский. – 2-е изд., перераб. и доп. СПБ. : Судостроение, 2005. – 256 с.

8. Жинкин, В.Б. Теория и устройство корабля : – 3-е изд., стереотип. – СПб. Судостроение, 2002. – 336 с.

ПРИЛОЖЕНИЕ

Таблица обозначений показателей по плавучести