Метацентрические высоты. Коэффициенты остойчивости

При наклонении судна из положения равновесия сила веса и сила плавучести образует пару сил. Момент, создаваемый парой сил (рис. 2.7) называется восстанавливающим моментом и может быть определен по формуле

Мq = Dc × lq	–	при поперечном наклонении;
Мy = Dc× ly	–	при продольном наклонении.

где	Dc	–	вес судна;
	lq, ly	–	плечо восстанавливающего момента (плечо статической остойчивости).

Восстанавливающий момент М_q,М_y (рис. 2.7) стремится вернуть судно в начальное положение. Это будет в том случае, если метацентры (m₀, М₀) находятся выше центра тяжести судна (G). В этом случае судно считается остойчивым. Если метацентр находится ниже центра тяжести судна или эти центры совпадают, судно считается неостойчивым.

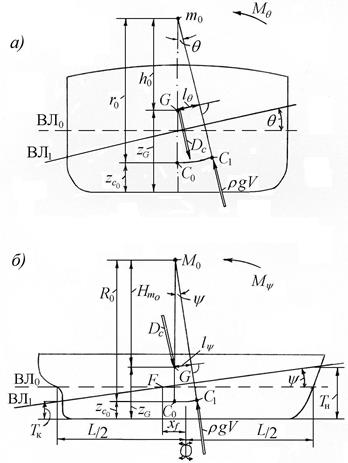Рис. 2.7. К выводу метацентрических формул остойчивости

Возвышение поперечного метацентра над центром тяжести называется начальной поперечной метацентрической высотой (h₀, рис. 2.7, а). Она может быть вычислена, если известны положение центра тяжести, центра величины и значение начального метацентрического радиуса, по формуле

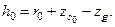(2.5)

Выражая восстанавливающий момент через начальную метацентрическую высоту, можно получить так называемую метацентрическую формулу остойчивости при крене

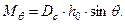
Эта формула дает достаточно точные в практических расчетах результаты при равнообъемных наклонениях в пределах малых углов.

Рассматривая равнообъемное наклонение в продольной плоскости, (рис. 2.7, б) нетрудно получить зависимость для начальной продольной метацентрической высоты

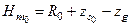(2.6)

и, по аналогии, получить метацентрическую формулу остойчивости при дифференте

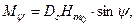(2.7)

где	Мy	–	восстанавливающий момент при дифферентовке;
	y	–	угол дифферента.

В формулы (2.5), (2.6) входят величины двоякого рода. Показатели R₀, r_0, 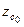определяются формой корпуса. При проектировании судна они вычисляются по теоретическому чертежу и изображаются на диаграмме элементов теоретического чертежа (рис. 2.8).

Аппликата центра тяжести судна (z_g) рассчитывается в таблице нагрузки по составленному грузовому плану для судна.

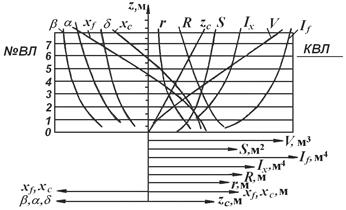Рис. 2.8. Кривые элементов теоретического чертежа*)

У судов с обычными обводами малый метацентрический радиус (r₀) в несколько десятков раз меньше большого метацентрического радиуса (R₀). Это свидетельствует о том, что у судов с удлиненной формой корпуса продольная остойчивость во много раз превышает их поперечную остойчивость.

Возникновению моментов, возвращающих судно в первоначальное положение после наклонения, соответствуют положительные значения метацентрических высот 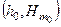; иначе говоря, судно обладает положительной остойчивостью только при услови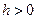и: и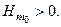

Средние значения поперечной метацентрической высоты для судов различных типов находятся в пределах (м):

сухогрузные суда……………………………..	0,4–1,5
танкеры………………………………………..	1,0–2,5
ледоколы……………………………………….	1,5–2,5
лесовозы……………………………………….	0,15–1,0
морские пассажирские суда………………….	1,0–1,8
пассажирские суда прибрежного плавания…	0,6–1,0
суда спасатели…………………………………	0,8–1,0

Удобным средством для оперативной оценки начальной остойчивости некоторого судна при изменении его нагрузки (массы судна) является диаграмма метацентрических высот. Она строится в прямоугольных координатах: по горизонтальной оси показывается массовое водоизмещение судна (D, т), а по вертикальной – статический момент (М_z, т×м) массового водоизмещения относительно горизонтальной плоскости. На поле диаграммы дается семейство кривых h_i = const (подробнее см. [1]).

Для быстрого решения вопроса о положении судна при крене удобно использовать момент, кренящий судно на 1°. Исходя из того, что при равновесном состоянии наклоненного судна кренящий и восстанавливающий моменты равны, момент, кренящий на 1°, можно определить следующим образом

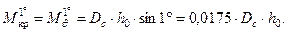
Тогда при действии на судно произвольного кренящего момента (М_кр) угол крена находится по формуле

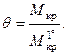
Формула (2.7) может быть использована для получения выражения удельного дифферентующего момента, т.е. момента создающего дифферент судна в 1 см. Для этого, с учетом малости углов дифферента (y для большинства судов не превышает 5°), в формуле (2.7) выполним замену: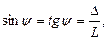

где	D=Тн – Тк	–	дифферент судна;
	L	–	длина судна.

С учетом замены формула (7) принимает вид 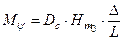. Задавшись значением D = 1 см можно получить зависимость для момента, создающего дифферент на 1 см (0,01 м)

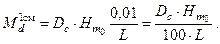
Если к судну приложен некоторый дифферентующий момент (М_d) и известен момент, дифферентующий на 1см ( 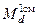) то вычисление дифферента сводится к расчету отношения моментов

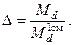
Количественным критерием, который может быть использован для сравнения начальной остойчивости различных судов и для одного и того же судна, при изменении водоизмещения, но при равных углах наклонения, является коэффициент остойчивости.

Коэффициент поперечной остойчивости (малый коэффициент остойчивости)

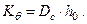
Коэффициент продольной остойчивости (большой коэффициент остойчивости)

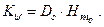
В отличие от момента восстанавливающего коэффициент остойчивости при нулевом угле наклонения не обращается в ноль.