Перемещение центра величины при малом равнообъемном наклонении. Метацентры и метацентрические радиусы

При равнообъемных наклонениях, как уже было отмечено, величина погружного объема остается неизменной, но меняется его форма. В силу последнего изменяется положение центра величины (рис. 2.4); он переместится из точки C₀ в точку C₁ по дуге .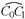

Прямая, соединяющая C₀ и C₁ ( 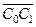) при малом равнообъемном наклонении на угол dq, будет параллельна и пропорциональна перемещению центра тяжести объемов dV, т.е.

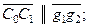
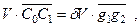
или, с учетом того, что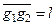

можно записать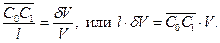

(2.2)

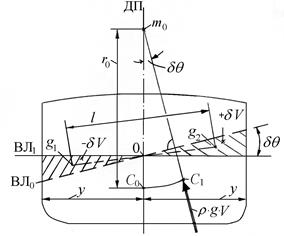Рис. 2.4. К определению поперечного метацентрического радиуса

Каждый из центров тяжести объемов -dV и +dV (на рис. 2.4 см. точки g₁, g₂) лежит на расстоянии 2/3 медианы от вершины треугольника – точки 0 (треугольники заштрихованы). Заменяя, ввиду малости угла dq, медиану стороной треугольника, лежащей в плоскости ватерлинии ВЛ₀, используя для dV выражение (1.1) и интегрируя по всей длине судна, получим

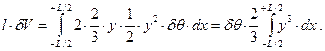Выражение 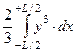представляет собой момент инерции (I_x) площади начальной ватерлинии относительно продольной оси, проходящей через центр тяжести площади. В самом деле, из рис. 2.5 видно, что элементарный момент относительно указанной оси для площадки длиной dx будет равен

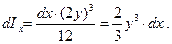
В соответствии с этим

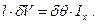(2.3)

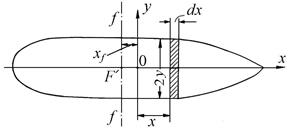Рис. 2.5. К определению момента инерции площади ватерлинии

Приравняв правые части соотношений (2.2) и (2.3) получим 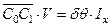или

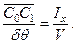(2.4)

Обратимся к рис. 2.4 и проведем через точку C₁ прямую перпендикулярную к ватерлинии ВЛ₁. Эта прямая при точке m₀ образует с диаметральной плоскостью (ДП) угол dq. Для плоской фигуры 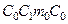, ввиду малости угла dq, справедливо соотношение 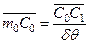. Точку m₀ называют начальный поперечный метацентр, а отрезок 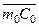– начальный поперечный метацентрический радиус (r₀).

С учетом формулы (2.4) можно записать 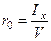, т.е. начальный метацентрический радиус при крене равен отношению момента инерции площади ватерлинии относительно продольной оси к объемному водоизмещению.

Метацентрический радиус при равнообъемных наклонениях остается постоянным по величине, а метацентр не меняет своего местоположения относительно судна, если значение центрального момента инерции площади ватерлинии относительно оси, перпендикулярной плоскости наклонения, постоянно.

Последнее имеет место, например, при наклонении на различные углы погруженного объема, имеющего форму правильного цилиндра, у которого ось симметрии параллельна поверхности воды.

При дифференте наклонение происходит вокруг поперечной оси, проходящей через центр тяжести площади действующей ватерлинии.

Путем аналогичных выкладок для продольного метацентрического радиуса может быть получена формула

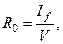
где

If

–

момент инерции площади ватерлинии относительно поперечной оси, проходящей через ее центр тяжести (т. F, рис. 2.5).

Момент инерции рассчитывается по формуле

,

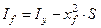где	Iy	–	момент инерции площади ватерлинии относительно оси 0Y;
	s	–	площадь ватерлинии;
	хf	–	отстояние центра тяжести площади S от миделя.

В соответствии с рис. 2.5 величину момента инерции элементарной площадки ватерлинии относительно поперечной оси можно представить в виде

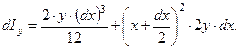
Пренебрегая значением собственного момента инерции площадки, а также и величиной 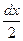по сравнению с х, можно получить момент инерции для всей площади ватерлинии

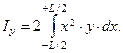
Радиус R называется большим или продольным метацентрическим радиусом, а соответствующий центр кривизны – продольным метацентром М₀ (рис. 2.6).

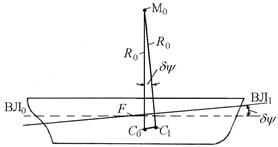Рис. 2.6. Продольный метацентр и продольный

метацентрический радиус

Из полученных выражений для определения r и R следует, что при равнообъемных наклонениях (V = const) метацентрический радиус, в общем случае, зависит от момента инерции площади ватерлинии (I_x или I_f).

Применительно к малым углам наклонения от начального (q = 0, y = 0) принимается допущение: 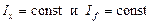. Вследствие этого, при малых равнообъемных наклонениях, кривая по которой перемещается центр величины как в поперечной, так и в продольной вертикальной плоскостях, является дугой окружности с центром в точке m₀ (рис. 2.4) и точке М₀ (рис. 2.6).

отмеченное позволяет получить простые зависимости для решения многих задач по остойчивости с достаточной для практики точностью.

В расчетах по остойчивости судна возможны случаи, когда ватерлиния имеет форму геометрической фигуры, для которой известны точные выражения моментов инерции ее площади. В табл. 2.1 приведены зависимости для центрального момента инерции площади фигуры относительно оси «у–у» и момента инерции относительно оси «а–а».

Таблица 2.1