Автокорреляция уровней временного ряда
Для анализа временных рядов применяется метод корреляционногоанализа.
Важной особенностью временных рядов по сравнению с данными наблюдений, относящихся к одному периоду времени, является, как правило, наличие связи между последовательными уровнями ряда, вызванное действием каких-либо долговременных причин. Это приводит к наличию таких составляющих ряда, как долговременная тенденция и периодическая составляющая.
При наличии тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих значений. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.
Количественно ее можно измерить с помощью линейного коэффициента автокорреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени:
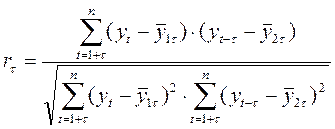 , где
, где 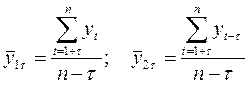
τ - величина сдвига, называемая лагом, определяет порядок коэффициента автокорреляции.
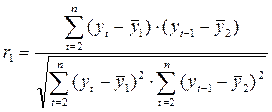 - коэффициент автокорреляции уровней ряда первого порядка, где
- коэффициент автокорреляции уровней ряда первого порядка, где 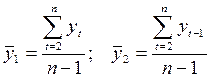 ;
;
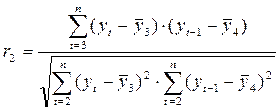 - коэффициент автокорреляции уровней ряда второго порядка, где
- коэффициент автокорреляции уровней ряда второго порядка, где 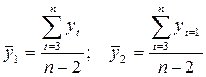 .
.
С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Некоторые авторы считают целесообразным для обеспечения статистической достоверности коэффициентов автокорреляции использовать правило «максимальный лаг должен быть не больше n/4».
Функцию r(τ) = rτ называют автокорреляционной функцией временного ряда, а ее график - коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет выявить структуру ряда, т. е. определить присутствие в ряде той или иной компоненты.
Так, если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит только тенденцию.
Если наиболее высоким оказался коэффициент автокорреляции порядка m, то ряд содержит циклические колебания с периодичностью в m моментов времени.
Если ни один из коэффициентов автокорреляции не является значимым, можно сделать предположение относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний и присутствуют только случайные колебания, либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компоненты Т и циклической (сезонной) компоненты S.
Необходимо подчеркнуть, что линейные коэффициенты автокорреляции характеризуют тесноту только линейной связи текущего и предыдущих уровней ряда. Поэтому по коэффициентам автокорреляции можно судить только о наличии или отсутствии линейной (или близкой к линейной) зависимости. Для проверки ряда на наличие нелинейной тенденции рекомендуется вычислить линейные коэффициенты автокорреляции для временного ряда, состоящего из логарифмов исходных уровней. Отличные от нуля значения коэффициентов автокорреляции будут свидетельствовать о наличии нелинейной тенденции.
3. Моделирование тенденции (тренда) временного ряда
Моделирование тенденции временного ряда является важнейшей классической задачей анализа экономических временных рядов.
