Метод неопределенных коэффициентов.

Этот метод рекомендуют применять при решении линейных дифференциальных уравнений с переменными коэффициентами. Суть метода покажем на примере уравнения второго порядка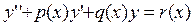

с начальными условиями 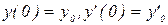. Предположим, что каждый из коэффициентов уравнения можно разложить в ряд по степеням x:

, , .

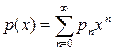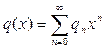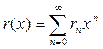Решение данного уравнения будем искать в виде ряда

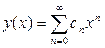, (9.3)

где 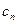- коэффициенты, подлежащие определению.

Дифференцируем обе части равенства (9.3) два раза по x:

, .

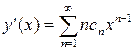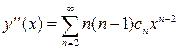Подставляя полученные ряды для 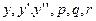в уравнение 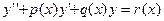, получим:

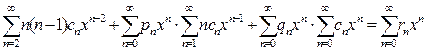. (9.4)

Произведя умножение рядов и приравняв коэффициенты при одинаковых степенях x в левой и в правой частях тождества (9.4), получим систему

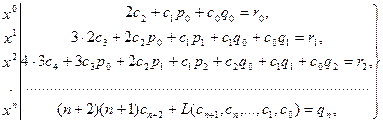(9.5)

где 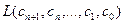означает линейную функцию аргументов .

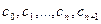Каждое уравнение системы (9.5) содержит на одно неизвестное больше по сравнению с предыдущим уравнением. Коэффициенты 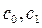определяются из начальных условий, а все остальные последовательно определяются из системы (9.5). Доказано, что если ряды 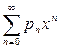, , 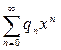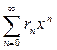сходятся при 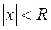, то полученный степенной ряд сходится в той же области и является решением уравнения

.

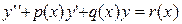Пример 9.4 Найти решение уравнения 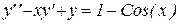с начальными условиями 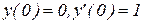в виде степенного ряда. Ограничиться 6 членами ряда.

Разложим коэффициенты уравнения в соответствующие степенные ряды.

p(x)=-x q(x)=-1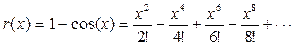

Будем искать решение уравнения в виде ряда

y=c₀+c₁x+c₂x²+ c₃x³+ c₄x⁴+…+c_nxⁿ+… тогда

y^'=c₁+2c₂x+3c₃x²+4c₄x³+…+n c_nx^n-1+…

-y^'x=-c₁x-2c₂x²-3c₃x³-4c₄x⁴-…- n c_nxⁿ+…

y^''=2c₂+6c₃x+12c₄x²+20c₅x³+…+n(n-1) c_nx^n-2+…

Подставив полученные ряды в уравнение примера, и приравняв коэффициенты при одинаковых степенях, получим систему для определения c_i .

c₀=0, c₁=1 возьмем из начальных условий.

x⁰ c₀ + 2 c₂ = 0,

x¹ 6 c₃ = 0,

x² – c₂ + 12 c₄ = ,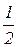

x³ – 2 c₃ + 20 c₅ = 0,

x⁴ – 3 c₄ + 30 c₆ = ,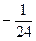

x⁵ – 4 c₅ + 42 c₇ = 0,

x⁶ – 5 c₆ + 56 c₈ = .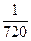

Решая последовательно систему, получим, что нечетные коэффициенты нули, а

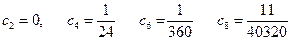
Приближенное решение задачи получаем в виде

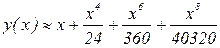
Численные методы

Метод Эйлера

Рассмотрим дифференциальное уравнение

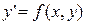(9.6)

с начальным условием 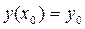. Выбрав достаточно малый шаг h, построим систему равноотстоящих точек .

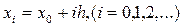В методе Эйлера приближенные значения 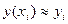вычисляются по формулам 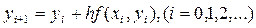. При этом искомая интегральная кривая 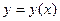, проходящая через точку 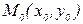, заменяется ломанной 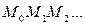с вершинами 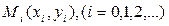; каждое звено 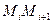этой ломанной, имеет направление той интегральной кривой уравнения 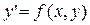, которая проходит через точку .

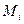Если правая часть уравнения 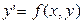в некотором замкнутом прямоугольнике 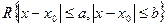удовлетворяет условиям

,

,

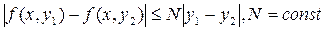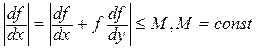то имеет место следующая оценка погрешности:

,

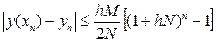где 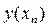- значение точного решения уравнения при 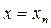, а 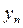- приближенное значение, полученное на n-м шаге в этой же точке.

На практике, для оценки точности полученных результатов, применяют двойной пересчет: расчет повторяют с шагом 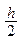и погрешность более точного значения 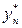в точке 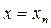оценивают приближенно так:

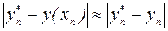
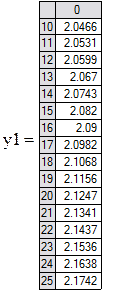
Пример 9.5. Используя метод Эйлера, составить таблицу приближенных значений решения дифференциального уравнения 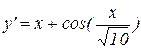с начальным условием y(0)=2 на отрезке [0;0.5] с шагом h с точностью до трёх знаков. Выполним это задание в Mathcad

Для этого разделим промежуток [a,b] на n частей и найдем шаг интегрирования h.

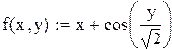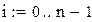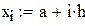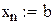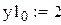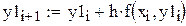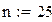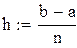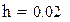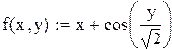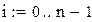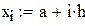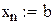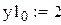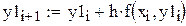Разделим промежуток интегрирования на 2n частей и

пересчитаем значения y_i с новым шагом h/2

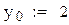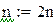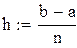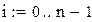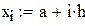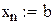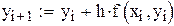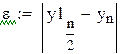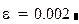
Решением уравнения является таблица значений у_i , найденных в точках отрезка [0;0.5] с шагом h=0,01 с точностью до трёх знаков.

Рис 9.1 Решение примера 9.5 в Mathcad методом Эйлера