Суммирование элементов. Вычисление минимального и максимального элемента
Определены следующие функции суммирования элементов массивов:
| Matlab | Scilab |
| sum(A) — возвращает сумму элементов массива, если А — вектор, или вектор-строку, содержащую сумму элементов каждого столбца, если А — матрица | sum(A [,fl]) - вычисляет сумму элементов массива X, имеет необязательный параметр fl. Если параметр fl отсутствует, то функция sum(A) возвращает скалярное значение, равное сумме элементов массива. Если fl=’r’, то функция вернет строку, равную поэлементной сумме столбцов матрицы A. Если fl=’с’, то результатом работы функции будет вектор-столбец, каждый элемент которого равен сумме элементов строк матрицы A. |
| max (A) — возвращает максимальный элемент массива, если А — вектор, или вектор-строку, содержащую максимальный элемент каждого столбца, если А — матрица | max(A [,fl]) - вычисляет наибольший элемент в массиве A, имеет необязательный параметр fl (аналогично функции sum) |
| min (A) — возвращает минимальный элемент массива, если А — вектор, или вектор-строку, содержащую минимальный элемент каждого столбца, если А — матрица | min(A [,fl]) - вычисляет наименьший элемент в массиве A, работает аналогично функции max |
Определитель матрицы
Для нахождения определителя (детерминанта) матриц имеются следующие функции:
· det(X) — возвращает определитель квадратной матрицы X.
Обращение матриц — функции inv, pinv
Обращение матриц — одна из наиболее распространенных операций матричного анализа. Обратной называют матрицу, получаемую в результате деления единичной матрицы Е на исходную матрицу X. Таким образом, Х-1 = Е/Х. Следующие функции обеспечивают реализацию данной операции:
· inv(X) — возвращает матрицу, обратную квадратной матрице X.
На практике вычисление явной обратной матрицы не так уж необходимо. Чаще операцию обращения применяют при решении системы линейных уравнений вида Ах=b. Один из путей решения этой системы — вычисление x=inv(A)*b. Но лучшим с точки зрения минимизации времени расчета и повышения точности вычислений является использование оператора матричного деления х=А\b. Эта операция использует метод исключения Гаусса без явного формирования обратной матрицы.
· В = pinv(A) — возвращает матрицу, псевдообратную матрице А (псевдообращение матрицы по Муру-Пенроузу). Результатом псевдообращения матрицы по Муру-Пенроузу является матрица В того же размера, что и А', и удовлетворяющая условиям А*В*А=А и В*А*В=В.
Определение размерности матриц
· [row, col] = size(A) – функция размерности матрицы A, возвращает количество строк row, и столбцов col.
Построение графиков функций в Matlab и Scilab
Построение графиков
Для построения графиков функций одной переменной y = f(x) имеется функция plot. График строится в декартовой системе координат по заданным массивам значений аргумента и функции. Заданные этими массивами точки соединяются прямыми линиями. Имеется возможность изменять тип и цвет линии и тип узловых точек (маркер). Вызов этой функции осуществляется командой:
plot(x,y,s)
в случае, если необходимо построить один график, или
plot(x1, y1, s1, x2, y2, s2, x3, y3, s3...xn, yn, sn)
для n графиков.
где x, y - одномерные массивы одинаковой размерности; x - массив значений аргумента функции у = f(x; y - массив значений функции у = f(x; s - строковая константа, определяющая цвет линии, маркер узловых точек и тип линии. Эта константа может содержать от одного до трех символов.
Строка s выглядит следующим образом
'параметр1параметр2параметр3'.
Символы пишутся один за другим без разделителей.
Параметр1 определяет цвет линии графика:
Значения параметра функции plot, определяющего цвет графика
| Символ | Описание | Символ | Описание |
| y | желтый | g | зеленый |
| m | розовый | b | синий |
| с | голубой | w | белый |
| r | красный | k | черный |
Параметр2 определяет тип маркера графика:
Значение параметра, определяющего тип маркеров (точек) графика
| Символ | Описание |
| . | точка |
| o | кружок |
| х | крестик |
| + | знак "плюс" |
| * | звездочка |
| S | квадрат |
| d | ромб |
| v | треугольник вершиной вниз |
| ^ | треугольник вершиной вверх |
| < | треугольник вершиной влево |
| > | треугольник вершиной вправо |
| p | пятиконечная звезда |
| h | шестиконечная звезда |
Параметр 3 определяет тип линии графика:
Значения параметра, определяющего тип линии графика
| Символ | Описание | Символ | Описание |
| - | сплошная | -. | штрихпунктирная |
| : | пунктирная | -- | штриховая |
Пример Matlab
% графики функций sin x, cos x
x=0:0.1:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,'k-o',x,y2,'r--*')
В результате выполнения этой программы на экран монитора будет выведено графическое окно с графиками, представленными на рис. 1.1. Графики представлены в черно-белой палитре, хотя в действительности график функции cos(x) выводится красным цветом.
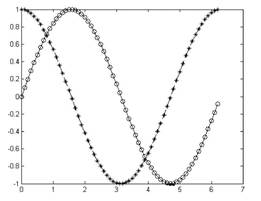
Рис. 1.1. Графики, выполненные с помощью программы plot
