Анализ систем с произвольным законом распределения времени обслуживания

Здесь мы будем рассматривать системы массового обслуживания с немарковским распределением времени обслуживания. Для входных потоков марковость будет сохранена. В качестве типичной СМО рассмотрим M/G/1.

Обозначим функцию распределения промежутков времени между последовательными поступлениями заявок на входе системы A (t).

По определению марковского процесса

.

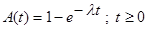Значение λ определяет интенсивность потока заявок, среднее значения промежутка времени между требованиями 1/λ, а дисперсия промежутка равна:

.

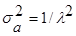Обозначим функцию распределения времени обслуживания B(x), а плотность распределения b(x).

Рассмотрим теперь описание СМО с точки зрения ее состояния в момент t. Обозначим N(t) число требований, присутствующих в системе в этот момент. Кроме того, необходимо знать время обслуживания, которое к данному моменту получило требование уже находящееся в сервере. Обозначим его X₀(t). Таким образом, от однокомпонентного описания состояния СМО с марковским процессом обслуживания для произвольного закона обслуживания необходимо перейти к двухкомпонентному описанию. Кроме дискретной составляющей N(t), теперь нужно рассматривать пару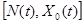

Где вторая компонента есть непрерывная функция. Для упрощения решения задачи будем рассматривать только специально выбранные моменты времени, для которых величина времени уже проведенного заявкой в сервере является величиной известной или еще лучше постоянной. Используемый здесь подход состоит в том, чтобы рассматривать исключительно моменты ухода заявок из системы и описывать состояние числом требований, остающихся в эти моменты в системе. На множестве точек на оси времени, определяемых этими моментами, построим вложенную марковскую цепь, как число требований, остающихся после ухода. Можно убедиться, что при этом получается полное описание состояний. Введем обозначения:

C_n – n-ое требование, поступающее в систему; τ_n - время поступления n-го требования, а t_n=τ_n-τ_n-1 = x_n – время обслуживания n-го требования.

Обозначим q_n – число требований, остающихся в системе в момент ухода требования C_n , а число требований, поступающих в систему за время обслуживания этого требования – v_n.

Найдем распределение вероятностей q_n , которое фактически зависит от времени. Предельное распределение, которое мы ранее называли p_k, есть не что иное как предел этого распределения при n→∞.

Марковская цепь описывается вероятностями перехода. Определим вероятности перехода за один шаг .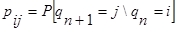

Матрица переходов будет иметь вид:

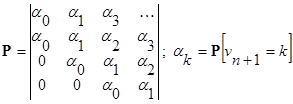
Например, j-элемент первой строки матрицы представляет собой вероятность того, что предыдущее требование, уходя, оставило систему пустой, а за время обслуживания требования C_n+1 поступает ровно j новых требований и все они остаются в системе после ухода требования C_n+1. Точно так же в других строках элемент p_ij при j > i-1 представляет собой вероятность поступления точно j-i+1 требований за время обслуживания n+1 требования при условии, что n-ое требование, уходя, оставляет в системе точно i требований. Диаграмма вероятностей переходов приведена на рис 3.1.

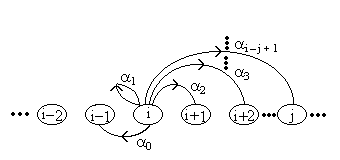
Рис. 3.1 Диаграмма вероятностей переходов для вложенной марковской цепи типаM/G/1.

Вычислим теперь значения α_k. Исходя из того, что входной поток пуассоновский и не зависит от состояния СМО, а также время обслуживания каждого требования также не зависит от состояния, отбросим индексы у обозначений соответствующих величин. По формуле полной вероятности будем иметь

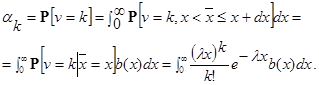
Эта формула полностью представляет матрицу перехода.

Все значения α положительны, что означает достижимость и неприводимость рассматриваемой марковской цепи. Введем обычное определение .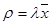

Если ρ<1, марковская цепь будет эргодична. В этом предположении можно получить матричное уравнение для определения стационарных вероятностей p_k , т.е. вероятностей того, что уходящее требование оставляет в СМО ровно k требований: 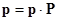, где вектор .

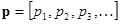Одной из наиболее важных характеристик СМО является значение средней длины очереди.

Для системы M/G/1 она дается формулой Полячека-Хинчина. Определим в пределе длину очереди как .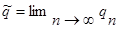

Анализируя два случая ухода требования С_n когда система остается непустой (Рис. 3.2) и случай ухода требования, когда система остается пустой (Рис.3.3),

Получаем два соотношения, связывающие случайные величины, определяющие число требований:

Для непустой .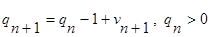

Для пустой .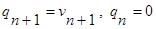

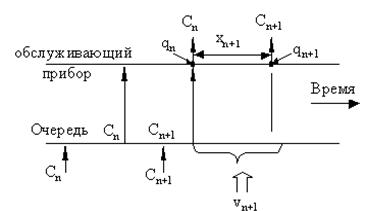
Рис. 3.2 Случай q_n >0.

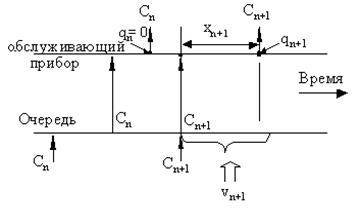
Рис. 3.3 Случай q_n =0.

Если ввести ступенчатую дискретную функцию

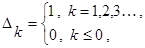
то можно объединить эти соотношения в одно:

.

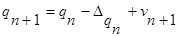Из этого уравнения получим искомое значение средней длины очереди следующим образом. Возведем в квадрат правую и левую часть, а затем определим математическое ожидание от правой и левой части.

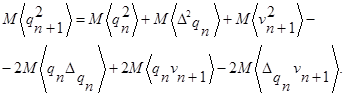
Переходя к пределу при n→∞ , можно получить

.

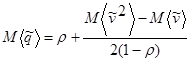Здесь неизвестно только математическое ожидание от квадрата случайной величины, называемое вторым моментом распределения. Мы не будем вдаваться в тонкости вычисления этой величины, что могло бы быть полезно само по себе, и запишем сразу соотношение для числителя

.

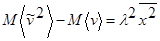Теперь можно выписать окончательный результат для средней длины очереди в момент ухода обслуженного требования, выражающийся через известные величины – коэффициент использования ρ и второй момент распределения времени обслуживания .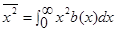

Эта формула и получила название формулы Полячека –Хинчина

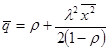
В частном случае формула позволяет найти среднюю длину очереди и для показательного распределения времени обслуживания (система M/M/1) и для детерминированного времени обслуживания (система M/D/1) . В первом случае достаточно подставить значение второго момента для показательного распределения равное 1/λ², а для второго случая положить второй момент равный нулю.

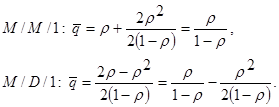
Как видно, уменьшение дисперсии времени обслуживания несколько снижает длину очереди.

Наконец, воспользовавшись формулой Литтла, которая справедлива и в рассматриваемом случае, получим значение среднего времени обслуживания в системе M/G/1.

Обозначим T –среднее время пребывания требования в системе. По формуле Литтла:

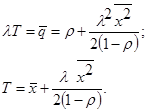
Таким образом, мы определили все важнейшие характеристики системы с произвольным распределением времени обслуживания в сервере.