Система с несколькими серверами: M/M/m

Рассмотрим сначала простой случай системы, содержащей два сервера, любой из которых доступен для поступающих на вход заявок. Системы с несколькими серверами такого типа называют полнодоступными. Очевидно, что по сравнению с односерверной системой производительность будет выше. Сразу отметим, что интерес будет представлять сравнение с односерверной системой интенсивность обслуживания в которой в среднем вдвое выше, то есть мы ответим на вопрос что эффективнее удвоение скорости обработки или распараллеливание обработки.

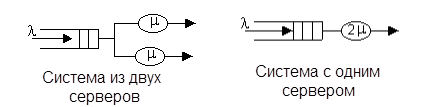
Система M/M/2 может быть представлена как процесс размножения-гибели с параметрами:

Найдем сначала распределение вероятностей в стационарном режиме:

Находя из условий нормировки вероятность простоя (нулевого состояния), находим

Найдем теперь основные характеристики качества обслуживания. Средняя длина очереди составит:

.

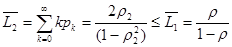Теперь найдем среднее время задержки в системе по формуле Литтла:

.

Таким образом, в системе с двумя серверами время задержки сокращается. Нетрудно убедиться, что производительность системы M/M/2 также выше, поскольку теперь средняя производительность будет определяться вероятностью занятости только одного сервера и незанятости обоих серверов:

.

Получилось, что производительность системы без блокировки также как и для системы с одним сервером совпадает с входной нагрузкой, тогда как максимальная производительность могла равняться 2μ .

Найдем теперь для сравнения характеристики качества обслуживания для односерверной системы с вдвое большей пропускной способностью сервера μ. Воспользуемся формулами для системы M/M/1.

На рис. 1.16 представлены нормированные графики среднего времени задержки в системе с одним и с двумя серверами одной и той же производительности и с одним серверов, работающим с вдвое большей скоростью. Как видно из сравнения, увеличение вдвое скорости работы сервера оказывается более эффективным, чем введение параллельного сервера той же производительности.

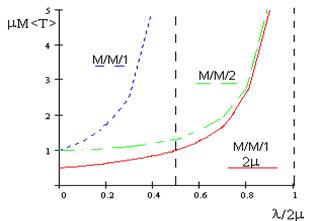
Рис. 1.16 Нормированные графики среднего времени задержки в системе с одним и с двумя серверами одной и той же производительности и с одним серверов, работающим с вдвое большей скоростью.

Рассмотрим теперь общий случай СМО с m серверами. Диаграмма интенсивностей переходов для такой системы представлена на рис. 1.17.

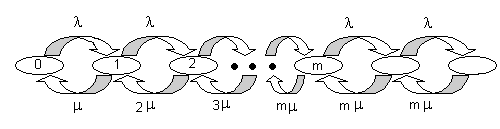
Рисунок 1.17. Диаграмма интенсивностей переходов для СМО типа M/M/m.

Интенсивности переходов могут быть определены следующим образом:

Используя основные общие соотношения для процессов гибели-размножения, получим:

Вероятность простоя определяется громоздкой формулой, которая может быть записана через общую входную нагрузку А и удельную нагрузку r на один сервер:

.

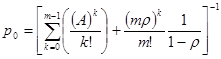Полученные здесь соотношения позволяют рассчитать все характеристики QoS, мы приведем только одну формулу, позволяющую найти вероятность того, что поступающее в систему заявка окажется в очереди. Эту формулу широко используют в телефонии: она определяет вероятность того, что поступающий на пучок из m линий вызов, не застанет ни одной свободной линии и будет поставлен в очередь на обслуживание. Эту формулу часто называют С-формулой Эрланга.

Модель СМО, описываемая С - формулой Эрланга называется также Lost Calls Delayed (LCD).

1.3.4 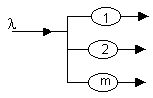Система обслуживания с m серверами и с явными потерями: M/M/m:Loss

Предметом рассмотрения теперь будет система без образования очереди для заявок, поступивших в моменты, когда все m серверов были заняты. Такие заявки будут просто теряться. В телефонии это типичный случай коммутирования на конечном коммутационном поле. Опишем такую систему подходящим процессом типа гибели-размножения. Его параметры могут быть определены так

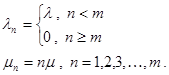
Такая система оказывается также эргодичной и диаграмма интенсивностей переходов, приведенная на рис. 1.18 позволяет найти распределение вероятностей:

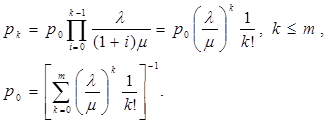
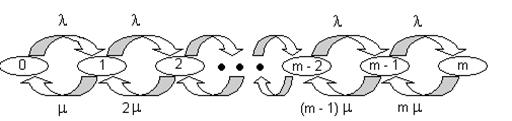
Рис. 1.18 Диаграмма интенсивностей переходов для СМО типа M/M/m:Loss.

Основной характеристикой QoS для этой системы является средняя доля времени, когда все серверы оказываются занятыми. В этом случае говорят о том, что в системе наступила блокировка. Вероятность такой блокировки определяется по формуле, носящей в телефонии название В - формулы Эрланга или формулой потерь Эрланга

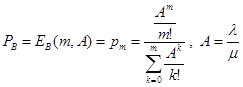
Эта формула играет столь большую роль в телефонии, что ее значения табулированы и существует масса таблиц, обратного расчета, то есть определения нагрузки, при которой обеспечивается заданная вероятность блокировки для заданного числа серверов. Такая таблица важна при расчетах многих сетей и систем массового обслуживания. Модель СМО, описываемая В - формулой Эрланга называется также Lost Calls Cleared (LCC).