Тема 1.1. Дифференциальное и интегральное исчисление.

1.Функции одной независимой переменной.

При изучении различных явлений природы, а также при решении инженерных, технических задач мы замечаем, что одни величины сохраняют одно и тоже численное значение, а другие величины связаны между собой определенной зависимостью.

Все величины делятся на постоянные и переменные.

Величина называется постоянной, если она в условиях данного эксперимента сохраняет одно и тоже значение. Например, длина радиуса одной и той же окружности, температура кипения воды при постоянном давлении.

Величина называется переменной, если она в условиях данного эксперимента может принимать различные значения. Например, зависимость площади круга от его радиуса 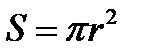, величина заработка рабочего при сдельной оплате труда зависит от фактической выработки и др.Следует заметить, что радиус круга, фактическая выработка рабочего не могут быть отрицательными величинами и каждому значению этих величин соответствует значение площади круга и величина заработка – во втором.

Обобщая эти примеры, можно получить следующие определения.

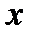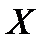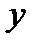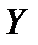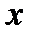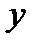Если каждому элементу из множества по некоторому правилу (закону) ставится в соответствие единственный элемент другого множества , то говорят, что между элементами(переменными) и существует функциональная зависимость; при этом переменную величину 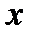называют независимой переменной, или аргументом, а переменную величину 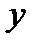- зависимой переменной, или функцией

2. Производной функцией 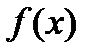в точке 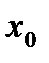называется предел отношения приращения 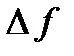функции в этой точке к приращению 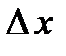аргумента, когда последнее стремится к нулю: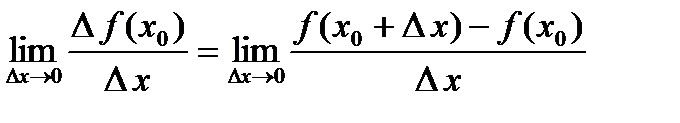

Функция 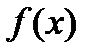, имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой в этом промежутке.

Для производной функции 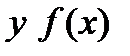употребляются следующие обозначения:

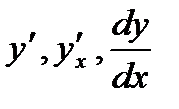или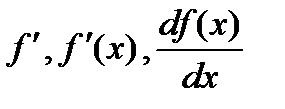

Нахождение производной функции называется дифференцированием.

Вычисление производной функции 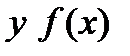производится по правилам дифференцирования.

Если 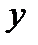есть функция от 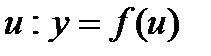, где 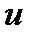, в свою очередь, есть функция от аргумента 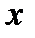, то 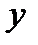называется сложной функцией от 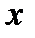(функцией от функции)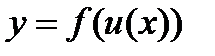

Производная сложной функции равна произведению ее производной по промежуточному аргументу на производную этого аргумента по независимой переменной:

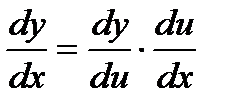или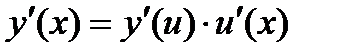

Физический смысл производной

При прямолинейном движении точки скорость 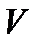в данный момент 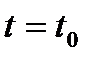есть производная 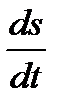от пути 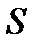по времени 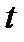, выполненном при 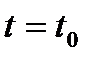, то есть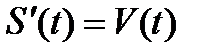

Ускорение в данный момент 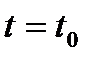есть производная 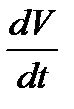от скорости 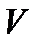по времени 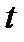, вычисленная при 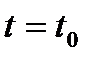, то есть: 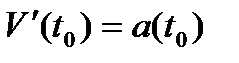или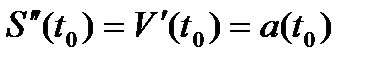

Пусть 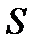выражен в метрах (м), время 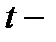в секундах (с), скорость 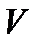в м/с, ускорение 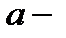в .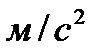

Геометрический смысл производной

Касательная есть предельное положение секущей.

Существование производной функции 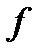в точке 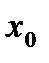равносильно существованию касательной в точке 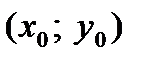графика, при этом угловой коэффициент касательной равен 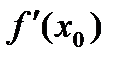то есть: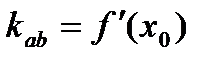

Уравнение прямой с угловым коэффициентом 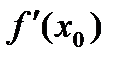имеет вид: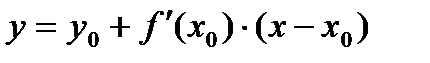

1.Найти производные следующих функций:

а) 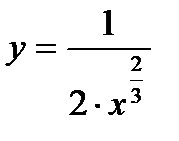; б)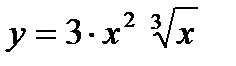

Решение: Преобразуем функции к виду :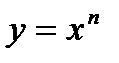

а) ;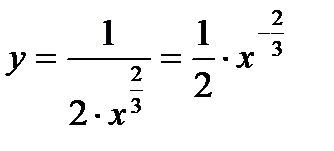

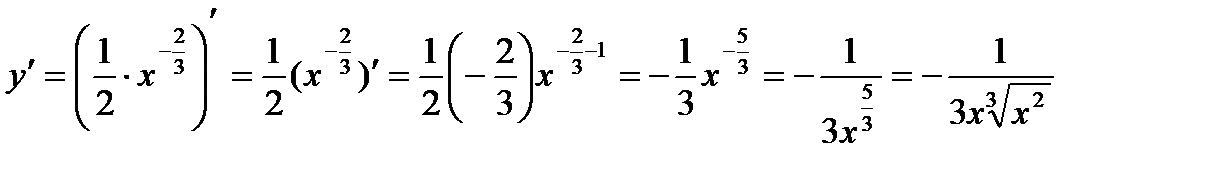
б)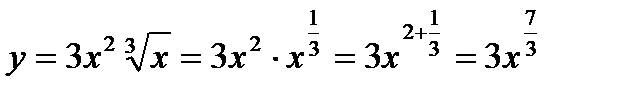

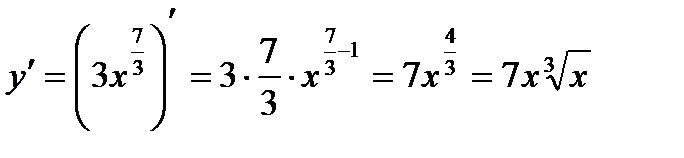
2.Найти производную функции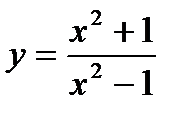

Решение: Используя формулы основных правил дифференцирования, получим:

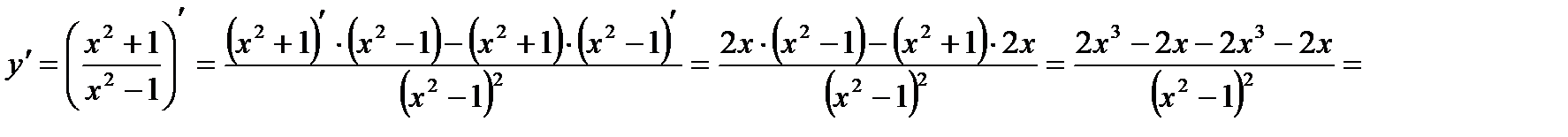
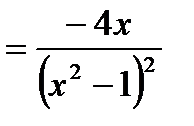
3.Найти производную функции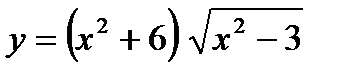

Решение: Используем формулы производной произведения, получим:

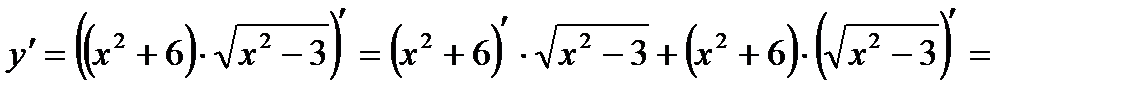
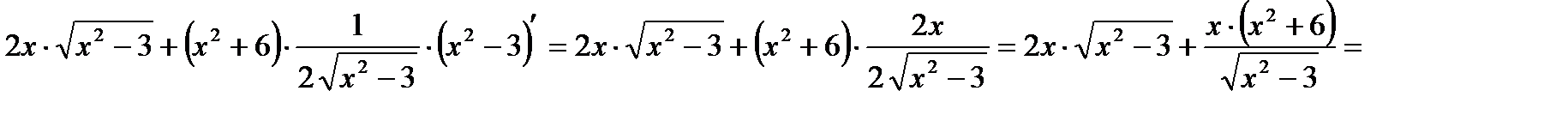
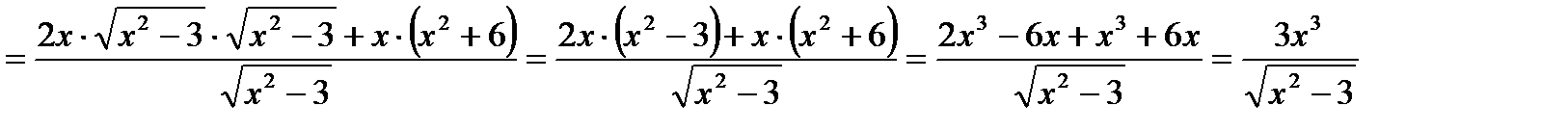
4.Найти производные следующих функций:

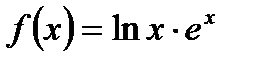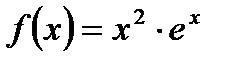а) ; б) ; в) .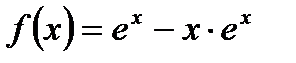

Решение: а) Используя основные правила дифференцирования получим:

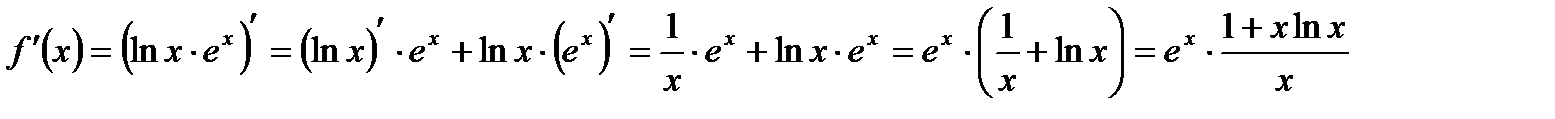
б) Используя формулы дифференцирования получим:

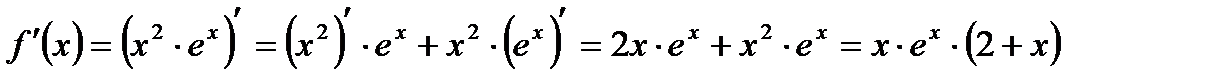
в) Используя формулы и основные правила дифференцирования, получим:

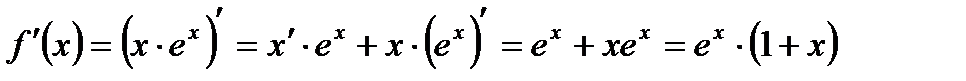
5.Тело массой 10 кг движется прямолинейно по закону 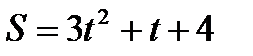. Найти:

а) действующую силу; б) кинетическую энергию тела через 4 с после начала движения.

Решение:

Найдем скорость движения тела:

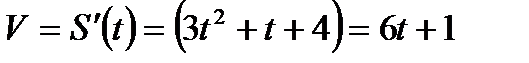
Вычислим скорость в момент времени 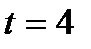с: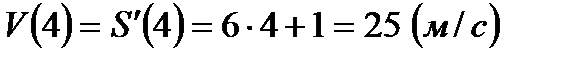

Определим кинетическую энергию: ;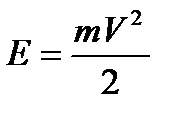

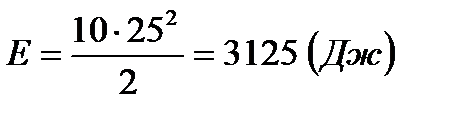
Найдем действующую силу: 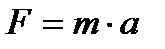Значит, найдем ускорение: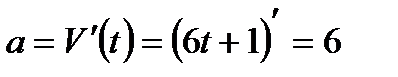

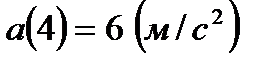
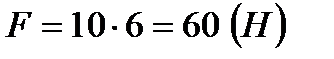
6.Написать уравнение касательной к графику функции 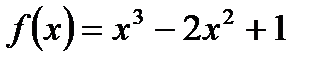в точке .

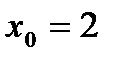Решение:

По условию 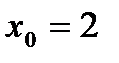, значит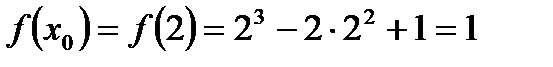

Найдем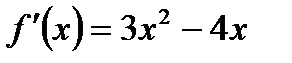

Так как 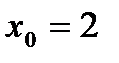, то

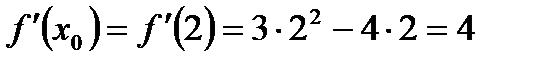
Подставляя эти числа в уравнение касательной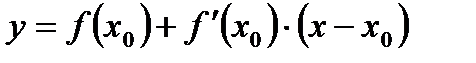

получим 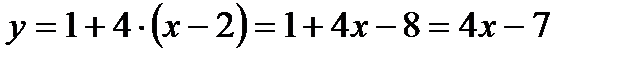Ответ: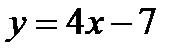

3.С помощью производной можно находить промежутки монотонности функции.

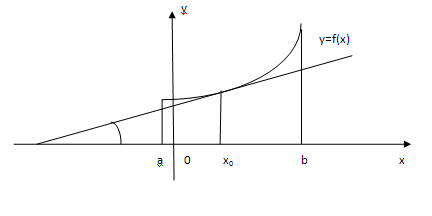
Если функция 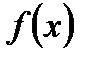имеет на интервале (а; в) положительную производную, то касательная к ее графику в каждой точке направлена вверх, т. е. образует острый угол с положительным направлением оси ОХ. Это означает, что функция 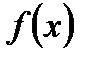возрастает на интервале (а; в).

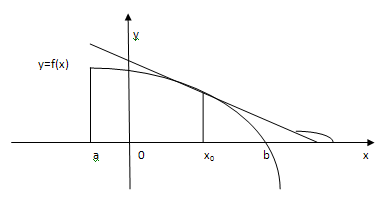
Если производная функции 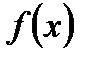отрицательна на интервале (а; в), то касательная к ее графику в каждой точке направлена вниз, т. е. образует тупой угол с положительным направлением оси ОХ. Это означает, что функция 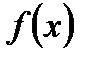убывает на интервале (а; в).

То справедливо утверждение:

Теорема: Пусть функция 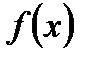дифференцируема на некотором промежутке.

Если 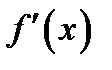> 0 на всем промежутке, то функция 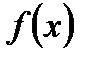возрастает на этом промежутке.

Если 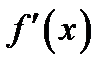< 0 на всем промежутке из некоторой окрестности точки 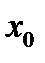выполняется неравенство: .

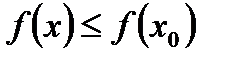- Точка 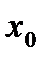называется точкой минимума 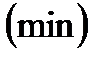функции 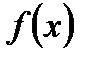, если для всех 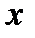, из некоторой окрестности точки 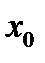выполняется неравенство: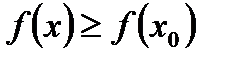

- Точки минимума и максимума называются точками экстремума .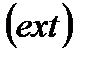

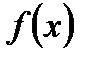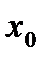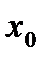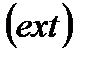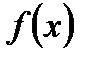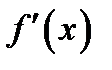Теорема Ферма: Пусть функция определена в некоторой окрестности точки и дифференцируема в этой точке. Если - точка экстремума функции , то =0

Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называется критическими точками этой функции.

Возрастающие и убывающие функции называются монотонными, а промежутки, в которых функциях возрастает или убывает – промежутками монотонности.

Свойства функции определяются по поведению ее производной:

производная положительна – функция возрастает; производная отрицательная – функция убывает. Производная в точке 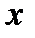обратилась в нуль – значит ничего определенного о ее поведении сказать нельзя и надо посмотреть на изменение знака производной при прохождении через точку 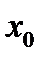. Если производная изменила свой знак с «+» на «-», то в точке 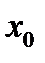- максимум, если знак изменился с «-» на «+», то в этой точке - минимум, если производная свой знак не

изменила, то экстремума в точке 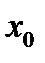нет. Точки, в которых производная обращается в нуль, называются критическими точками функции.

Для построения графика функции исследуют свойства функции с помощью производной.

Общая схема исследования функции:

1. Найти область определения;

2. Выяснить является ли функция четной или нечетной, периодической;

3. Найти точки пересечения графика с осями координат;

4. Найти промежутки знакопостоянства, т. е. решить неравенство 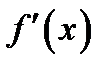> 0 методом интервалов;

5. Исследовать монотонность и найти экстремумы. Вычислить производную, найти ее корни (критические точки), нанести на числовую ось определить знаки производной, определить характер поведения функции;

6. Вычислить значение функции: в критических точках, при 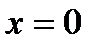на концах области определения. Исследовать поведение функции вблизи «особых точек», например, там, где знаменатель обращается в нуль. Результаты исследования удобно записать в виде таблицы;

7. Используя таблицу построить график функции.

1.Найти промежутки возрастания или убывания.

1.1.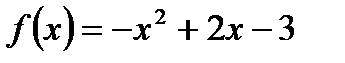

Решение:

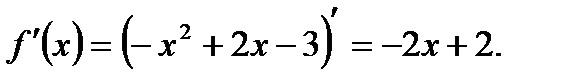
если 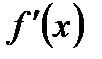> 0, то 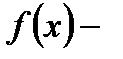возрастает. 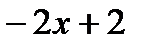> 0; > ; < .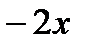

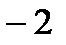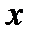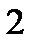на 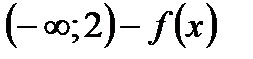возрастает,

если 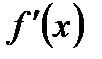< 0, то 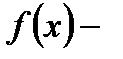убывает. 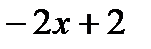< 0; > ; > .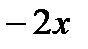

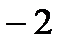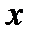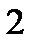на 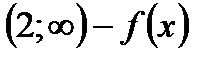убывает.

1.2.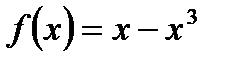

Решение: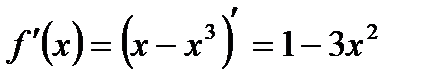

если 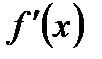> 0, то 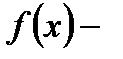возрастает, значит

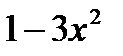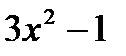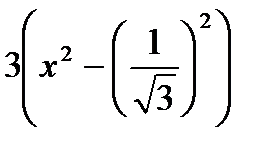> 0; < 0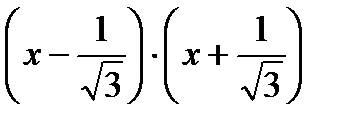; < 0. < 0.

Решим методом интервалов:

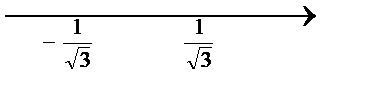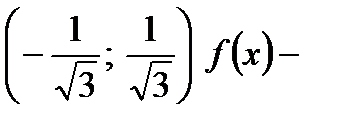на возрастает.

Аналогично, если 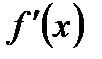< 0, то 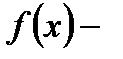убывает. 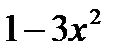< 0, или 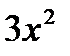> > 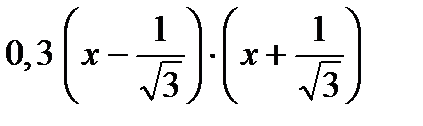0. на 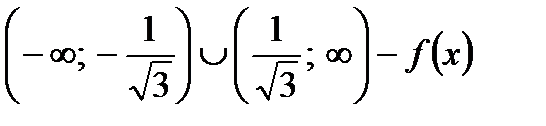убывает.

1.3.Исследовать функцию 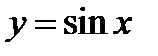и построить график.

Решение:

1) .

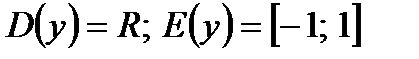2) 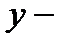нечетная т. к. 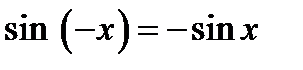; 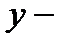периодическая, 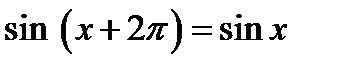. Поэтому проведем исследования на .

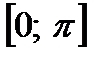3)

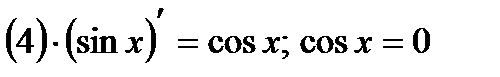
Заполним таблицу

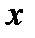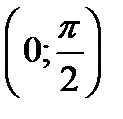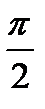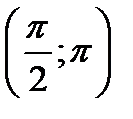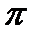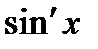		+		-	-1

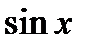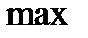Строим график 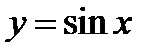на .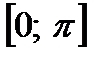

4.Функция 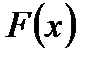называется первообразной для функции 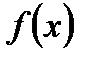в промежутке: 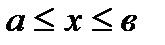, если в любой точке этого промежутка ее производная равна :

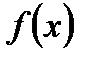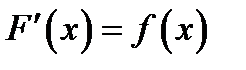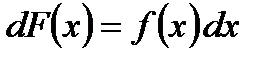, или , на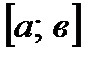

Отыскание первообразной функции по заданной ее производной 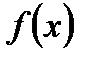или дифференциалу 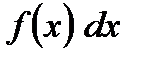есть действие, обратное дифференцированию – интегрирование. Совокупность первообразных для функции 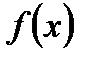или для дифференциала 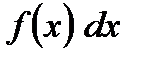называется неопределенным интегралом и обозначается символом 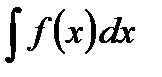. Таким образом: ,

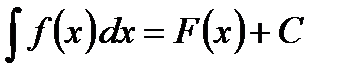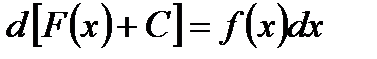
Здесь 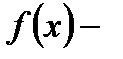подинтегральная функция, 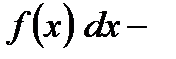подинтегральное выражение, 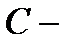произвольная постоянная.

Определенным интегралом от функции 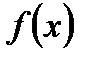на отрезке 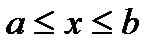называется предел интегральной суммы при условии, что длина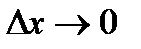

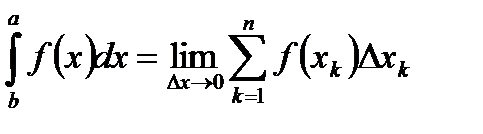
Для вычисления определенного интеграла от функции 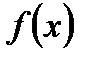в том случае, когда можно найти соответствующий неопределенный интеграл 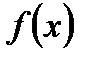служит формула Ньютона-Лейбница: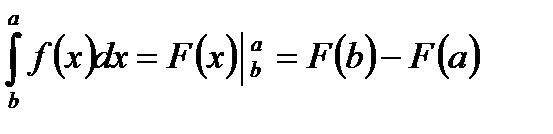

Существуют следующие методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям.

Найти следующие интегралы:

1.

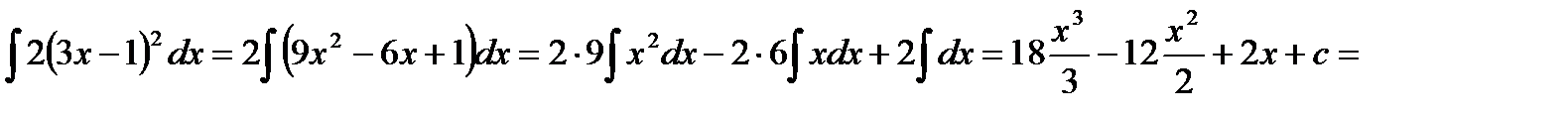
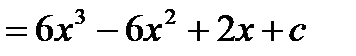
2. 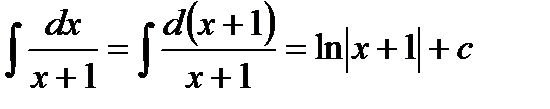, т. к.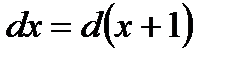

3. 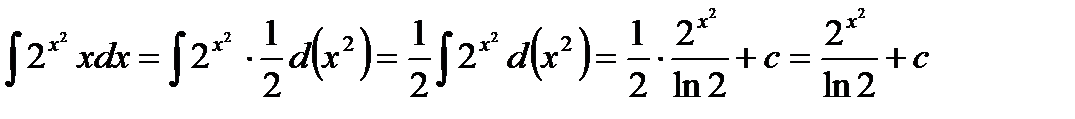, т. к.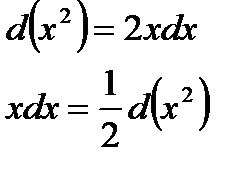

4. ,

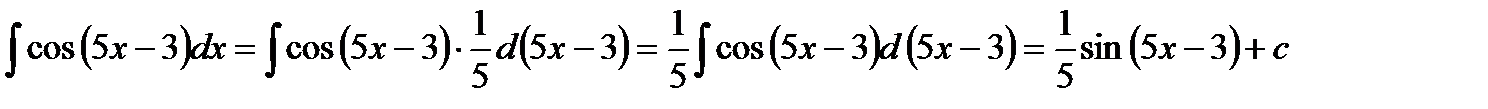т. к.

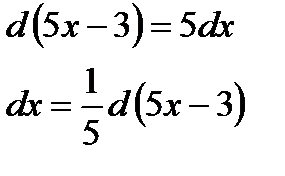
5.

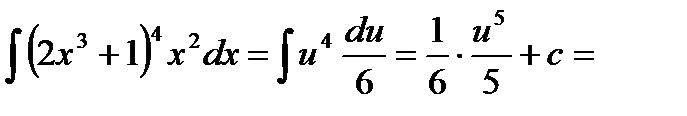
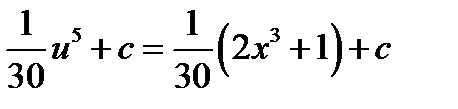
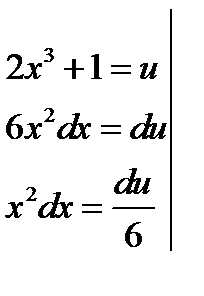
5. Применение интеграла к вычислению различных величин. Определенный интеграл широко применяется при вычислении различных геометрических и физических величин. Вычисление некоторой величины и соответствующий промежутку 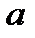< < 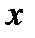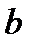изменения независимой переменной 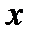, выполняется по следующей схеме: 1) Пусть величина и получит приращение 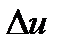~ 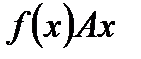, соответствующее изменению 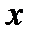на малую величину 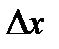; 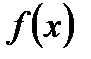рассматривается как данная или определяемая из условия задачи функции от .

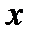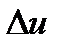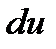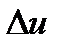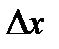2) Заменив приращение дифференциалом (главная часть приращения ) и - дифференциалом 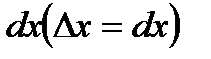, получим .

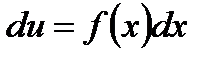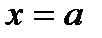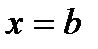3) Интегрирую это равенство в пределах от до , находим .

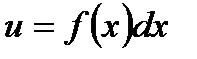2. Вычисление площади плоской фигуры.

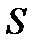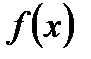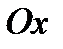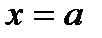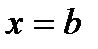Найдем площадь криволинейной трапеции ограниченной кривой , осью и двумя прямыми и , где < < , > .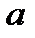

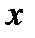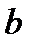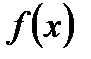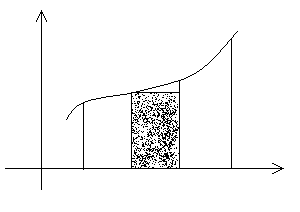
Вычисленные пути, пройденного точкой.

Путь пройденный точкой при неравномерном движении по прямой с переменной скоростью 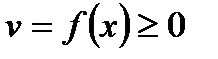за промежуток времени от 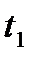до 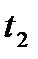вычисляется по формуле: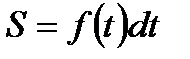

5. Вычисление работы силы.

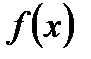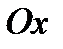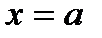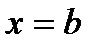Работа произведенная переменной силой при перемещении по оси материальной точки от до находится по формуле: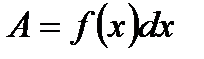

При решении задач на вычисление работы силы часто используется закон Гука: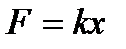

где 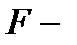сила (Н), 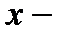абсолютное удлинение пружины (м), 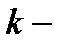коэффициент пропорциональности .

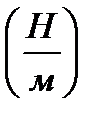1.Вычислить площадь фигур, ограниченных указанными линиями:

1.1.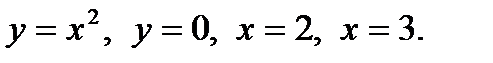

Решение: Построение.

Графиком 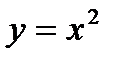является парабола.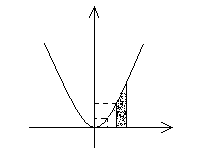

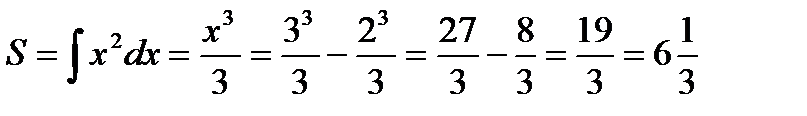(кв. ед.)

1.2.Скорость движения точки изменяется по закону 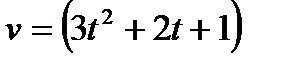м/с. Найти путь пройденный точкой за 10 с. от начала движения:

Решение: По формуле находи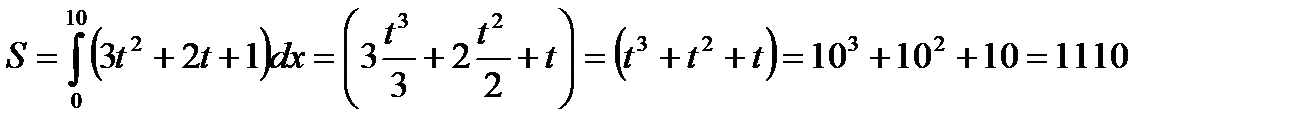м:

(м)

1.3.Сжатие 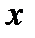винтовой пружины пропорционально положительной силе 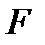. Вычислить работу силы 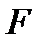при сжатии пружины на 0,04 м, если для сжатия ее на 0,01 м при 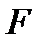= 10 Н, то подставляя эти значения в формулу (8), получим:

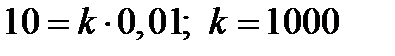Н/м

Подставив в (8) значение 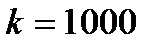Н/м получим 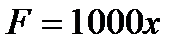т. е. 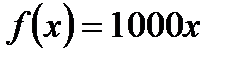. Искомую работу найдем по формуле:

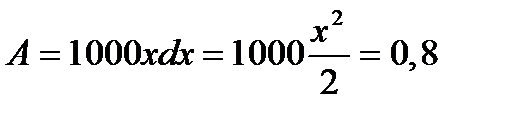(Дж)

Вопросы для самопроверки:

1. Дать определение производной функции 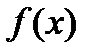в точке .

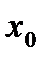2. Какая функция называется дифференцируемой?

3. Какие обозначения употребляются для производной?

4. Как называется нахождение производной?

5. Перечислить основные правила дифференцирования.

6. Какая функция называется сложной?

7. Как вычислить производную сложной функции?

8. В чем заключается физический смысл производной?

9. В чем заключается геометрический смысл производной?

10. Чему равен угловой коэффициент касательной?

11. Сформулируйте признак возрастания функции.

12. Сформулируйте признак убывания функции.

13. Какая точка называется точкой максимума?

14. Какая точка называется точкой минимума?

15.Какие точки называются точками экстремума?

16. Какие точки называются критическими?

17. Дайте определение первообразной функции.

18. Какое действие называется интегрированием?

19. Что называется неопределенным интегралом?

20. Каким символом обозначается интеграл?

21. Напишите таблицу основных интегралов.

22. Сформулируйте основные свойства интегралов.

23. Какую фигуру называют криволинейной трапецией?

24. Что называют определенным интегралом?

25. Сформулируйте формулу Ньютона-Лейбница.

26. Какие методы интегрирования существуют?

27. Какую фигуру называют криволинейной трапецией?

28. Сформулируйте формулу Ньютона-Лейбница.