Особый класс задач с неделимостями составляют целочисленные ТЗ, в которых целочисленные решения обеспечиваются при целочисленности исходных данных.

Переход от задач с дискретными переменными к целочисленным задачам

1. Изменение масштаба.

2. Преобразование системы ограничений:

а) пусть

Введем бинарную переменную y_ij, принимающую значения 0, 1.

, при условиях

.

То есть мы перешли от произвольных дискретных переменных к бинарным.

б) аналогично можно преобразовать задачу целочисленного программирования в задачу с бинарными переменными, если .

Поэтому в дальнейшем будем рассматривать задачи с целочисленными переменными.

- задачи с альтернативными переменными (или с логическими условиями). В этих задачах вводятся искусственные альтернативные переменные, отражающие логические условия задачи. Это задачи с дополнительными логическими условиями (“или-или”, “если, то”).

Наиболее распространенными являются задачи целочисленного программирования, так как любую дискретную задачу можно привести к целочисленной.

Прикладные дискретные модели

Задача о раскрое.

Для изготовления заготовок D₁,…,D_m имеется n способов раскроя материала A₁,…,A_n. -количество заготовок i-го типа, получаемых из единицы материала при способе A_j. Имеется D единиц материала. При раскрое единицы материала по способу A_j имеются отходы площадью . Надо произвести не менее заготовок i-го типа и выполнить план с минимизацией отходов.

Таблица 11

Виды заготовок	Способы раскроя	План производства
A1	A2	…	An
D1 D2 … Dm	A11 a21 ... am1	a12 a22 ... am2	... ... ... ...	a1n a2 n ... amn	b1 b2 ... bm
Отходы	C1	c2	…	cn

Пусть - количество единиц материала, раскраиваемого по j-му способу.

Математическая модель задачи запишется следующим образом:

;

.

Задача о ранце. Имеются предметы n видов, для каждого предмета j-го вида (j=1,n) известны его объем и стоимость . Необходимо определить такой набор предметов, суммарный объем которых не превышал бы заданного числа b, а суммарная ценность была бы максимальной. Эта задача интерпретируется как задача загрузки ранца объема b и называется одномерной задачей о ранце.

Введем целочисленные переменные , значения которых характеризует количество предметов j-го вида, помещенных в ранец. Тогда математическая модель данной задачи имеет вид:

Если ограничениями могут быть не только объем ранца, но и другие его характеристики , то получим многомерную задачу о ранце.

В случае, если количество предметов j-го вида ограничено и равно , к задаче добавляется ограничение . Если =1, то получим задачу о ранце с булевыми переменными. Тогда , причем , если j-й предмет помещен в ранец, в противном случае.

К задаче о ранце сводится широкий класс задач дискретной оптимизации с ограниченными ресурсами.

Пример. Для оценки работоспособности систем перед их эксплуатацией производится проверка их функционирования. При проверке контролируются отдельные параметры системы, каждый из которых характеризуется вероятностью отказа проверяемых элементов и временем контроля . Так как допустимое время контроля всей системы T ограничено, то для проверки необходимо выбрать параметры, контролирующие наиболее ненадежные элементы и требующие для контроля наименьшего времени.

Пусть n – общее количество параметров. Введем альтернативные булевы переменные:

Тогда математическую модель задачи можно сформулировать как одномерную задачу о ранце:

Задача о назначениях.

Линейная задача о назначениях .

Имеется n исполнителей и n видов работ, которые они могут выполнять. Пусть 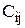- производительность i-го исполнителя при выполнении j работы. Каждый исполнитель может выполнять один вид работ, а каждый вид работ может быть выполнен одним исполнителем. Требуется таким образом распределить исполнителей по видам работ, чтобы общая производительность была максимальной.

Введем альтернативные переменные :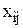

Тогда математическая модель задачи имеет вид:

Иногда задача о назначениях формулируется как задача минимизации, если в качестве выбирается время, затраченное i-м исполнителем на выполнение j-й работы.

Необходимо заметить, что условие целочисленности переменных в задаче о назначениях можно не накладывать, т.к. эта задача является частным случаем транспортной задачи и при целочисленности правых частей ограничений целочисленность решения обеспечивается автоматически.

К задаче о назначениях сводится широкий круг задач дискретной оптимизации (распределение исполнителей по видам работ, закрепление за станками операций, распределение задач между различными ЭВМ, назначение претендентов на вакантные должности при формировании штатного расписания и т.д).

Пример . При передаче сообщений по каналу с шумом необходимо каждой букве передаваемого алфавита поставить в соответствие букву принимаемого таким образом, чтобы сумма вероятностей правильности принимаемых букв была бы максимальна.

Пусть - вероятность соответствия принимаемой j-й буквы передаваемой i-й букве. Введем альтернативные переменные:

Тогда математическая модель задачи будет иметь следующий вид:

Квадратичная задача о назначениях.

Имеется m пунктов, в которых необходимо разместить n объектов. В каждом пункте может быть размещен только один объект. Даны расстояния между i-м и j-м пунктами , а также c_sk – показатели, характеризующие взаимосвязи между s-м и k-м объектами (стоимость перевозок, число коммукникаций и т.д.). Необходимо определить такое назначение объектов в выделенные пункты, чтобы минимизировать соответствующие затраты.

Математическая модель задачи имеет следующий вид:

В данном случае целевая функция зависит не от всевозможных назначений, а от всевозможных пар назначений (s-й элемент размещается в i-й пункт, а k-й – в j-й пункт). Целевая функция при этом не является линейной.

Квадратичная задача о назначениях имеет широкий круг практических приложений. Она может быть использована для решения задач размещения (оборудования, предприятий, деталей, и т.д.). Особенно часто эта модель используется в задачах конструкторско-топологического проектирования.

Пример. Необходимо таким образом разместить n компонентов печатной платы на m позициях монтажного пространства, чтобы суммарная длина электрических соединений между компонентами была бы минимальной.

Предположим, что n=m. Пусть - расстояние между k-й и s-й позициями, - число связей между i-м и j-м компонентами. Введем бинарные переменные

.

Задача коммивояжера

Имеются n пунктов или городов с заданными расстояниями между i-м и j-м пунктами. Необходимо составить оптимальный маршрут из условия минимизации суммарного расстояния для коммивояжера, выходящего из пункта с номером 1, который должен побывать во всех пунктах ровно по одному разу и вернуться в исходный пункт.

Введем альтернативные бинарные переменные :

.

Условия минимизации общего расстояния , а также прибытия в каждый пункт и выезда из него ровно по одному разу могут быть выражены следующим образом:

.

Однако необходимо обеспечить непрерывность маршрута, чтобы набор звеньев, входящих в маршрут, образовывал единую цепочку (например, при n=8 цепочка (1,2) - (2,6) - (6,4) - (4,8) - (8,5) - (5,3) - (3,7) - (7,1)), а не состоял бы из отдельных не связанных цепочек (например, (1,2) - (2,6) - (6,1) и (3,8) - (8,7) - (7,5) - (5,4) - (4,3)). Для устранения замкнутых циклов (подобходов), включающих количество вершин меньшее n, в модель вводятся n дополнительные переменных u_i³0 ( ) и n² дополнительных ограничений:

_.

Действительно, пусть маршрут включает несколько цепочек. Тогда существует цепочка, начинающаяся и заканчивающаяся в начальном пункте, но включающая n₁ звеньев, где n₁<n. Просуммировав эти неравенства вдоль такой цепочки (т.е. при x_ik=1), получим бессмысленное неравенство n₁(n-1)£n₁(n-2) (все u_i и u_j при суммировании взаимно уничтожаются). Покажем теперь, что для маршрута, исключающего подобходы, это неравенство выполняется, т.е., можно найти значения u_i, удовлетворяющие дополнительным ограничениям. Положим u_i=p, если город i посещается коммивояжером на p-м шаге, p= . Отсюда следует, что . Таким образом, ограничения выполняются для всех . При эти ограничения превращаются в равенства

_.

Задача коммивояжера имеет широкий круг практических приложений. К ней сводятся задачи оптимальной маршрутизации (выбор маршрутов перевозки грузов, маршрутов движения транспорта, минимизация расстояния, проходимого исполнительным механизмом станка с ЧПУ и т.д.), задачи проектирования электрических и вычислительных сетей, задачи определения последовательности обработки деталей на станках с условием минимизации времени переналадок и т.д.

Пример 11. Пусть необходимо проложить коммуникации между n различными ЭВМ таким образом, чтобы каждая ЭВМ была связана с двумя соседними, вся сеть была бы подключена к центральной ЭВМ, а суммарная длина коммуникаций была бы минимальна. . Заданы расстояния d_ij между i-й и j-й ЭВМ.

Данная задача формализуется в виде задачи коммивояжера следующим образом:

;

.

При этом x_ij=1, если i-я и j-я ЭВМ соединяются.

Задача о покрытии

Пусть имеется n предметов, каждый из которых обладает некоторым числом признаков из заданного множества m признаков, а в совокупности эти n предметов обладают всеми m признаками. Необходимо выбрать минимальное число предметов, которые в совокупности обладали бы m признаками. Условия задачи задаются матрицей A с элементами

Введем бинарные переменные:

.

Тогда математическая модель задачи имеет следующий вид:

Каждое i-е ограничение в данном случае показывает, что должен быть выбран хотя бы один предмет, обладающий i-м признаком.

Если каждому j-му предмету приписывается вес , может быть сформулирована взвешенная задача о покрытии:

Если каждому i-му признаку приписывается натуральное число и требуется найти минимальное число таких предметов, что i-м признаком обладает не менее предметов из указанного набора, получаем задачу о кратном покрытии:

Задача о разбиении. Задача о разбиении аналогична задачи о покрытии с тем отличием, что признаки у различных предметов не должны совпадать:

Задача о взвешенном разбиении формулируется следующим образом:

К задаче о покрытии сводится широкий круг задач информационного поиска, синтеза логических схем, задачи разбиения электронных схем на модули и покрытия схем типовыми ячейками и т.д.

Пример. Пусть некоторое количество информации хранится в n массивах (файлах) длины , причем на каждую единицу информации отводится по крайней мере один массив. Задана матрица T с элементами

Получена заявка на m типов единиц информации. Необходимо определить подмножество массивов минимальной длины, необходимых для удовлетворения заявки.

Введем бинарные переменные:

.

Тогда математическая модель задачи формализуется в виде задачи о покрытии: