Типы распределительных задач

1. Простые распределительные задачи:

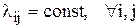
2. Задачи с однородными ресурсами и разнородными потребностями:

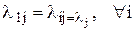(столбцы матрицы с элементами l_ij одинаковы)

3. Задачи с разнородными взаимозаменяемыми ресурсами и однородными потребностями:

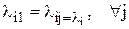(строки матрицы 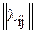одинаковы)

4. Задачи с пропорциональными ресурсами:

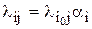, где 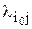– элементы строки матрицы 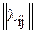, принятой за единичную.

Ресурсы и потребности неоднородны (строки матрицы 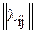, элементы которой устанавливают связь между единицами ресурсов и потребностей, пропорциональны). Числа 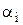называют индексами i-тых ресурсов.

5. Распределительные задачи общего вида.

Приведение к ТЗ

2.

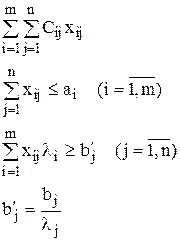
3.

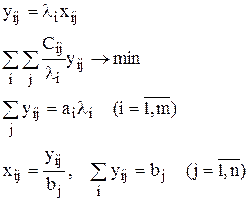
4. .

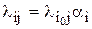Подставим в модель:

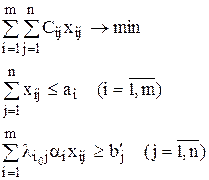
Обозначим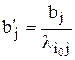

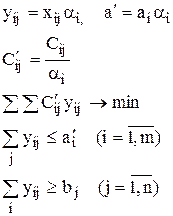
5. В этом случае распределительная задача не можетбыть приведена к транспортной. Для ее решения может быть использованы методы, предназначенные для решения распределительных задач (например, обобщенный метод потенциалов).

Таким образом задача о назначениях – частный случай ТЗ, а распределительная задача – ее обобщение.

Пример

К распределительным задачам сводятся задачи размещения заказов и загрузки оборудования.

А) Пусть имеется m видов оборудования с ресурсами а₁ … а_m станко/ч, и n видов выпускаемых изделий с плановыми заданиями на выпуск b₁ … b_n. l_ij – производительность i-того оборудования при изготовлении j-го изделия (руб/ч).

Модель:

(ограничения по ресурсам)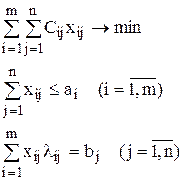

Здесь x_ij – время, затрачиваемое оборудованием i-того вида на изготовление изделия j-го вида.

Б) Если обозначить через x_ij количество изделий j-го вида, изготавливаемых на i-том оборудовании, то задача примет вид:

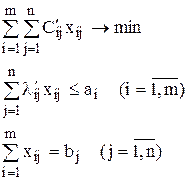
где 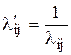– затраты времени i-того оборудования на изготовление единицы изделия j-го вида (или в общем виде количество единицы i-того ресурса, необходимых для удовлетворения единицы j-х потребностей).

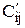– себестоимость единицы j-го изделия при изготовлении на i-м оборудовании (руб/шт).

Задачи дискретной оптимизации

Задачи дискретной оптимизации – это задачи оптимизации, в которых на варьируемые параметры накладывается требование дискретности.

Постановка задачи

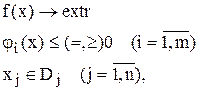
где D_j– множество допустимых значений каждой переменной. При этом предполагается, что хотя бы одна переменная x_j может принимать дискретные значения.

Классификация задач ДП

1. В зависимости от характера ЦФ задачи ДП делятся на линейные и нелинейные. Наиболее изученным в настоящее время является класс линейных задач ДП.

2. В зависимости от характера изменения варьируемых параметров различают задачи

- полностью дискретные

- частично дискретные (или дискретно-непрерывные)

- целочисленные задачи (в которых переменные принимают целочисленные значения)

- задачи с булевыми переменными (переменные могут принимать значения 0, 1). Если ЦФ принимает действительные значения, то задачи оптимизации с булевыми переменными называют задачами псевдобулевой оптимизации.

3. В зависимости от характера (конечности) множества допустимых решений

- комбинаторные задачи (задачи, множество допустимых решений которых конечно)

4. В зависимости от физического смысла варьируемых параметров

- задачи с неделимостями, в которых переменные представляют собой физические неделимые величины(единицы продукции различных видов). К ним относятся все рассмотренные выше ЗЛП, в которых на переменные дополнительно наложены условия целочисленности (распределение ресурсов, планирование и т.д.).