В теории двойственности важное значение имеют две теоремы, определяющие связь между решениями прямой и двойственной задач.

Теорема двойственности. Если из пары двойственных задач одна имеет оптимальный план, то и вторая тоже имеет оптимальный план, причем оптимальные значения целевых функций обеих задач равны между собой:

.

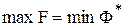При этом 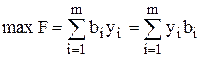. Отсюда следует, что двойственная переменная y_i является коэффициентом при b_i и, следовательно, показывает, как изменится целевая функция при изменении i- го ресурса на единицу. В литературе двойственные переменные часто называют двойственными оценками.

Теорема равновесия. План 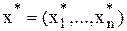прямой задачи и план 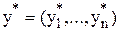соответствующей двойственной задачи являются оптимальными при выполнении следующих условий:

- если при подстановке компонент оптимального плана 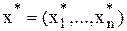в систему ограничений исходной задачи i-е ограничение обращается в неравенство, то i-я компонента оптимального плана двойственной задачи 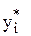равна нулю.

- если i-я компонента оптимального плана двойственной задачи 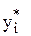положительна, то i-е ограничение исходной задачи удовлетворяется ее оптимальным решением как строгое равенство.

Таким образом, в парах соотношений

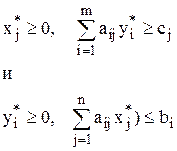
из знака строгого неравенства во одном соотношении каждой пары следует знак строгого равенства в другом.

Условия теоремы равновесия часто записывают в виде

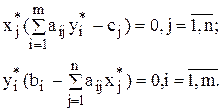
и называют условиями дополняющей нежесткости.

Из рассмотренных теорем можно сделать следующие выводы:

А) Всякий раз, когда i-е ограничение прямой задачи обращается в строгое неравенство, i-я компонента решения двойственной задачи обращается в 0.

Аналогично, всякий раз, когда i-е ограничение двойственной задачи выполняется как строгое неравенство, j-ая компонента оптимального плана обращается в ноль.

Б) Обратно, если i-я компонента оптимального плана двойственной задачи положительна, i-е ограничение исходной задачи выполняется как строгое равенство. Верно и для двойственной задачи.

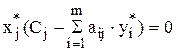
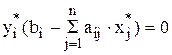
Отсюда следует:

а) Если двойственная оценка y_i^* = 0, то сырье i-го вида не полностью используется при производстве продукции.

б) Если j-е ограничение двойственной задачи выполняется как строгое неравенство, то j-ый вид продукции выпускать экономически нецелесообразно, х_j =0 (т.е. в двойственной задаче цена всех ресурсов больше прибыли)

в) Если y_i ¹ 0, то сырье i-го типа полностью используется при производстве.

Значения двойственных оценок можно определить по симплексной таблице решения прямой задачи следующим образом: -( 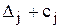), где j-номера столбцов единичных векторов из исходной симплекс-таблицы (на начальной итерации); 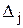-окончательные оценки из последней симплекс-таблицы, соответствующие этим векторам. При этом индексы двойственных оценок определяются номером ограничения, которому они соответствуют.

Необходимо заметить, что если в качестве канонической формы рассматривается задача максимизации, то сумма 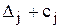берется без знака “-“.

Двойственный симплекс-метод

Пусть необходимо решить задачу линейного программирования, записанную в канонической форме

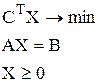
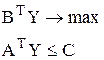
Рассмотрим начальную симплекс-таблицу этой задачи. Очевидно, что в ее столбцах записана прямая задача, а в строках — двойственная. Оценками плана исходной задачи является — с_j, а оценками плана двойственной задачи b_i.

Решим двойственную задачу по симплекс-таблице исходной задачи. Найдем решение двойственной задачи, а вместе с ним опорный план исходной задачи. Этот метод называется двойственным симплекс-методом.

Особенностью двойственного симплекс-метода является то, что его можно применять при решении задач линейного программирования. правые части ограничений которых являются отрицательными числами.

Алгоритм двойственного симплекс-метода.

1. 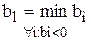(выбор ведущей строки l)

2. Если в ведущей строке l 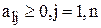, то исходная задача не имеет решения. Если есть 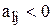, то выбирается ведущий столбец.

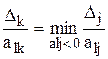- если исходная задача на максимум, то ‘-‘.

3. Пересчет элементов c-таблицы осуществляется по правилу симплекс метода.

4. 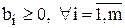- признак оптимальности решения(когда все правые части неотрицательны)