Обобщенная электрическая машина (ОЭМ)

Уравнениям (96), (97)), (103) и (104) соответствует электрическая машина с одной парой полюсов и двумя обмотками на статоре и роторе, расположенными на взаимно-перпендикулярных осях и неподвижными друг относительно друга. Такая электрическая машина называется обобщенной (ОЭМ).

Обобщенная электрическая машина (ОЭМ) характеризуется следующими свойствами:

1. ОЭМ симметрична и имеет равномерный воздушный зазор;

2. магнитопровод машины (ОЭМ) ненасыщен;

3. МДС обмоток имеет синусоидальное распределение по рабочему зазору.

Рис. 13. Модель обобщенной электрической машины (ОЭМ) при записи уравнения для статора в системе координат « 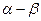» и уравнения для ротора в системе координат « »

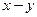Рис. 14. Модель обобщенной электрической машины (ОЭМ) при записи уравнения для статора и ротора в системе координат « »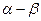

Модель обобщенной электрической машины (ОЭМ) универсальна и при принятии определенных условий, из нее можно получить все типы электрических машин как частные случаи. Например, при питании обмоток статора от двух источников переменного синусоидального тока, смещенных по фазе на 90° , в рабочем зазоре создается круговое вращающееся магнитное поле.

Если одну из обмоток ротора подключить к источнику постоянного тока, то мы получим модель синхронной машины.

Если обе обмотки ротора замкнуть накоротко, то образуется модель асинхронной короткозамкнутой машины.

Если одну из обмоток статора подключить к источнику постоянного тока, а обмотки ротора подключить к двум источникам переменного синусоидального тока с частотой, равной частоте вращения ротора, и фазовым смещением в 90°, таким образом, чтобы поле ротора вращалось в направлении противоположном направлению вращения его вала, то мы получим модель машины постоянного тока. В этой модели поле ротора формируется источниками питания переменного тока с управляемой частотой, роль которых в реальной машине играет источник постоянного тока и коллектор.

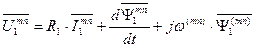. (105)

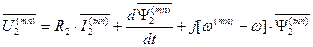. (106)

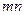Эти уравнения соответствуют модели обобщенной электрической машины в системе координат, вращающейся с произвольной угловой частой . Уравнения, записанные в системе координат « », вращающейся с произвольной угловой частой , можно разложить на составляющие, представив векторные величины в виде комплексных чисел.

. (107)

. (108)

. (109)

. (110)

Из уравнений (107) - (110) следует, что в произвольно вращающейся системе координат ЭДС вращения существует как в статоре, так и в роторе. Наличие ЭДС вращения приводит к появлению перекрестных связей в структуре модели машины, т.к. это слагаемое образуется проекцией потокосцепления на другую ось координат, что существенно затрудняет построение систем управления.

Исключить ЭДС вращения можно надлежащим выбором угловой частоты вращения системы координат, но только либо в уравнениях статора ( 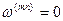), либо в уравнениях ротора ( ).

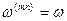Эти уравнения можно представить электрической схемой замещения на рис. 15.

Рис. 15. Электрическая схема замещения по уравнениям АД в произвольно вращающейся системе координат

В короткозамкнутом АД ( ) эти уравнения принимают вид

. (111)

. (112)

При этом отсутствие внешнего источника электрической энергии, питающего ротор короткозамкнутого АД, определяет следующее соотношение частот статора и ротора .

Электромагнитный момент АД

Основной конечной величиной характеризующей электромеханическое преобразование энергии является электромагнитный момент на валу. Он образуется в результате взаимодействия магнитного поля и тока, протекающего в обмотках статора или ротора, и может быть представлен как векторное произведение.

, (113)

где – 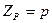число пар полюсов машины.

Можно также представить его в другом виде.

. (114)

В выражениях для электромагнитного момент на валу физический смысл имеет только модуль вектора электромагнитного момента и его можно определить через проекции векторов сомножителей. Для произвольных векторов « 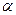» и « » модуль векторного произведения равен разности скалярных произведений проекций векторов на ортогональные оси координат, т.е. – . (115)

; .

. (116)

Учтем выражение (116) и поэтому любое из выражений для электромагнитного момент на валу позволяет найти модуль электромагнитного момента |М|=М, выразив входящие в него векторы через их проекции на координатные оси « 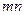». Например, электромагнитный момент определяется через произведение потокосцепления ротора на ток ротора в виде

.

. (117)

Выбор уравнения для расчета электромагнитного момента АД играет большую роль, т.к. некоторые величины АД (в особенности у АД с к.з. ротором) не могут быть измерены. Кроме этого, выбор уравнения для расчета электромагнитного момента АД существенно влияет на сложность математической модели АД, увеличивая порядок системы уравнений модели.

Подготовка уравнений модели короткозамкнутого АД при частотном управлении

Асинхронный привод с частотным управлением является в настоящее время наиболее распространенным. Однако его динамика чаще всего исследуется с помощью упрощенных моделей с отклонениями в малом. Векторная модель АД позволяет получить точную структурную схему, которую затем можно исследовать современными средствами компьютерного моделирования. Рассмотрим на этом примере методику получения передаточных функций сложных объектов с помощью векторных уравнений ОЭМ. Пусть система координат модели АД ориентирована по вектору напряжения статора с частотой питания , т.е. вращается с угловой скоростью, равной 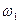. Тогда угловая частота вращения системы координат модели АД в уравнениях (118) и (119) будет определяться частотой сети , т.е. .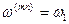

Система координат « 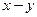», вращающаяся синхронно с потокосцеплением ротора ( 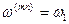при одной паре полюсов) и ориентированная по его направлению, наиболее пригодна для описания процессов в АД.

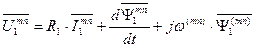. (118)

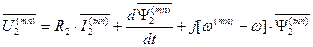. (119)

Из выражений с учетом того, что , а следовательно получим для системы координат « 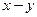», вращающейся синхронно с потокосцеплением ротора ( 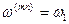) и ориентированной по его направлению.

. (120)

. (121)

Представим обобщенные вектора тока, напряжения и потокосцепления в уравнениях (120) и (121) комплексными векторами, записанными в алгебраической форме в системе координат « ».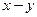

. (122)

. (123)

Раскрывая скобки, преобразуя алгебраические выражения и приравнивая действительные и мнимые части в правой и левой частях выражений (122) и (123) получим четыре уравнения для цепей статора и ротора.

. (124)

. (125)

. (126)

. (127)

Для вычисления модуля электромагнитного момента АД « 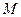» используются векторы потокосцепления статора 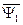и тока ротора .

Подставим в выражение для электромагнитного момента АД выражение для тока статора .

Выражение для тока статора получено из выражения:

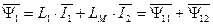. (128)

, (129)

где . (129а)

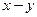Для записи уравнений модели АД применим обобщенные векторы и в системе координат « ». Сначала рассмотрим уравнение для статора.

. (130)

Подставим выражение (129) в уравнение (130) и применим операторную форму записи, заменив символы на символы . Получим

.

После преобразования получим в операторной форме уравнение для статора.

. (131)

, (132)

– электромагнитная постоянная времени статора.

Получив уравнение для статора (132), рассмотрим уравнение для ротора.

. (133)

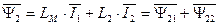. (134)

Преобразуем выражение (133) и применим операторную форму записи, заменив символы на символы . После преобразования получим

. (135)

Преобразуем выражение (134). После преобразования получим

. (136)

Подставим в уравнение (135) 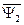из выражения (136). Получим

. (137)

Преобразуем выражение (137). После преобразования получим

. (138)

Разделим правую и левую части выражения (138) на . После преобразования получим в операторную форме уравнение для ротора.

, (139)

где ; (140)

- коэффициент рассеяния.

. (141)

В результате проведенных преобразований вместо четырех уравнений с четырьмя неизвестными обобщенными векторами получили два уравнения (139) и (141) с двумя неизвестным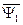и и , с помощью которых можно вычислить модуль электромагнитного момента АД « ».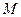

. (142)

Вычитая из уравнения (141) уравнение (139), можно понизить порядок системы уравнений модели АД. В результате проведенных преобразований получим

, (143)

где - расчетный параметр;

- расчетная постоянная времени.

Подготовка уравнений для построения модели АД с кз ротором при частотном управлении в форме структурной схемы

Представим комплексные векторы в выражении (143) в алгебраической форме (в виде вещественных и мнимых составляющих) и определим проекции тока ротора на вещественную и мнимую оси системы координат « 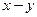», вращающейся с угловой скоростью, равной .

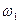. (144)

Определим и , используя уравнения фазовых преобразований (62)-(65).

. (145)

. (146)

Допустим, что . (147)

. (148)

. (149)

Подставим выражения (147)-(149) в уравнения (145) и (146). Получим

. (150)

. (151)

Если проекции обобщенного вектора в неподвижной системе координат « 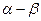» изменяются во времени по синусоидальному закону с частотой 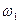, то проекции этого же обобщенного вектора в системе координат « », вращающейся с угловой скоростью 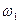, являются постоянными величинами.

Преобразуем уравнение (144) и приравняем действительные и мнимые части в правой и левой частях выражений (144) и получим два уравнения для модели АД с кз ротором при частотном управлении в форме структурной схемы.

. (152)

. (153)

Из уравнений (152) и (153) определим и .

. (154)

. (155)

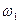Выражения позволяют построить структурную схему преобразования напряжения и частоты статора в фазные токи ротора и обобщенного АД при известных проекциях вектора потокосцепления статора , и частоты вращения ротора 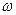. Но потокосцепление статора можно выразить через ток ротора с помощью выражения (141), преобразуя которое получим

. (156)

Представим комплексные векторы в выражении (156) в алгебраической форме в виде вещественных и мнимых составляющих и преобразуем уравнение (157), приравнивая действительные и мнимые части в правой и левой частях выражения (157). Получим с учетом того, что ,

. (157)

. (158)

. (159)

Из уравнения (158) определим , а решая уравнение (159), найдем .

. (160)

. (161)

Тогда, с учетом основного уравнения привода получим структурную схему АД. .

Структура АД нелинейная и имеет четыре перекрестные связи.

Упростить структуру АД для получения передаточных функций по каналам управления напряжением и частотой крайне затруднительно, но не представляет большого труда построить эту модель в системе Matlab/Simulink и получить требуемые характеристики привода при различных законах управления, связывающих какой-либо функцией входы управления частотой и напряжением статора.