Составим на основе полученной математической модели ДПТ с НВ в форме уравнений состояния математическую модель ДПТ с НВ в форме структурной схемы.

Рис. 2. Структурная схема математической модели ДПТ с НВ

Для того, чтобы реализовать два уравнения состояния в форме структурной схемы, необходимо использовать два интегратора. На входе первого интегратора действует сигнал, равный , а на его выходе сигнал равен . На входе второго интегратора действует сигнал, равный 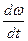, а на его выходе сигнал равен .

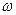В соответствии с уравнением (8) производная переменной состояния равна выражению . В этом математическом выражении величина постоянная, являющаяся параметром модели, а выражение в скобках включает координаты , и 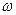уравнения состояния (8). В соответствии с правилами теории автоматического управления (ТАУ) для реализации на структурной схеме выражения необходимо на пропорциональное звено с передаточной функцией подать сигнал, равный . На выходе пропорционального звена (см. рис. 2) величина сигнала будет равна . Для определения выражения на структурной схеме системы электропривода с ДПТ с НВ используется узел сравнения (вычитатель), выполняющий операцию вычитания сигналов и из сигнала .

Реализация уравнения (9) в форме структурной схемы, соответствующей МЧ системы электропривода с ДПТ с НВ, рассмотрена в главе 7.

8.4. Преобразование структурной схемы модели электропривода с ДПТ НВ независимого возбуждения

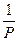Преобразуем структурную схему математической модели ДПТ с НВ, представленную на рис. 2. Для этого заменим звенья ( и 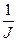) и ( и 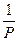) с последовательным соединением на этой структурной схеме звеньями с эквивалентными передаточными функциями и (см. рис 3).

Рис. 3. Структурная схема математической модели ДПТ с НВ после первого преобразования

Выполним еще одно преобразование полученной структурной схемы математической модели ДПТ с НВ на рис. 3. Для этого представим узел сравнения, реализующий операцию вычитания сигналов и из сигнала двумя узлами сравнения (см. рис. 4). Первый узел сравнения предназначен для вычитания сигнала из сигнала с результатом , а второй узел сравнения необходим для представления операции вычитания сигнала из сигнала .

Рис. 4. Структурная схема математической модели ДПТ с НВ после второго преобразования

Выполним третье преобразование полученной структурной схемы математической модели ДПТ с НВ на рис. 4. Для этого воспользуемся правилами преобразования структурных схем, известных в ТАУ (см. рис.5).

Рис. 5. Преобразование структурной схемы со звеном обратной связи

На рис. 5 представлена структурная схема, в которой звено с передаточной функцией охвачено звеном отрицательной обратной связи (ООС) с передаточной функцией .

, (10)

где - передаточная функция замкнутой системы автоматического управления (САУ);

- передаточная функция разомкнутой САУ;

- передаточная функция обратной связи;

В данном случае (см. рис. 4) , а . Тогда

, (11)

где .

Рис. 6. Структурная схема математической модели ДПТ с НВ после третьего преобразования

Структурная схема ДПТ с НВ на рис. 6 показывает, что электрический двигатель постоянного тока характеризуется отрицательной обратной связью (по эдс).

Выполним следующее преобразование полученной структурной схемы математической модели ДПТ с НВ на рис. 6, заменив два последовательно соединенных звена и одним эквивалентным звеном .

- коэффициент передачи ЭД.

Рис. 7. Структурная схема математической модели ДПТ с НВ после четвертого преобразования

Структурные схемы на рис. 6 и 7 представляют собой компактные математические модели ДПТ с НВ и легко реализуются стандартными программными продуктами.