Практическая работа 5. Транспортные задачи линейного программирования. Решение методом потенциалов

Цель: Ознакомить студентов с методикой постановки транспортных задач и методом потенциалов их решения.

В результате проработки темы студент должен научиться делать математическую постановку транспортных задач и освоить метод потенциалов для их решения.

Актуальность темы: Метод потенциалов отличается от других методов решения задач линейного программирования.

Теоретическая часть

В отличие от других задач линейного программирования (ЗЛП), транспортные задачи имеют такие особенности:

- распределяются между поставщиками и потребителями только однородные ресурсы;

- системой ограничений является система только строгих равенств;

- все переменные выражаются одними единицами измерения;

- матрицы коэффициентов в системах ограничений состоят из одних единиц;

- в системах ограничений каждая переменная встречается только дважды: один раз в ограничениях по поставкам и один раз в ограничениям по потребностям.

Эти особенности позволяют решать транспортные задачи более простым, чем симплекс-метод, методом потенциалов, хотя они могут быть решены и симплекс-методом.

Пример постановки транспортной задачи.

Задача

Имеется три пункта поставки однородного груза А₁, А₂, А₃ и четыре пункта потребления груза B₁, В₂, В₃, В₄. На пунктах А₁, А₂, А₃ находится груз соответственно в количестве 120; 80 и 640 тонн. В пункты B₁, В₂, В₃, В₄ требуется доставить соответс­твенно 100; 70; 50: 20 тонн груза. Затраты на перевозку 1 тонны гру­за между пунктами поставки и пунктами потребления приведены в матрице С (в тыс. руб.).

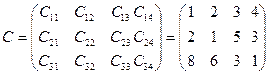, (1)

где C_ij – стоимость перевозки 1 тонны груза от поставщика с номе­ром i (i = 1; 2; 3) к потребителю с номером j (j = 1; 2; 3; 4). Найти такой план закрепления потребителей за поставщиками, чтобы общие затраты по перевозкам груза были минимальными.

Вначале сформулируем постановку задачи. Данные задачи запишем в виде матрицы (таблицы) перевозок .

Таблица 1.

Базы	Потребители	Запасы
B1	B2	В3	В4
A1	1	2	3	4
А2	2	1	5	3
А3	8	6	3	1
Потребности

В верхнем углу каждой клетки проставлены тарифы, взятые из матрицы С – технологической матрицы перевозок.

Тариф C_1j – это величина, равная (или пропорциональная) стои­мости перевозки единицы груза из данного пункта отправления A₁ в указанный пункт назначения В_j.

Введем переменные. Обозначим x_ij (тонн) – величину поставки от базы-поставщика i (i = 1,2,3) потребителю j (j = 1,2,3,4); Z (тыс. руб.) – общая стоимость всех перевозок. Матрица неизвестных { x_ij }, где i = 1,2,3; j = 1,2,3,4 называется планом перевозок. Очевидно, поставки 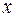_ij ³ 0, они вписы­ваются в клетки матрицы перевозок.

Нужно найти оптимальный план перевозок, такой, при котором об­щая стоимость перевозок Z – целевая функция – минимальна.

Проверяем сбалансированность данных задачи: сумма всех за-­
пасов (120+80+40)=240 равна сумме всех потребностей
(100+70+50+20)=240. Модель такой ЗЛП называется закры­той.

Замечание. Если модель ТЗЛП оказалась открытой, то ее «закры­вают» введением фиктивного поставщика или потребителя с недостаю­щим объемом груза и нулевыми тарифами.

Вписывая мысленно 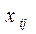в клетки таблицы , выпишем ограничения:

а) по запасам: 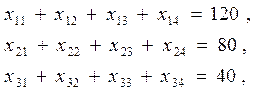(2)

б) по потребностям:

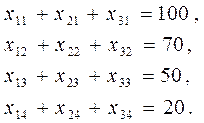(3)

Целевая функция имеет вид:

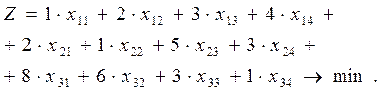(4)

Так как (2), (3), (4) – линейные соотношения, поставленная транспортная задача тоже является задачей линейного программирования.

Составление опорного плана

Составим первоначальный опорный план поставок методом ми­нимального тарифа по всей матрице перевозок. Просматривая тарифы
по всей матрице, находим наименьший. Их в таблице 4. 5 оказалось три:
С₁₁ = С₂₂ = С₃₄ = 1. Поэтому заполнение таблицы начнем с любой из
клеток: (1;1), (2;2) или (3:4). В каждую из клеток вписываем макси­мально возможную поставку с учетом запасов и потребностей. Ставим в клетку (1.1) поставку, равную 100, в клетку (2,2) – поставку 70 и в клетку (3,4) – поставку 20.

Ищем в матрице следующие по величине тарифы. В клетке (1,2) С₁₂ =2, но поставку сюда ставить нельзя, т. к. потребности B₂ полностью удовлетворены. То же самое можно сказать и о клетке (2,1), где С₂₁ = 2. Далее отыскиваем С₂₃ = С₂₄ = С₃₃ = 3. В клет­ку (1,3) ставим поставку 20, т. к. в запасе у поставщика А₁ оста­лось 20 единиц груза. В клетку (3,3) ставим поставку 20, т. к. у поставщика А₃ осталось всего 20 единиц груза. В клетку (2,4) пос­тавку ставить нельзя, т. к. спрос потребителя В₄ удовлетворен пол­ностью. Остается неудовлетворенным спрос потребителя В₃ в размере 10 единиц. Эту поставку ставим в клетку (2,3), т. к. у поставщика А₂ есть в запасе необходимое количество груза.

Таблица 2.

Базы	Потребители	Запасы
β1 = 1 В1	β2 = -1 В2	β3 = 3 В3	β4 = 1 В4
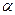1 =0; А1	10 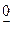1	2	20 + 3	4
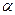2=0; А2	+ 2	70 1	10 - _ 5	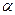3
3=0; А3	8	6	20 3	20 1
Потребности

Для контроля проверим сбалансированность поставок по всем строкам и столбцам (базам и потребителям): по первой строке (120 + 20) = 120, по второй строке (70 + 10) = 80 и т. д.

Подсчитаем количество заполненных клеток. Любо­му опорному плану должно соответствовать ровно (m + n - 1) запол­ненных клеток, где m – количество поставщиков (строк), n – коли­чество потребителей (столбцов). Если заполненных клеток окажется меньше, чем (m + n - 1), то такой план называется вырожденным. В нашей задаче m + n-l = 3 + 4-l=6, где m = 3 – коли­чество поставщиков, n = 4 – количество потребителей. Заполненных клеток в таблице 4.6 также оказалось 6, следова­тельно, план невырожденный.

Замечание. Если план окажется вырожденным, т. е. заполненных клеток будет меньше чем 6, то их количество нужно довести до 6, проставляя в некоторые пустые клетки нулевые поставки. Желательно помещать нулевую поставку в клетку с наименьшим тарифом, но при этом обязательно так, чтобы она не образовала с ранее заполненны­ми клетками замкнутого цикла (понятие «цикл» см. ниже). В резуль­тате заполненных клеток должно оказаться ровно (m + n - 1).

В итоге приходим к первому опорному плану, помещенному в таб­лице 4.6. Из таблицы видно, что x₁₁ = 100; x₁₃ = 20; x₂₂ = 70; x₂₃ = 10; x₃₃ = 20; x₃₄ = 20.

Пустым клеткам соответствуют переменные x_ij, равные нулю, что указывает на отсутствие поставок.

Стоимость перевозок, соответствующая первому опорному плану, определяется с помощью тарифов:

Z = 1∙100 + 3∙20 + 1∙70 + 5∙10 + 3∙20 + 1∙20 = 360 (тыс. руб.)

Другим методом составления первого опорного плана является

метод северо-западного угла, когда заполнение матрицы перевозок начинается с клетки (1;1), куда вписывается максимально возможная поставка, а затем заполняется соседняя клетка по строке или столбцу, в зависимости от запасов и потребностей груза, и т. д., пока не дойдем до последней клетки. Для нашей задачи это был бы план:

Таблица 3.

Базы	Потребители	Запасы
В1	В2	В3	В4
А1	100 1	20 2	3	4
А2	2	50 1	30 5	3
А3	8	6	20 3	20 1
Потребности

Этот метод не учитывает тарифов перевозок, и поэтому получа­ется, как правило, план, далекий от оптимального. В частности, указанный план дает стоимость перевозок Z = 420 тыс. руб. Свое название описанный метод получил оттого, что положение клетки (1;1) соответствует северо-западу на географической карте.