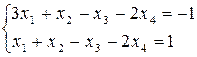Системы линейных алгебраических уравнений и методы их решения
Рассмотрим систему m линейных уравнений с n неизвестными.
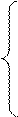 | a11x1 + a12x2 +… + a1nxn = b1, a21x1 + a22x2 +… + a2nxn = b2, ………………………………………………. am1x1 + am2x2 +… + amnxn = bm. |
(7)
Теорема Кронекера-Капелли. Для того, чтобы система m линейных алгебраических уравнений с n неизвестными была совместна, необходимо и достаточно, чтобы ранг ее основной матрицы A был равен рангу расширенной матрицы B, rang A = rang B = r, где
A = 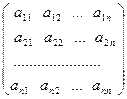 , B =
, B = 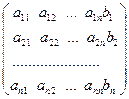 . (8)
. (8)
Если r = n, то система имеет единственное решение, если r < n система имеет бесконечное множество решений, зависящее от n – r произвольных параметров.
Если в системе (7) все свободные члены равны нулю, система называется однородной, в противном случае – неоднородной. Так как для однородной системы rang A = rang B, она всегда совместна.
1. Метод Крамера решения систем n линейных уравнений с n неизвестными состоит в отыскании неизвестных по формуле Крамера
xi = 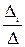 (i = 1, 2, 3, … , n) , (9)
(i = 1, 2, 3, … , n) , (9)
где Δ – основной определитель системы, а определители Δi представляют собой определители того же порядка, которые получены из основного путем замены в нем i-го столбца столбцом свободных членов системы.
2. Матричный метод решает также систему n уравнений с n неизвестными, для которой матрица коэффициентов является невырожденной. Тогда для A существует обратная матрица A–1.
Заданную систему уравнений
 | a11x1 + a12x2 +… + a1nxn = b1, a21x1 + a22x2 +… + a2nxn = b2, ……………………………. (10) an1x1 + an2x2 +… + annxn = bn. , если обозначить B = 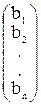 ; X = ; X =  , , |
можно записать в матричном виде:
A · X = B, A–1 · A · X = A–1 · B, X = A–1 · B, (11)
где введены в рассмотрение матрицы–столбцы для свободных членов и неизвестных. Умножая матричное уравнение на обратную матрицу A–1 слева, получим матрицу-столбец, дающую решение системы.
Пример 1
Решить методом Крамера систему
 | 4x2 + 4x3 = –19, 2x1 – 3x2 – 5x3 = –5, –3x1 – 2x2 – 3x3 = 2. |
Решение системы имеет вид x1 = 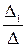 ; x2 =
; x2 = 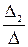 ; x3 =
; x3 = 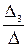 .
.
Вычислим определители Δ = 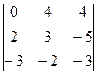 = 32; Δ1 =
= 32; Δ1 = 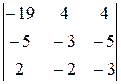 = –17;
= –17;
Δ2 = 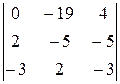 = –443; Δ3 =
= –443; Δ3 = 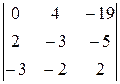 = 291;
= 291;
x1 = 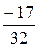 ; x2 =
; x2 = 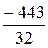 ; x3 =
; x3 = 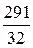 .
.
Пример 2
Данную систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы:
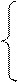 | x1 + 5x2 – x3 = 3 2x1 + 4x2 – 3x3 = 2 3x1 – x2 – 3x3 = –7. |
Решение
Обозначим через A – матрицу коэффициентов при неизвестных; X – матрицу-столбец неизвестных x1, x2, x3; B – матрицу-столбец свободных членов:
A = 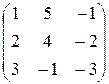 ; X =
; X = 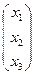 ; B =
; B = 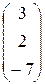 .
.
С учетом этих обозначений данная система уравнений принимает следующую матричную форму:
A · X = B .
Если матрица A – невырожденная (ее определитель Δ отличен от нуля), то она имеет обратную матрицу A–1. Умножив обе части уравнения на A–1 слева, получим:
A–1 · A · X = A–1 · B .
Но A–1 · A = E (E – единичная матрица), а E · X = X, поэтому
X = A–1 · B .
Это равенство называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу A–1.
Пусть имеем невырожденную матрицу
A = 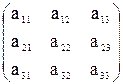 , тогда A-1=
, тогда A-1= 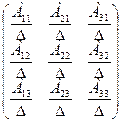 ,
,
где Aij (i = 1, 2, 3; j = 1, 2, 3) – алгебраические дополнения для элементов aij в определителе матрицы A.
Вычислим определитель Δ и алгебраические дополнения Aij элементов матрицы A.
Δ = 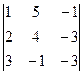 = –16 ≠ 0, следовательно, матрица A имеет обратную матрицу A–1.
= –16 ≠ 0, следовательно, матрица A имеет обратную матрицу A–1.
A11 = 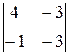 = –15; = –15; | A21 = – 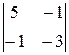 = 16; = 16; |
A31 = 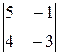 = –11; = –11; | A12 = – 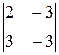 = –3; = –3; |
A22 = 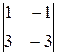 = 0; = 0; | A32 = – 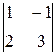 = 1; = 1; |
A13 = 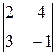 = –14; = –14; | A23 = – 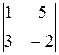 = 16; = 16; |
A33 = 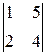 = –6; = –6; |
Тогда A–1 = 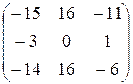 ·
· 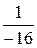
Находим решение данной системы уравнений в матричной форме:
X = 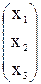 = –
= – 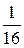 ·
· 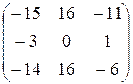 ·
·  =
= 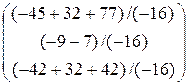 = =
= = 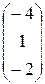 .
.
Отсюда x1 = –4; x2 = 1; x3 = –2.
3. Метод Жордана-Гауссаили метод последовательных исключений является наиболее универсальным по сравнению с предыдущими методами решения систем линейных алгебраических уравнений, так как позволяет решать и системы m линейных уравнений с n неизвестными, когда основная матрица A системы имеет ранг r 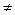 n. Тогда расширенная матрица системы путем элементарных преобразований может быть приведена к виду
n. Тогда расширенная матрица системы путем элементарных преобразований может быть приведена к виду
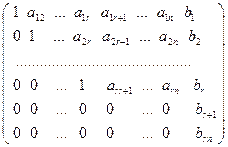 , (12)
, (12)
т. е. исходная система уравнений к виду:
| x1 + a12x2 + … + a1rxr + a1r+1xr+1 + … + a1nxn = b1 x2 + … + a2rxr + a2r+1xr+1 + … + a2nxn = b2 ………………………………………….. xr +arr+1xr+1 + … + arnxn = br 0 = br+1 0 = brn . (13) |
Если хотя бы одно из чисел br+1= … = brn не равно нулю, система не имеет решений. Если br+1= … = brn = 0, система совместна, из нее можно последовательно выразить в явном виде базисные неизвестные xr, xr–1, … , x2, x1 через свободные, число которых (n – r): xr+1, … , xn .
В случае r = n решение этой системы единственно, и все неизвестные последовательно выражаются из последней системы снизу вверх.
Пример 1
 Методом Жордана-Гаусса решить систему:
Методом Жордана-Гаусса решить систему:
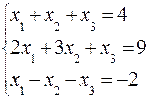 . (14)
. (14)
Так как  =
= 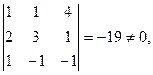 система имеет единственное решение.
система имеет единственное решение.
Прямой ход. Умножаем первое уравнение сначала на (-2) и складываем со вторым, затем первое на (-1) и складываем с третьим. Получим
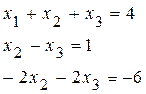
Третье уравнение можно сократить на (+2), а потом третье уравнение сложить со вторым. Получим треугольную систему:
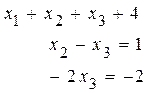 . (15)
. (15)
Заметим, что прямой ход преобразований системы (14) соответствует приведению расширенной матрицы коэффициентов системы к треугольному виду методом Гаусса. Подчеркиваем разрешающий ведущий элемент, ведущую строку умножаем на (-2), (-1).
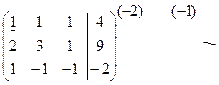
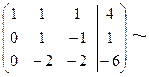
и складываем со второй и третьей строками соответственно, получая нули сначала в первом столбце под диагональным элементом. Потом ведущей считаем вторую строку и подчеркиваем разрешающий элемент, складываем ее с третьей строкой.
~ 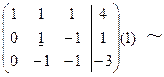
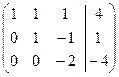 .
.
Получили треугольную матрицу. Из нее получим треугольную систему
(15).
Обратный ход. Из последнего уравнения определяем 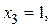 из второго находим
из второго находим 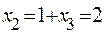 , из первого
, из первого 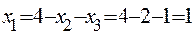 . Решение системы
. Решение системы 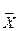 = (1; 2; 1).
= (1; 2; 1).
Пример 2
Найти одно из базисных решений системы:
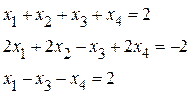 .
.
Так как в системе содержится 3 уравнения и 4 неизвестных, система либо имеет бесчисленное множество решений, либо несовместна. Найдем ранг системы. Составим расширенную матрицу системы и будем приводить ее к треугольному виду методом Гаусса:
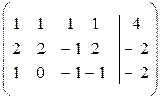 . (16)
. (16)
Так как 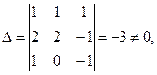 ранг матрицы r =3, поэтому три неизвестных
ранг матрицы r =3, поэтому три неизвестных 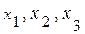 можно выбрать базисными, тогда
можно выбрать базисными, тогда 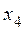 будет свободной. Обозначим ее через
будет свободной. Обозначим ее через 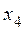 =С, перенесем в правые части уравнений, тогда система приобретает вид:
=С, перенесем в правые части уравнений, тогда система приобретает вид:
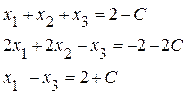 (17)
(17)
и решается так же, как система (5.3).
Приведем матрицу системы к диагональному виду:
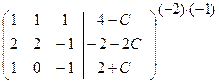
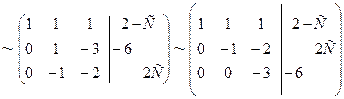 .
.
На последнем этапе поменяли 2 и 3 строку местами. Получим треугольную систему:
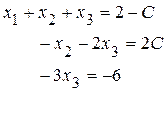 .
.
Обратным ходом найдем решение системы:
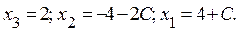
Таким образом, мы получим бесчисленное множество решений, называемое общим решением системы.
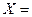 (4+C; -4-2C; 2; C) ,
(4+C; -4-2C; 2; C) ,
где С – произвольная постоянная.
Если положить свободную переменную 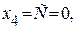 получим одно из базисных решений (базис) системы:
получим одно из базисных решений (базис) системы:
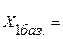 (4; -4; 2; 0).
(4; -4; 2; 0).
Заметим, что в качестве базисных можно было выбрать другие неизвестные, например, 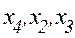 тогда
тогда 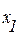 была бы свободной, и получили бы другое базисное решение.
была бы свободной, и получили бы другое базисное решение.
Замечание: Очевидно, что можно сразу приводить матрицу системы к диагональному виду (13), не перенося заранее свободные переменные в правые части уравнений.
Пример 3
С двух заводов поставляются автомобили для двух автохозяйств, потребности которых составляют 200 и 300 автомобилей. Первый завод выпустил 350 машин, второй – 150. Затраты на перевозку машин с завода в каждое автохозяйство приведены в таблице.
| Заводы | Затраты на перевозку в ден. ед. | |
| I | II | |
Минимальные затраты на перевозку составляют 7950 ден. ед.
Найти оптимальный план перевозок машин.
Решение.
Для постановки задачи составим балансовую таблицу, в уголки ячеек которой внесем технологические коэффициенты задачи и впишем переменные задачи xij – количество машин, поставляемых i – м заводом j – автохозяйству (i,j=1.2).
| Заводы | Автохозяйства | Выпуск | |
| I | II | ||
| x11 15 | x12 20 | ||
| x21 8 | x22 25 | ||
| Потребности |
Итак нужно найти матрицу неизвестных X = 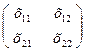 , элементы которой удовлетворяют ограничениям:
, элементы которой удовлетворяют ограничениям:
а) по выпуску автомобилей:
х11+х12=350
х21+х22=150
б) по потребностям автохозяйств:
х11+х12=200
х21+х22=300
в) цель задачи – обеспечить минимальные затраты на перевозку в размере 7950 д.е., в соответствии с технологией перевозок:
15х11=20х12+8х21=25х22=7950.
Получим систему 5 уравнений с четырьмя неизвестными
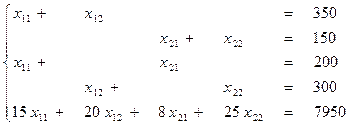
Решим систему методом Гаусса.
Преобразуем расширенную матрицу системы к треугольному виду. Для этого сначала переставим 4-ю строку на место 2-ой, 2-ую на место 3-ей, доставляя нули в первом столбце.
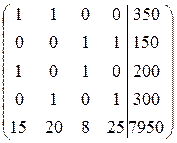 ~
~ 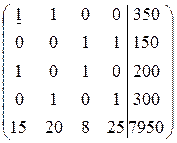
Вычтем из 4-ой строки первую, потом из 5-ой – первую, умноженную на (+15).
~ 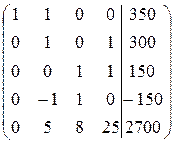 ~
~
Разрешающим элементом возьмем а22=1, четвертую строку сложим со второй, пятую сложим со второй, умноженной на (-5):
~ 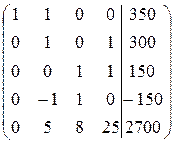 ~
~ 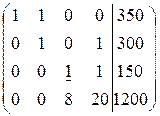 ~
~
Видим, что третья и четвертая строки оказались одинаковыми (это означает, что ранг системы равен 4, одно из уравнений лишнее). Вычеркнем одну из них. Выберем теперь разрешающей строкой третью, умножим ее на (-8) и сложим с последней.
~ 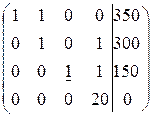 .
.
Получаем систему: 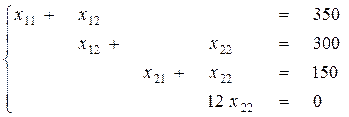
Обратным ходом снизу вверх получаем ответ:
х22=0; х21=150; х12=300; х11=50.
Пример 4.
Найти все возможные группы основных (базисных) переменных в системе
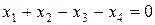
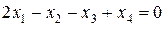
Решение. Общее число групп основных переменных не более чем 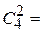
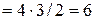 , т.е. возможные группы основных переменных:
, т.е. возможные группы основных переменных: 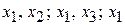 ,
, 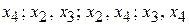 .
.
Выясним, могут ли быть основными переменные 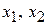 . Так как определитель матрицы из коэффициентов при этих переменных равен -3
. Так как определитель матрицы из коэффициентов при этих переменных равен -3 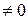 , то
, то 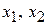 могут быть основными переменными. Рассуждая аналогично, найдем, что могут быть основными переменные
могут быть основными переменными. Рассуждая аналогично, найдем, что могут быть основными переменные 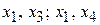 ;
; 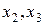 ;
; 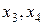 , но не могут быть основными
, но не могут быть основными 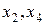 , так как соответствующий определитель при них равен нулю.
, так как соответствующий определитель при них равен нулю.
Пример 5. (ЭУК, глава 48)
Решить систему уравнений
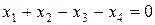
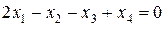
Решение.
В задаче 1 установлено, что основными могут быть переменные 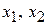 ;
; 
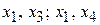 ;
; 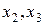 ;
; 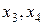 . Возьмем в качестве основных (базисных) переменные
. Возьмем в качестве основных (базисных) переменные 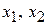 , а переменные
, а переменные 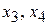 будем считать неосновными (совбодными) и перенесем их с соответствующими коэффициентами в правые части уравнений системы. Получим
будем считать неосновными (совбодными) и перенесем их с соответствующими коэффициентами в правые части уравнений системы. Получим
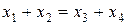
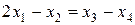
Решая данную систему любым способом, найдем 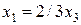 ;
; 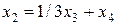 . Задавая неосновным (свободным) переменным
. Задавая неосновным (свободным) переменным 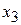 и
и 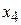 произвольные значения
произвольные значения 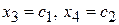 , получим бесконечное множество решений этой системы (
, получим бесконечное множество решений этой системы ( 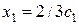 ;
; 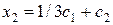 ;
; 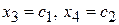 ).
).
Задание к практическому занятию:
Повышенный уровень:
Задача 5.
Решить систему уравнений в виде вектора 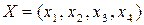 , где основными переменными будут х1 и х2, а две другие - свободными с1 и с2 , где с1 и с2 , – произвольные постоянные.
, где основными переменными будут х1 и х2, а две другие - свободными с1 и с2 , где с1 и с2 , – произвольные постоянные.
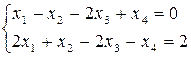
Ответ: 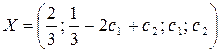
Задача 6
Решить систему уравнений в виде вектора 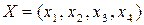 , где основными переменными будут х1 и х2, а две другие - свободными с1 и с2 , где с1 и с2 , – произвольные постоянные.
, где основными переменными будут х1 и х2, а две другие - свободными с1 и с2 , где с1 и с2 , – произвольные постоянные.
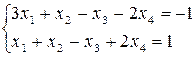
Ответ: 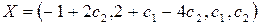
Задача 7.
Решить систему уравнений в виде вектора 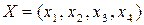 , где основными переменными будут х1 и х4, , а две другие - свободными с1 и с2 , где с1 и с2 , – произвольные постоянные.
, где основными переменными будут х1 и х4, , а две другие - свободными с1 и с2 , где с1 и с2 , – произвольные постоянные.
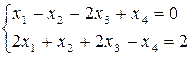
Задача 8.
Решить систему уравнений в виде вектора 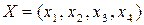 , где основными переменными будут х1 и х3, а две другие - свободными с1 и с2 , где с1 и с2 , – произвольные постоянные.
, где основными переменными будут х1 и х3, а две другие - свободными с1 и с2 , где с1 и с2 , – произвольные постоянные.
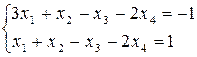
Задача 9.
Решить систему уравнений в виде вектора 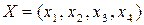 , где основными переменными будут будут х1 и х4, а две другие - свободными с1 и с2 , где с1 и с2 , – произвольные постоянные.
, где основными переменными будут будут х1 и х4, а две другие - свободными с1 и с2 , где с1 и с2 , – произвольные постоянные.