Текст программного модуля расчета нч arc-фильтра

Рис. 9.60 Полюса и нули

Рис. 9.61 Коэффициент передачи фильтра

Рис. 9.62 Затухание фильтра

Рис 9.63 Модуль коэффициента передачи фильтра

Глава 10. СИНТЕЗ ЛИНЕЙНЫХ АНТЕННЫХ СИСТЕМ

В этой главе будут рассматриваться простейшие линейные излучающие системы. Под линейной излучающей системой будет пониматься непрерывное или дискретное распределение одинаковых источников электромагнитного поля (т.е. излучателей), вдоль заданного направления в пространстве (рис.10.1). Примерами таких излучателей могут быть: длинный прямолинейный провод, щели в экране или в стенках волновода, диэлектрический стержень, система одинаковых излучателей (напр. вибраторов), спиральная антенна и т.д. Продольный размер излучателя может быть произвольным, а поперечные размеры, как правило, меньше длины волны. Как правило, комплексная характеристика направленности одного элемента излучателя известна.

Рис.10.1 Линейные излучатели

Общая постановка задачи

Задача синтеза антенны, или обратная задача электродинамики, возникает тогда, когда необходимо определить размеры, форму амплитуды и фазы возбуждающего тока или поля в раскрыве антенны по заданной диаграмме направленности. Например: получить узкую ДН при малых размерах самой антенны или получить узкую ДН при заданном уровне боковых лепестков. Могут так же синтезироваться антенны по максимальному КНД и оптимальной форме диаграммы направленности.

Требуемая диаграмма направленности задается в виде известной комплексной функции и ищется функция распределения возбуждения в ограниченной объеме пространства, которая обеспечивает характеристику направленности , близкую к заданной функции по определенным критериям. На практике получили наибольшее распространения два критерия близости этих функций: среднеквадратичный и равномерный. В случае среднеквадратичного приближения ошибка синтеза оценивается выражением:

(10.1)

и добиваются ее минимума подбором соответствующего возбуждения. Такое приближение используют, когда направленные свойства антенны усредняются по мощностным параметрам. Недостатком этого приближения является возможность появления локальных минимумов при синтезе функции .

При равномерном приближении ошибку синтеза определяют выражением:

,

которые представляют собой максимальное значение модуля отклонения полученной характеристики от заданной функции направленности. Минимизируются величины ошибки, причем изменение распределения возбуждения позволяет добиться требуемой близости функций и . Однако вычисление Δ, связано с нахождением максимума ошибки синтезируемой диаграммы направленности, поэтому является более сложным. Следовательно и решение задачи синтеза ДН в равноволновом приближении будет более сложным, чем при среднеквадратичном.

Ослабление этих трудностей возможно, если в выражение (10.1) показатель степени выбирать в диапазоне (n = 6 ÷ 10).

Решение задачи антенной системы заканчивается определением закона распределения возбуждения вдоль излучателя. Но после этого возникает задача реализации этого закона в виде конкретной конструкции излучателя и распределителя. Из-за возникающих дополнительных трудностей, при решении внутренних электродинамических задач антенн, этот этап, чаще всего, решается путем эксперимента.

При синтезе антенн обычно форма излучающей системы задается заранее:

· вид характеристики направленности сразу же может определить геометрию;

· условия работы антенны, состав той системы, в которой предполагается использование антенны;

· выбор формы антенны упрощает решение задачи синтеза, уменьшив тем самым число неизвестных.

Усложнение формы антенны, как правило, не требует разработки новых методов синтеза, а только обобщение уже имеющихся, поэтому дальше будем рассматривать теорию синтеза антенн, применительно к линейным излучающим системам.

Пусть на участке оси (х) расположен линейный излучатель с координатами от –L/2 до +L/2. Множитель направленности, которого может быть записан следующим образом [1]:

(10.2)

где - закон возбуждения вдоль излучателя; k=2π/λ;

функция - задана. Будем полагать, что в плоскости угла θ необходимая диаграмма направленности уже обеспечена правильным выбором элементов из которых состоит сама антенна.

Обозначим , и введем новую угловую переменную

(10.3)

Тогда уравнение (10.2) перепишется в виде

(10.4)

где 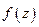определена только в области действительных углов –k ≤ z ≤ k, или .

В выражении (10.4) неизвестна функция , а само выражение называется неоднородным интегральным уравнением Фредгольма первого рода. При этом множитель представляет собой ядро этого уравнения. Особенностью данного уравнения является то, что сколько угодно малым изменением функции 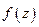могут соответствовать сколь угодно большие отличия в функции возбуждения вдоль излучателя . Это означает, что решение уравнения (10.4) может быть неустойчивым. Для получения устойчивых решений, необходимо ограничить поиск требуемого решения некоторыми дополнительными условиями, которые определяются какими либо физическими соображениями. Например: можно потребовать, чтобы среднее значение амплитуды возбуждения и средняя скорость изменения возбуждения были бы ограничены по сравнению с мощностью излучения. Эти ограничения можно записать математически следующим образом:

(10.5)

Здесь А и В некоторые заданные постоянные.