Синтез нерекурсивного фильтра методом частотной выборки
В методе частотной выборки импульсная характеристика фильтра h(n) находится путем дискретизации по частоте заданной частотной характеристики Hid(jω) и вычисления ее обратного дискретного преобразования Фурье (ОДПФ).
Дискретизация частотной характеристики Hid(jω) по частоте осуществляется в полосе 0 . . . ωд путем перехода от непрерывных значений частоты ω к дискретным: ωn = Δω·n, где n = 0, 1, . . ., N-1; 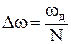 - шаг дискретизации; n – номер частотной выборки; N – число точек дискретизации.
- шаг дискретизации; n – номер частотной выборки; N – число точек дискретизации.
Шаг дискретизации по частоте Δω выбирается из условия 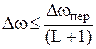 , где L – целые числа, L = 0, 1, 2, . . .; Δωпер – переходная полоса синтезируемого фильтра.
, где L – целые числа, L = 0, 1, 2, . . .; Δωпер – переходная полоса синтезируемого фильтра.
В результате получается дискретизированная частотная характеристика фильтра (ДЧХ) 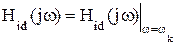 (Рис. 9.36).Так как заданная идеализированная частотная характеристика соответствует физически нереализуемому фильтру, то для ЦФ со ступенчатообразными АЧХ дискретизированная частотная характеристика отождествляется далее с их дискретизированной АЧХ.
(Рис. 9.36).Так как заданная идеализированная частотная характеристика соответствует физически нереализуемому фильтру, то для ЦФ со ступенчатообразными АЧХ дискретизированная частотная характеристика отождествляется далее с их дискретизированной АЧХ.
Дискретизация частотной характеристики на рис.9.36 выполнена с шагом 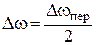 , (L = 1).
, (L = 1).
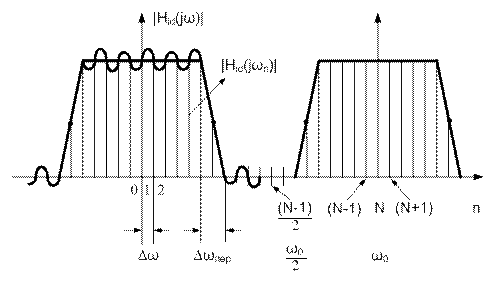
Рис. 9.36 Дискретизированная ЧХ цифрового фильтра нижних частот
ДЧХ имеет значения, равные в полосе пропускания 1 (Hid(jωn) = 1), в полосе задерживания – нулю (Hid(jωn) = 0) и в переходной полосе – некоторым промежуточным варьируемым значениям Hid(jωn) = var,от которых зависит качество аппроксимации в переходной полосе - некоторым лосе задерживания - нулю со ступенчатообразным заданной частотной характеристики.
ДЧХ Hid(jωn) можно поставить в соответствие некоторую импульсную характеристику hp(n), определяемую с помощью обратного дискретного преобразования Фурье (ОДПФ), получаемого путем дискретизации по частоте общего выражения для импульсной характеристики hid(n) соответствующей заданной (непрерывной) частотной характеристике Hid(jω):
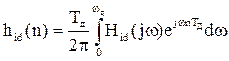
Выполняя замены:
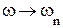 ;
; 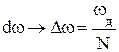 ;
; 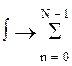 ,
,
получим импульсную характеристику hp(n):
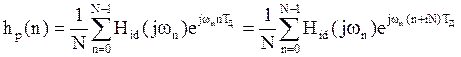
где i = 0, ±1, ±2, ±… .
В качестве импульсной характеристики синтезируемого методом частотной выборки НФ выбирается один период импульсной характеристики hp(n), сдвинутый вправо на 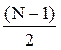 отсчетов (для обеспечения физической реализуемости) и усеченный прямоугольной весовой функцией (для получения КИХ – фильтра) (рис. 9.37).
отсчетов (для обеспечения физической реализуемости) и усеченный прямоугольной весовой функцией (для получения КИХ – фильтра) (рис. 9.37).
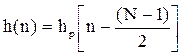 ,
,
n = 0, . . ., N – 1.
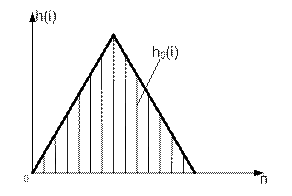
Рис. 9.37 Импульсная характеристика НФ, синтезированного методом частотной выборки
По импульсной характеристике h(n) находится частотная характеристика фильтра Hp(jω), аппроксимирующая заданную:
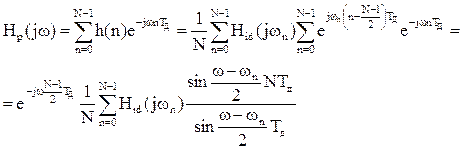
Это уравнение получено на основе выражения для суммы конечного числа членов геометрической прогрессии.
В этом выражении множитель 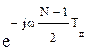 определяет ФЧХ фильтра, которая строго линейна вследствие симметрии импульсной характеристики.
определяет ФЧХ фильтра, которая строго линейна вследствие симметрии импульсной характеристики.
АЧХ фильтра на частотах 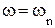 :
: 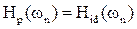 точно совпадает с частотными выборками ДЧХ, а на частотах
точно совпадает с частотными выборками ДЧХ, а на частотах 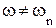 :
: 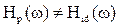 - отличается от заданной на величину погрешности аппроксимации.
- отличается от заданной на величину погрешности аппроксимации.
С учетом свойств четности АЧХ: 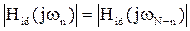 и нечетной симметрии ФЧХ: φ(ωn) =-φ(ωN-n) выражение для частотной характеристики фильтра может быть преобразовано к более удобному для расчетов виду:
и нечетной симметрии ФЧХ: φ(ωn) =-φ(ωN-n) выражение для частотной характеристики фильтра может быть преобразовано к более удобному для расчетов виду:
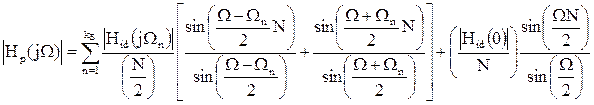
Здесь Ω = ωТд. Верхний предел суммирования 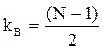 – при нечетном N и
– при нечетном N и 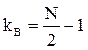 - при четном. В случае четного N для фильтра с линейной ФЧХ выполняется условие
- при четном. В случае четного N для фильтра с линейной ФЧХ выполняется условие 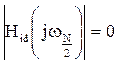 ,
, 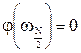 .
.
Качество аппроксимации в данном методе зависит от числа выборок частотной характеристики в переходной полосе L и их значений vari, (i = 1, 2, …, L) делающих аппроксимируемую функцию более гладкой. Различным значениям соответствуют следующие примерные значения максимального уровня боковых лепестков:
L = 0: aзmax ≈ – 20 дБ;
L = 1: aзmax ≈ – 40 дБ;
L = 2: aзmax ≈ – 50 – 60 дБ;
L = 3: aзmax ≈ – 80 – 100 дБ.
Реально методом частотной выборки можно синтезировать НФ с минимальным затуханием в полосе задерживания до (90 – 120) дБ.
Таким образом, оптимизация фильтра заключается в выборе L – числа выборок в переходной полосе и поиске их оптимальных значений variopt минимизирующих погрешности аппроксимации. Очевидно, что с увеличением числа варьируемых выборок существенно усложняется процедура оптимизации. Она достаточно эффективно реализуется на ЭВМ методом линейного программирования.
