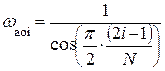Синтез аналогового фильтра прототипа

Синтез АФПНЧ включает выбор аппроксимирующей функции, определение порядка фильтра N, значений нулей p_оi и полюсов p_pi передаточной функции по заданным граничным частотам ω_ac = 1, ω_aз и допускам на погрешности аппроксимации a_n, a_з. Нули и полюсы синтезируемого АФПНЧ полностью определяют его передаточную функцию H(p):

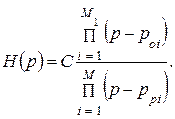
Здесь С – нормирующий множитель; M₁ – число полюсных нулей (M₁<M); M – число конечных полюсов. При этом полюсы являются вещественными или комплексно-сопряженными числами (со знаком минус перед реальной частью), а конечные нули часто мнимыми.

АЧХ фильтра прототипа H(jω_a) при синтезе задается выражением:

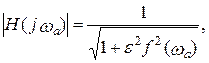
здесь ε² – параметр характеризующей неравномерность АЧХ в полосе пропускания 0<ω_a<1; f(ω_a) – аппроксимирующая функция или функция фильтрации. В полосе пропускания она должна стремиться к нулю, в полосе непропускания – к бесконечности. В качестве аппроксимирующих функций используются полиномы и дроби.

Кполиномиальным относятся аппроксимации Тейлора (фильтры Баттерворта), Чебышева, к дробным – Кауэра – Золоторева (эллиптические фильтры), Чебышева инверсная. Передаточные функции фильтров с полиномиальной аппроксимацией не имеют конечных нулей, их частотные характеристики монотонны в полосе задерживания. У фильтров с дробной аппроксимацией передаточные функции имеют нули на конечных частотах в полосе задерживания, а частотные характеристики – пульсации (в том числе равноволновые) в этой полосе. Фильтры Чебышева и эллиптические имеют равноволновые пульсации и в полосе пропускания.

Типичные графики частотных характеристик нормализованного АФПНЧ с полиномиальной и дробной аппроксимациями приведена на рис. 9.9.

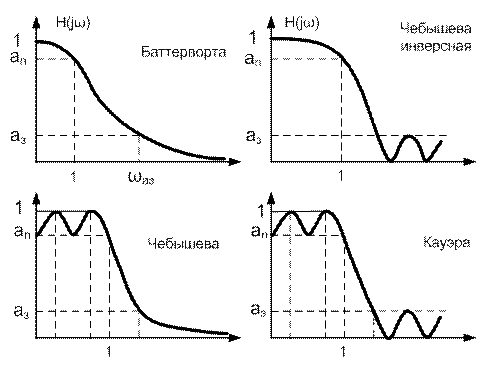
Рис. 9.9 АЧХ АФПНЧ соответствующее различным функциям

Расчет числа звеньев и определение полюсов и нулей низкочастотного фильтра прототипа

Фильтр Баттерворта

Неравномерность АЧХ фильтра в полосе пропускания (ПП) определяется по формуле:

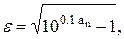
а порядок фильтра по формуле:

,

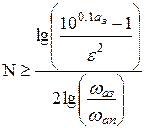и округляется до целого в сторону большего числа. Эта функция передачи не имеет нулей, а ее полюсы равномерно расположены в левой половине окружности единичного радиуса и определяются так:

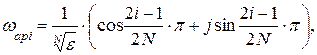
i = 0, 1, 2, …, 2N – 1

Фильтр Чебышева

Неравномерность АЧХ в полосе ПП связана с a_n следующей формулой:

a_n = 10lg(1 + ε²) , [дБ]

Число звеньев фильтра определяется так:

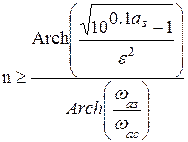
Функция передачи фильтра Чебышева также не имеет нулей, а ее полюсы расположены в левой половине эллипса на комплексной плоскости и определяются следующим образом:

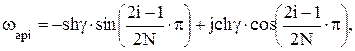
i = 1, 2, …, N,

Здесь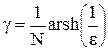

Фильтр Чебышева инверсный

Функция передачи фильтра Чебышева инверсного или фильтра Чебышева второго рода, в отличие от предыдущих, имеет нули и полюсы. АЧХ фильтра Чебышева второго рода описывается следующим выражением:

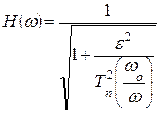
Здесь ω₀ – частота среза фильтра; T_n 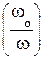– полином Чебышева n-ого порядка;

ε – параметр, определяющий величину пульсаций АЧХ в полосе задерживания a_з = 10lg(1 + ε²).

Полюса функции передачи фильтра – прототипа инверсного Чебышева определяется так [2]:

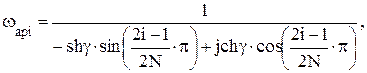
где 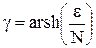, i = 1, 2, …, N.

Нули функции передачи являются мнимыми и могут быть найдены из решения уравнения Th 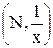= 0. Здесь Th 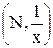– есть полином Чебышева N-го порядка, первого рода; х – параметр полинома, который может меняться в пределах ±∞. Эта функция встроена в вычислительную систему MathCAD и вызывается следующим образом: Tcheb (N, x), или по следующей формуле: