Стратегии одномерной оптимизации

Типы одномерных функций. Одномерная оптимизация относится к наиболее простому типу оптимизационных задач. Однако их более детальный анализ целесообразен, т.к. одномерные методы оптимизации часто используются в задачах, ориентированных на многомерные ситу­ации.

В инженерной практике приходится использовать как непрерывные, так и разрывные функции, в том числе и дискретные.

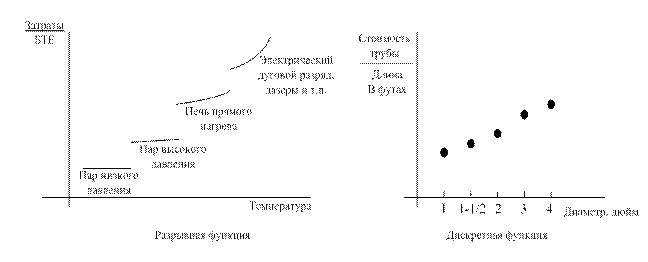
Рис. 6.44 Виды разрывных функций

Следует отметить, что метод, эффективный при анализе непрерывных функций, может оказаться неэффективным при исследовании разрывных функций, хотя обратное не исключается.

В дополнение к перечисленным выше свойствам можно также классифицировать функции в соответствии с их формой, определяющей топологические свойства функций в рассматриваемом интервале

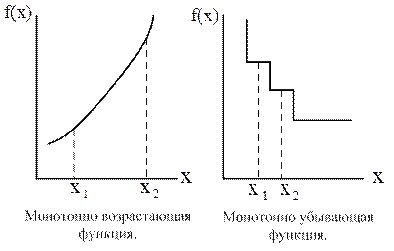
а) б)

Рис 6.45 Виды непрерывных функций

Монотонные функции. Функция f(х) является монотонной (как при возрастании, так и при убывании), если для двух произвольных точек х₁ и х₂, таких, что х₁ £ х₂, выполняется одно и следующих неравенств:

f(х₁)£ f(х₂) (монотонно возрастающая функция),

f(х₁)³ f(х₂) (монотонно убывающая функция).

На рис. 6.45 а представлен график, монотонно возрастающей функции а на рис. 6.45 б – график монотонно убывающей функции. Заметим, что монотонная функция не обязательно должна быть непрерывной. На рис. 6.46 изображен график функции, которая монотонно убывает при х£ 0 и монотонно возрастает при х ³ 0.

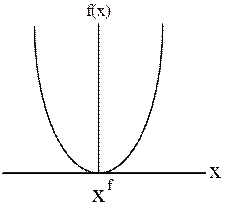
Рис. 6.46 Унимодальная функция

Определение:

Функция f(х) является унимодальной на отрезке а£ х £ в в том и только том случае, если она монотонна по обе стороны от единственной на рассматриваемом интервале оптимальной точке х*. Другими словами, если х* – единственная точка минимума f(х) на отрезке а£ х £ в, то f(х) оказывается унимодальной на данном интервале тогда и только тогда, когда для точек х₁ и х₂:

Из х* £ х₁ £ х₂ f(х*) £ f(х₁) £ f(х₂)

Из х* ³ х₁ ³ х₂ f(х*) £ f(х₁) £ f(х₂)

Рис. 6.47 Унимодальные функции

Как показано на рис. 6.47 унимодальная функция не обязательно должна быть непрерывной. Унимодальность функций являйся исключительно важным свойством, которое широко используется в оптимизационных исследованиях. Вопросы, связанные с этим свойством функций, рассматриваются ниже.

Критерии оптимальности. При анализе оптимизационных задач, как правило, возникают два общих вопроса.

1. Вопрос анализа «в статике». Как определить, представляет ли данная точка х* оптимальное решение задачи?

2. Вопрос анализа «в динамике» Если х* не является точкой оптимума, то какая последовательность действий приводит к получению оптимального решения?

В этом разделе основное внимание уделяется решению вопроса анализа «в статике», а именно построению множества критериев оптимальности, позволяющих определить, является ли данное ре­шение оптимальным.