Алгоритмы и примеры решения задач одномерной оптимизации
Новокузнецк
Министерство образования Российской Федерации
Сибирский государственный индустриальный университет
Кафедра информационных технологий в металлургии
АЛГОРИТМЫ И ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ
Методические указания к выполнению лабораторно-практических работ
по курсу «Оптимизация в технике и технологиях»
Специальности: «Информационные системы и технологии» (071900), специализации «Прикладное математическое и программное обеспечение»,
по курсу «Методы оптимизации в металлургии»
Специальности: «Металлургия черных металлов» (110100),
специализации «Информационные технологии и предпринимательство
в металлургии» (110107).
Новокузнецк
УДК 681.3.06
Алгоритмы и примеры решения задач одномерной оптимизации: Метод. указ./ Сост.: С.П Мочалов, И.А. Рыбенко.: СибГИУ.- Новокузнецк, 2004.- 18с., ил.
Изложены теоретические аспекты методов поиска экстремума функции одной переменной, представлены алгоритмы методов, приведены примеры решения задач одномерной оптимизации и варианты заданий.
Предназначены для студентов специальности «Информационные системы и технологии» (071900), специализации «Прикладное математическое и программное обеспечение» и «Металлургия черных металлов» (110100), специализации «Информационные технологии и предпринимательство в металлургии» (110107).
Рецензент - кафедра систем автоматизации (зав. кафедрой С.М.Кулаков)
Печатается по решению редакционно-издательского совета университета.
1. ОБЩИЕ ПОЛОЖЕНИЯ
В настоящем издании рассматривается решение наиболее простого типа задач оптимизации – поиск экстремума функции одной переменной. Данная задача формулируется как нахождение такого значения входной переменной объекта, которое соответствует наилучшему (минимальному или максимальному) значению целевой функции.
Хотя на практике задачи, в которых критерий задан функцией одной переменной, встречаются достаточно редко, анализ таких задач занимает центральное место в оптимизационных исследованиях. Это объясняется тем, что многие многомерные методы достаточно понятны, легко могут быть проиллюстрированы графически, что позволяет глубже понять сущность задач оптимизации и способствует приобретению навыков их решения.
Постановка задачи одномерной оптимизации заключается в нахождении точки х*, в которой целевая функция f(х*) принимает минимальное (максимальное) значение. Функция f(x) имеет локальный минимум в точке х0, если при e>0 существует окрестность [x-e; x+e ], такая, что для всех значений х в этой окрестности f(x) больше f(x*). Функция f(x) имеет глобальной минимум в точке х*, если для всех х справедливо неравенство f(x) >f(x*).
Аналитический анализ функции. Классический подход к задаче нахождения экстремума функции состоит в поиске условий, которым они должны удовлетворять. Необходимым условием экстремума в точке x* является равенство нулю первой производной, т.е. требуется решить уравнение f ’(x)=0.
Данному уравнению удовлетворяет как локальные и глобальные экстремумы, так и точки перегиба функции, поэтому приведенное условие является необходимым, но не достаточным.
С целью получения более определенных выводов требуется расчет значений вторых производных в точках, удовлетворяющих уравнению равенства нулю первой производной. При этом доказано, что минимуму функции соответствует положительной значение второй производной (f’”(x)>0), а максимальному – отрицательное (f’”(x)<0). Однако, если вторая производная равна нулю, ситуация остается неопределенной.
Классификация численных методов. Для определения экстремума функции одной переменной можно применять поисковые методы и методы с использованием производных. Среди методов поиска выделяют методы последовательного сокращения интервала (сканирования, локализации оптимума, половинного деления, золотого сечения, Фибоначчи) и методы точечного оценивания (Пауэлла, квадратичной аппроксимации, обратного переменного шага). На основе использования производных построены методы: средней точки, секущих, кубичной аппроксимации, Ньютона и др.
Целью выполнения лабораторно-практических работ является: формирование навыков решения оптимизационных задач с использованием различных методов поиска экстремума функции одной переменной.
2. ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ МЕТОДОВ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ. АЛГОРИТМЫ И ПРИМЕРЫ РЕШЕНИЯ.
2.1 Поисковые методы
Основой всех одномерных поисковых методов является сокращение интервала неопределенности, а именно: построение последовательности отрезков [ak ; bk], стягивающихся в точке х* - минимуму функции на исходном отрезке. Методы оптимизации отличаются друг от друга лишь различным выбором точек на начальном интервале неопределенности: в методе половинного деления – число Е>0 – наименьший сдвиг по х, при котором еще можно отличить f(x) и f(x+Е); в методе золотого сечения – величина 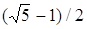 ; в методе Фибоначчи используются числа Фибоначчи.
; в методе Фибоначчи используются числа Фибоначчи.
Общая последовательность реализации методов такова: установление границ начального интервала, выбор точек в начальном интервале неопределенности; вычисление значений функции в этих точках и сравнение этих значений; проверка критерия окончания расчетов.
На этапе установления границ интервала на основе априорных данных или правил исключения строится относительно широкий интервал [a, b], содержащий точку оптимума x*. Обычно поиск граничных точек такого интервала проводится с помощью эвристических методов поиска, хотя в ряде случаев можно также использовать методы экстраполяции. Так как минимум x* на [a, b] неизвестен, то этот интервал называется интервалом неопределенности. Для унимодальной функции f(x) интервал неопределенности может быть сокращен с помощью вычисления значений функции в двух точках x, y Î [a, b]. При этом возможны два случая. Если f(x) > f(y), то новым интервалом неопределенности является [x, b], поэтому переприсвоение границ интервала на итерациях для этого случая осуществляется по правилу ak+1 = xk, а bk+1 = bk. При выполнении условия f(x) £ f(y), новым интервалом будет [a, y] и, соответственно, ak+1 = ak, bk+1 = yk.
2.1.1 Метод сканирования
Сканирование или равномерный поиск является примером одновременного поиска, когда точки, в которых вычисляется значение функции, выбираются заранее. Начальный интервал неопределенности [a1, b1] делится на отрезки величиной d сеткой из точек a1 + kd для k = 1, …, n. Тогда b1 = a1+ (n - 1)d. Затем функция f(x) вычисляется в каждой из n точек сетки и определяется 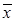 , в которой она имеет наименьшее значение. Если f(x) унимодальна, то минимум принадлежит интервалу [
, в которой она имеет наименьшее значение. Если f(x) унимодальна, то минимум принадлежит интервалу [ 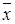 - d ,
- d , 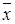 + d].
+ d].
После n вычислений функции интервал [a1, b1] сокращен до длины 2d. Так как n = [(b1 - a1)/d] - 1, то для достижения более высокой точности нахождения минимума необходимо большое число вычислений функции.
Алгоритм метода сканирования.
Начальный этап. Выбрать шаг разбиения d> 0 и начальный интервал [a1, b1]. Задать k = 1 и перейти к основному этапу.
Основной этап. Шаг 1. Вычислить значение х=a1 + kd и f(x). Если k=n, то перейти к шагу 2, иначе положить k=k+1 и вернуться к шагу 1.
Шаг 2. Выбрать минимальное значение функции f(x) и соответствующее ему значение 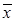 . Минимум функции находится в интервале [
. Минимум функции находится в интервале [ 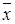 -d ,
-d , 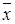 + d].
+ d].
