Связь теоремы Куна-Таккера с теорией игр и седловыми точками

Ещё раз посмотрим на всё это несколько с другой стороны. Рассмотрим функцию Лагранжа 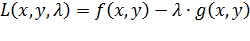для всех х≥0 и λ≥0, т. е. задача о максимизации f(х) соответствует задаче о седловой точке, иными словами, задаче о максимине для функции L(х, λ).

Теорема (о достаточных условиях экстремума).

Пусть 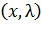– седловая точка функции Лагранжа 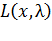в области 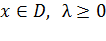. Тогда 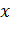является оптимальным планом, и выполняется условия дополняющей нежесткости: .

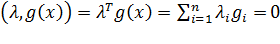Доказательство. По определению седловой точки для :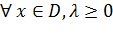

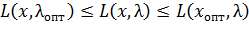, (3.7.1)

Из второго неравенства в (2.32) следует, что

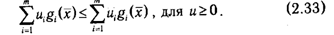
Однако (2.33) может иметь место только тогда, когда g_i(x)≤0 при всех i∊1:m. Действительно, если существует такое k, что g_k(x)>0, то, положив и_i=0 для всех i ≠ k и выбрав достаточно большое и_k > 0, можно добиться того, что значение

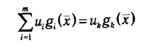
окажется больше постоянного выражения

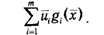
Из того, что для всех i∊1:m выполняются неравенства g_i(x)≤0, следует, что х является допустимым планом задачи (2.28).

Если в левую часть неравенства (2.33) подставить значения u_i = 0, i∊1:m, то получим, что

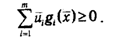
Вместе с тем из того что, g_i(x)≤0 и u_i ≥0, следует оценка

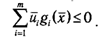
Совместное рассмотрение последних двух неравенств приводит к правилу дополняющей нежесткости в точке х:

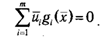
Тогда на основании левой части неравенства седловой точки (2.32) имеем, что для всех х∊Х (в том числе и для х∊D)

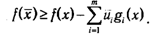
Но условию ЗНП для любых х∊D верны неравенства g_i(x)≤0, что, в сочетании с условием u_i ≥0, позволяет записать

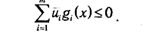
Значит,

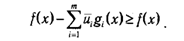
Окончательно получаем, что для любых х∊D справедливо соотношение (3.28)

f(x)≥f(x), ,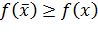

т. е. х - оптимальный план.

ЛИТЕРАТУРА

[1] Алексеев В. М., Тихомиров В. М., Фомин С. В., Оптимальное управление, Наука, М., 1979 MathSciNet MathSciNet

[2] Сухарев А. Г., Тимохов А. В., Федоров В. В., Курс методов оптимизации, Наука, М., 1986 MathSciNet MathSciNet Zentralblatt MATH

[3] Васильев Ф. П., Методы оптимизации, В 2-х кн., МЦНМО, М., 2011

[4] Мину М., Математическое программирование. Теория и алгоритмы, Наука, М., 1990 MathSciNet MathSciNet

[5] Обен Ж.-П., Нелинейный анализ и его экономические приложения, Мир, М., 1988 MathSciNet MathSciNet

[6] Обен Ж.-П., Экланд И., Прикладной нелинейный анализ, Мир, М., 1988 MathSciNet MathSciNet

[7] Сумин М. И., “Регуляризованная параметрическая теорема Куна–Таккера в гиль- бертовом пространстве”, Ж. вычисл. матем. и матем. физ., 51:9 (2011), 1594– 1615 Math-Net.Ru MathSciNet MathSciNet Zentralblatt MATH

[8] Sumin M. I., “On the stable sequential Kuhn–Tucker theorem and its applications”, Appl. Math., 3:10A, Special issue “Optimization” (2012), 1334–1350

[9] Сумин М. И., “Оптимальное управление параболическими уравнениями: двой- ственные численные методы, регуляризация”, Распределенные системы: опти- мизация и приложения в экономике и науках об окружающей среде, Ин-т матем. и механ. УрО РАН, Екатеринбург, 2000, 66–69

[10] Сумин М. И., “Регуляризованный градиентный двойственный метод решения об- ратной задачи финального наблюдения для параболического уравнения”, Ж. вы- числ. матем. и матем. физ., 44:11 (2004), 2001–2019 Math-Net.Ru MathSciNet MathSciNet Zentralblatt MATH

[11] Сумин М. И., “Регуляризация в линейно выпуклой задаче математического про- граммирования на основе теории двойственности”, Ж. вычисл. матем. и матем. физ., 47:4 (2007), 602–625 Math-Net.Ru MathSciNet MathSciNet Zentralblatt MATH

[12] Sumin M. I., “Parametric dual regularization in a linear-convex mathematical programming”, Comput. Optimizat. New Res. Developments, Ch. 10, Nova Sci. Publ. Inc., New–York, 2010, 265–311

[13] Варга Дж., Оптимальное управление дифференциальными и функциональными уравнениями, Наука, М., 1977 MathSciNet MathSciNet

[14] Сумин М. И., “Регуляризованный двойственный метод решения нелинейной за- дачи математического программирования”, Ж. вычисл. матем. и матем. физ., 47:5 (2007), 796–816 Math-Net.Ru MathSciNet MathSciNet Zentralblatt MATH

[15] Sumin M. I., “Parametric dual regularization in a nonlinear mathematical programming”, Ch. 5, Advances Math. Res., 11, Nova Sci. Publ. Inc., New–York, 2010, 103–134

[16] Borwein J. M., Strojwas H. M., “Proximal analysis and boundaries of closed sets in banach space. Part I: Theory”, Can. J. Math., 38:2 (1986), 431–452 crossref MathSciNet MathSciNet Zentralblatt MATH ; “Part II: Applications”, Can. J. Math., 39:2 (1987), 428–472 crossref Zentralblatt MATH

[17] Кларк Ф., Оптимизация и негладкий анализ, Наука, М., 1988 MathSciNet MathSciNet Zentralblatt MATH

[18] Loewen P. D., Optimal control via nonsmooth analysis, CRM Proc. Lecture Notes, 2, Amer. Math. Soc., Providence, RI, 1993 MathSciNet MathSciNet Zentralblatt MATH

[19] А. В. Канатов, М. И. Сумин Секвенциальная устойчивая теорема Куна–Таккера в нелинейном программировании Журнал вычислительной математики и математической физики, 2013, 53:8, 1249–1271.

ПРИЛОЖЕНИЕ