Формулировка и доказательство теоремы Куна-Таккера

Теорема Куна-Таккера является обобщением методов решения оптимизационных задач в двух направлениях:

- линейного программирования на нелинейный случай, который получил по аналогии не очень удачное название «нелинейного программирования»;

- нелинейных ограничений равенств на ограничения неравенства.

Метод и условия Каруша-Куна-Таккера (Karush-Kuhn- Tucker conditions, KKT) формально являются необходимыми условиями оптимальности задачи нелинейного программирования. Кроме того, необходимые условия включают, так называемые условия регулярности стационарных точек – невырожденность множества градиентов ограничений. Метод является обобщением метода множителей Лагранжа на случай ограничений неравенств.

Кун и Таккер обобщили метод множителей Лагранжа (для использования при построении критериев оптимальности для задач с ограничениями в виде равенств) на случай общей задачи нелинейного программирования с ограничениями, как в виде равенств, так и в виде неравенств .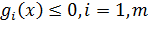

Основным методом в нелинейном программировании до сих пор остаётся применение функции Лагранжа, полученной переносом ограничений в целевую функцию. Условия Куна-Таккера также выведены из этого принципа.

Вильям Каруш в своей дипломной работе в 1931 году нашёл необходимые условия в общем случае ограничений равенств и неравенств. Независимо от него к тем же выводам позднее в 1941 году пришли Гарольд Кун и Альберт Таккер. Полученные ими результаты были более общими.

Если 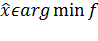при наложенных ограничениях является решением задачи, то найдётся вектор множителей Лагранжа 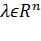такой, что для функции Лагранжа 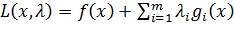выполняются условия:

- стационарности: ;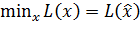

- дополняющей нежёсткости: ;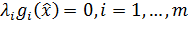

- неотрицательности:.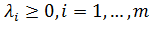

Перечисленные необходимые условия минимума функции в общем случае не являются достаточными. Существует несколько вариантов дополнительных условий, которые делают их достаточными:

- простое условие – 1) точка 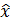стационарна, 2)выполняется условие дополняющей нежесткости, 3) множители Лагранжа ;

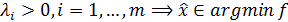- условие Слейтера(более слабое) – 1) точка 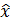стационарна, 2) выполняется условие дополняющей нежесткости, 3) .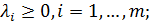

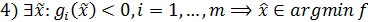Перейдём непосредственно к доказательству теоремы Куна-Таккера.

Если непрерывная функция n переменных x = (x1,...,xn) F(х) имеет в точкех_оптмаксимум, то существует ε > 0 такое, что для всех xиз ε-окрестности точких_опт

F(x)≤F(x_опт)

или

F(x)-F(x_опт)≤0.

Выберем два вида приращения x_j вдоль j-й координаты

Δx_j=x_j-x_jопт>0,

Δx_j=x_j-x_jопт<0.

Тогда

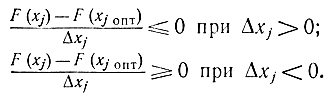
Переходя в этих соотношениях к пределу при Δx_j→0, получаем:

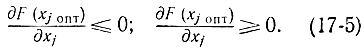
Из этих соотношений следует, что

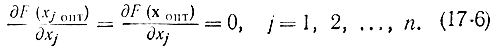(3.6.1)

Аналогичное соотношение можно получить для случая минимума функции. Таким образом, доказана необходимость условий (3.6.1) для достижения в точке х_опт максимума или минимума функции f(х), т. е. если имеется экстремум, то условия (3.6.1) удовлетворяются. Но равенство нулю всех производных в точке х_опт еще не обеспечивает существования в ней экстремума, т. е. условия (3.6.1) не являются достаточными. Геометрически это означает, что в случае нулевой производной от функции одной переменной может иметь место точка перегиба, а не максимум (или минимум), а в случае функции двух переменных - седловая точка, а не экстремум и т. д. Поэтому точки х_опт, в которых выполняются соотношения (3.6.1), называются стационарными.

Заметим, что условие (3.6.1) удалось получить благодаря возможности придавать переменной х приращения двух знаков, откуда и возникли два неравенства 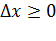при и при 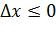. Если допустимая область значений х ограничена неотрицательными значениями х≥0, то внутри области, где х > 0, справедливость условия (3.6.1) сохраняется, так как там допустимы приращения обоих знаков. На границе области х ≥ 0, где х = 0, допускается только положительное приращение Δх >0, можно говорить только об односторонней производной, и из (3.6.1) следует следующее необходимое условие максимума:

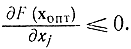
Соответственно, необходимое условие минимума на границе области х_j = 0 запишется в виде

.

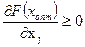б) Задача на условный экстремум

При определении условного экстремума функции, когда требуется определить максимум (или минимум) функции F(х) при ограничивающих условиях:

g_i(x) = b_i, i = 1, ..., m,

т. е.

f(x)=max;

g_i(x)=b_i;

используется также метод множителей Лагранжа, который, так же как в случае классического вариационного исчисления, заключается во введении функции Лагранжа

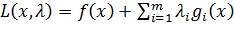(3.6.2)

где λ_i - неопределенные множители Лагранжа.

Полагая, что функция является частным случаем функционала, получаем, что необходимые условия экстремума находятся прямым дифференцированием соотношения (3.6.2) и записываются в виде

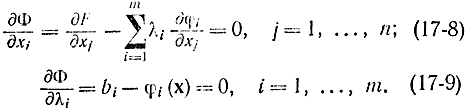
Если ввести в рассмотрение векторы

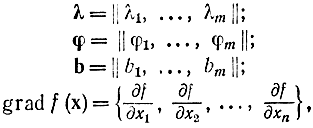
соотношения (17-8) и (17-9) перепишутся как

grad Φ = grad F - λ grad φ = 0; (3.6.6)

b - φ = 0,

где равенство нулю векторов понимается покомпонентно.

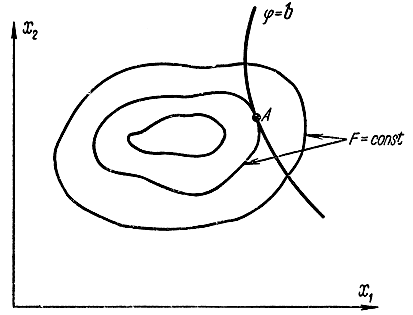
Рисунок 3.6.1 - Пояснение к задаче на условный экстремум

В случае n = 2 и m = 1 геометрическая задача об отыскании условного экстремума сводится (рис. 17-6) к отысканию точки касания А кривой φ = b к одной из кривых постоянного уровня f = const.