Классификация методов программирования

ААААААААААА

2.2 Необходимые и достаточные условия безусловного экстремума (§ 20)

Дадим общее определение задачи поиска экстремума и основные положения. Безусловного и условного.

Градиент и матрица Гессе 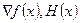. Положительная определённость.

Выпуклые множества и функции. Условие Липшица.

Постановка задачи. Рассматриваются функции 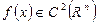– дважды непрерывно дифференцируемые.

Стратегия решения задачи состоит в нахождении точек 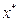локальных экстремумов и вычисления значений функции 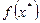в этих точках с помощью следующих средств:

- необходимых условий первого и второго порядка (порядок используемых производных);

- достаточных условий.

Необходимые условия (1-го порядка): 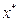– точка локального минимума (максимума), 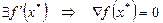. Это стационарная точка.

Необходимые условия (2-го порядка): 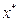– точка локального минимума (максимума), .

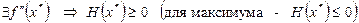Достаточные условия: 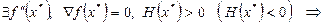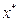– точка локального минимума (максимума).

Определитель матрицы Гессе, угловые миноры, главные миноры.

Для проверки определённости знака матрицы Гессе 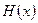обычно используют 2 способа:

1. А) Критерий Сильвестра (с помощью угловых 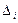и главных 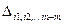миноров) – проверка достаточных (и необходимых) условий экстремума:

.

.

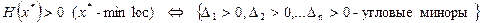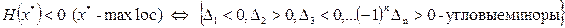Б) Критерий проверки необходимых условий 2-го порядка:

.

.

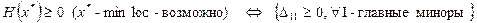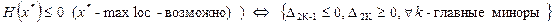2. Способ «по собственным значениям матрицы Гессе»:

.

.

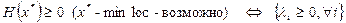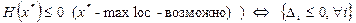Для скалярной функции (одной переменной) имеется более определённый критерий необходимости и достаточности.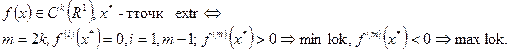

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ

- Найти стационарные точки, т.е. .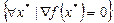

- Найти матрицу Гессе во всех стационарных точках .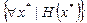

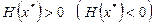- – локальный минимум (максимум) (проверка через угловые миноры или собственные числа);

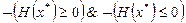- – нет экстремума (проверка через главные миноры или собственные числа);

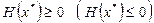- – возможен локальный минимум (максимум), требуется дальнейшее исследование, обычно, на основе разложения в ряд Тейлора (проверка через главные миноры или собственные числа);

Глобальные экстремумы находятся сравнением локальных. Строго выпуклые функции имеют ровно 1 минимум.

ЗАНЯТИЕ № 2 – 14 февраля 2013.

1.3 «Необходимые и достаточные условия условного экстремума».

1.3.1. Постановка задачи и основные определения. Пусть :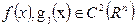

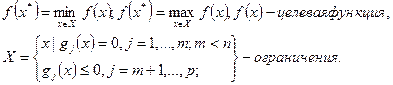
Основным методом решения таких задач является «Метод множителей Лагранжа».

Функцией Лагранжа называется

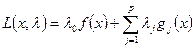– обобщённая функция Лагранжа.

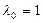– классическая функция Лагранжа.

Далее теория использует функцию Лагранжа в качестве целевой функции с параметрами 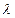(которые необходимо также определить):

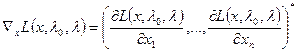– градиент функции Лагранжа (классической или обобщённой).

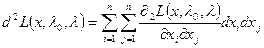– второй дифференциал функции Лагранжа (классической или обобщённой).

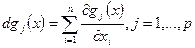– первый дифференциал ограничения.

Ограничение 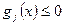называется активным в точке 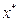, если 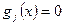(иначе – пассивным).

Различают линейно независимые или линейно зависимые в точке 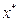градиенты ограничений: 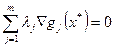. При линейной зависимости точку 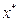называют «регулярной».

1.3.3. Условный экстремум типа равенств

Стратегия решения аналогична решению задачи без ограничений, но требует для определения точек экстремума 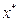нахождения значений m линейно независимых параметров из m+1 параметра 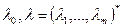– для чего имеется дополнительно необходимых m уравнений.

Проверяемые условия делятся (аналогично случаю безусловного экстремума) на необходимые и достаточные:

Необходимые условия 1-го порядка:

- стационарность ;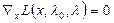

- допустимость ;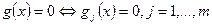

- регулярность 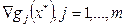, т.е. линейная независимость ( ).

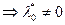Условия стационарности и допустимости образуют систему n+m уравнений с n+m+1 неизвестными. Её решения называются условно-стационарными точками.

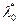Как избавиться от одного лишнего неизвестного? Если точка регулярная, т.е. ( – нерегулярная точка), то на это и делят уравнение для градиента и получают необходимое. Если про регулярность неизвестно (проверка затруднена), то просто рассматривают два случая: 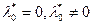, и тоже всё нормально.

В регулярной точке, имеем уравнение без 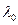, т.е.классическое, тогда

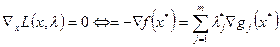– т.е. антиградиент целевой функции равен линейной комбинации градиентов ограничений.

Отсюда виден физический смысл этих векторов и коэффициентов 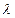. Точка экстремума 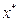является точкой касания линии уровня целевой функции и кривой, описывающей ограничение. Если точка не является точкой касания, то всегда можно пройти по градиенту вдоль ограничения с увеличением функции (по антиградиенту с уменьшением функции).

Для нерегулярной точки в функции Лагранжа исчезает член с целевой функцией и ограничения становятся линейно зависимыми, т.е. вырожденными. Тогда, надо избавиться от лишних ограничений, оставив максимальное линейно независимое их множество.

Необходимые условия 2-го порядка:

- пусть выполнены необходимые условия 1-го порядка, т.е. 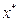– регулярная точка и найдено решение 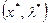системы уравнений , ;

-

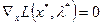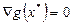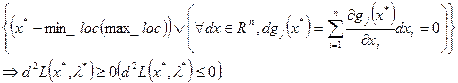
Достаточные условия 2-го порядка:

- пусть 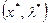– решение системы уравнений , ;

-

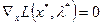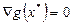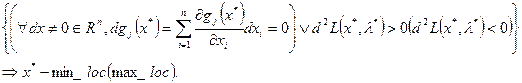
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ

- Составить обобщённую функцию Лагранжа .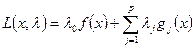

- Составить систему уравнений , .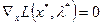

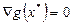- Решить систему, т.е. найти условно стационарные точки для двух случаев: 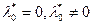. Если удаётся проверить условие линейной независимости градиентов ограничений 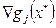, то отсутствует случай .

- Записать выражение для 2-го дифференциала классической функции Лагранжа в точке : .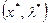

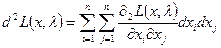- Записать систему уравнений для дифференциалов ограничений: .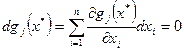

Из предыдущей системы выразить любые m дифференциалов 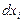через остальные n-m и подставить в :

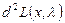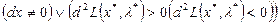- – локальный минимум (максимум);

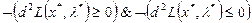- – нет экстремума;

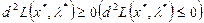- – возможен локальный минимум (максимум), требуется дальнейшее исследование, обычно, на основе разложения в ряд Тейлора и нахождения следующих дифференциалов.

Глобальные экстремумы находятся сравнением локальных. Строго выпуклые функции имеют ровно 1 минимум.

ЗАДАЧИ. № 3.5, ….

ЗАНЯТИЕ №3-4 – 14, 21 февраля 2013.

1.3.4. Условный экстремум типа неравенств

1. Постановка задачи и основные определения. Пусть :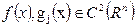

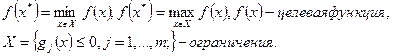
Проверяемые условия делятся (аналогично случаям безусловного экстремума и ограничениям типа равенства) на необходимые и достаточные:

Необходимые условия 1-го порядка:

- стационарность ;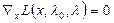

- допустимость ;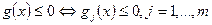

- неотрицательность для минимума 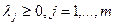(неположительность для максимума );

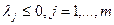- дополняющая нежёсткость ;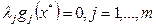

- регулярность 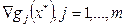, т.е. линейная независимость ( ).

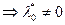Уже из этих условий видно, что решение задачи с ограничениями типа неравенств обладает рядом существенных, усложняющих отличий, главным из которых является условие дополняющей нежесткости 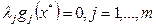с дополнительным условием одинаковости знаков всех коэффициентов 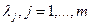. Определим 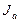– множество индексов ограничений, активных в точке 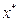, т.е. в которых неравенства реализуются равенствами: 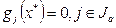, т.е. – положением точки на границе данного ограничения. Таким образом, если ограничение неактивно 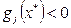, то соответствующее ему 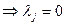. Это соотношение является ключом к решению задачи.

Заметим ещё, что для выпуклых функций приведённые необходимые условия являются и достаточными, а множество допустимых решений – выпукло.

Достаточные условия минимума (максимума) 1-го порядка:

- пусть точка 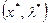– регулярная, т.е. ;

- ;

- .

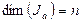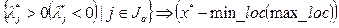Необходимые условия минимума (максимума) 2-го порядка:

- пусть выполнены необходимые условия 1-го порядка, т.е. 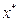– регулярная точка и найдено решение 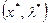системы уравнений для необходимых условий 1-го порядка;

-

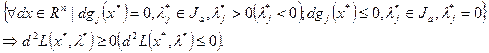
Достаточные условия минимума (максимума) 2-го порядка:

- пусть выполнены необходимые условия 1-го порядка, т.е. 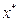– регулярная точка и найдено решение 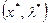системы уравнений для необходимых условий 1-го порядка;

- .

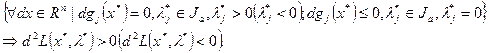АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ

- Составить обобщённую функцию Лагранжа .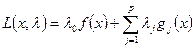

- Составить систему уравнений , , ( ), ;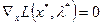

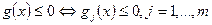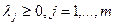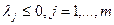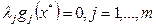- Решить систему, т.е. найти условно стационарные точки для двух случаев: 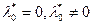. Если удаётся проверить условие линейной независимости градиентов ограничений 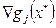, отсутствует случай ;

- Решение для обоих случаев делается для всех возможных 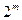комбинаций удовлетворения условий дополняющеё нежесткости;

- Определить число активных l ограничений в точке ;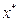

- ;

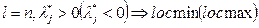- Если 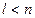, то работаем с дифференциалом 2-го порядка;

- Записать выражение для 2-го дифференциала классической функции Лагранжа в точке : .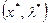

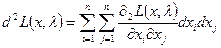- Записать систему уравнений для дифференциалов активных ограничений: .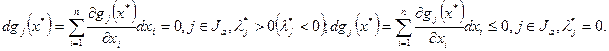

- Используя эти условия исследовать знак 2-го дифференциала :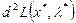

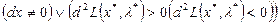- – локальный минимум (максимум);

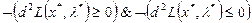- – нет экстремума;

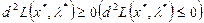- – возможен локальный минимум (максимум), требуется дальнейшее исследование, обычно, на основе разложения в ряд Тейлора и нахождения следующих дифференциалов.

Глобальные экстремумы находятся сравнением локальных. Строго выпуклые функции имеют ровно 1 минимум.

ПРИМЕР 3.12.

ЗАНЯТИЕ № 5 – 7 марта 2013.

1.3.4. Условный экстремум смешанного типа: равенства и неравенства

1. Постановка задачи и основные определения. Пусть :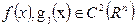

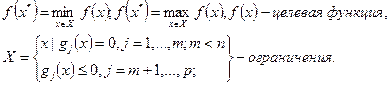
Исследование задачи получается простой комбинацией условий двух типов. Все формулировки аналогичны. Поэтому приведём только Алгоритм решения задачи.

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ

- Составить обобщённую функцию Лагранжа .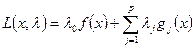

- Составить систему уравнений , , ;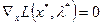

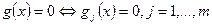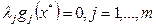- Решить систему, т.е. найти условно стационарные точки для двух случаев: 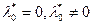, а также для всех возможных 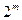комбинаций удовлетворения условий дополняющей нежесткости (если удаётся проверить условие линейной независимости градиентов ограничений 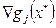, то отсутствует случай );

- Проверить выполнение ограничений неравенств в стационарных точках:

,

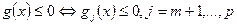- Определить число активных l ограничений 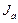в точке ;

- ;

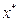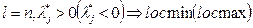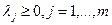
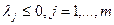- – может быть min, max.

- Если 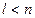, то работаем с дифференциалом 2-го порядка;

- Записать выражение для 2-го дифференциала классической функции Лагранжа в точке : .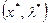

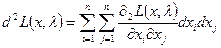- Записать систему уравнений и неравенств для дифференциалов активных ограничений: .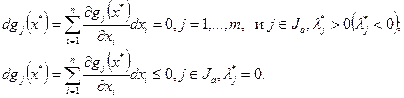

- Используя эти условия исследовать знак 2-го дифференциала :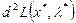

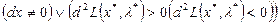- – локальный минимум (максимум);

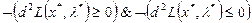- – нет экстремума;

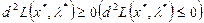– возможен локальный минимум (максимум), требуется дальнейшее исследование, обычно, на основе разложения в ряд Тейлора и нахождения дифференциалов более высокого порядка.

ЗАНЯТИЕ № 6 – 14 марта 2013.

Глава 2. Численные методы поиска безусловного экстремума

§4. Принципы построения численных методов поиска безусловного экстремума.

Аналитические методы не работают для подавляющего числа задач. Причинами являются: разрывность производных, сложностью решения получаемой системы нелинейных уравнений, неаналитическим или даже неявным заданием функции. Поэтому применяются численные методы.

Большинство численных методов являются итерационными: при заданной начальной точке 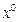пошагово генерируются точки последовательности 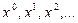, точнее 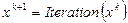, в которых значения функции сходятся к минимуму: .

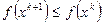Достаточно часто итерационная последовательность 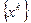строиться по формуле

,

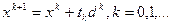где 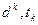– направление движения (спуска) и величина шага.

Для выполнения условия убывание функции 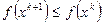необходимо

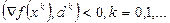
Отсюда видно, что большой класс образуют методы, где 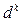определяется градиентом функции и его отдельными составляющими.

Величина шага часто определяется из условия

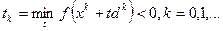
Сходящаяся к минимуму функции f последовательность называется «минимизирующей», а в случае сходимости 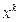, к точке 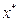, эта точка называется точкой минимума.

В зависимости от наибольшего порядка производных, используемых в методе, численные методы делятся на методы нулевого, первого и второго порядков.

§5.1. Методы нулевого порядка в одномерном случае.

5.1.1 Постановка задачи и стратегия поиска

Большинство методов предполагает нахождение аргумента в интервале и унимодальность (т.е. наличие единственного локального минимума на этом интервале) функции.

Замечания. 1) Непрерывная строго выпуклая функция – унимодальна, 2) Методы одномерной оптимизации широко используются при нахождении шага интерационного процесса.

Стратегия методов заключается в выборе итерационных точек. Она может быть пассивной, когда все точки заданы заранее, или активной, когда точки определяются в процессе функционирования метода.

Последовательная стратегия имеет следующие способы реализации:

1. Применение квадратичной и кубической интерполяции для выбранных точек и поиска минимума построенной интерполяционной кривой в качестве текущего приближения искомого минимума.

2. Построение последовательности вложенных друг в друга интервалов, содержащих точку минимума.

Стратегия состоит из трёх этапов:

1. Выбор начального интервала.

2. Построение последовательности интервалов, содержащих минимум.

3. Проверку условия окончания процесса поиска.

Алгоритм Свенна [Swann W.H.] определения начального интервала .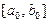

1. Задать произвольно следующие параметры: номер 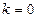, начальную точку 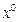, величину шага .

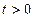2. Вычислить значения функции в трёх точках: .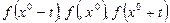

3. Проверить условие окончания:

- ;

- ;

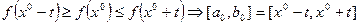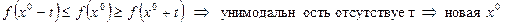- условие окончания не выполняется – перейти к шагу 4.

4. Определить величину :

- ;

- ;

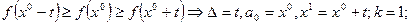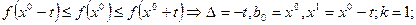5. Найти следующую точку .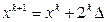

6. Проверить условие убывания функции:

- ;

- ;

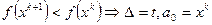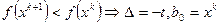- k=k+1 и перейти к шагу 5;

- .

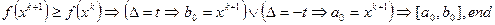При последовательной стратегии вычисляется функция в двух точках текущего интервала и на основании унимодальности отбрасывается левая или правая часть интервала.

5.1.2 Метод равномерного поиска

Задать 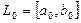– начальный интервал, N – число точек, где вычисляется функция f(x). Точки – равноотстоящие. Делаем: .

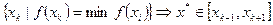5.1.3 Метод деления интервала пополам

Задать 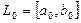– начальный интервал, l – требуемая точность, k=0. Вычислить точки .

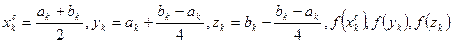Сравнить эти значения в трёх точках:

1. ;

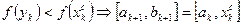2. ;

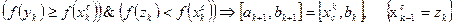3. .

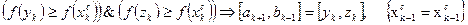5.1.4 Метод дихотомии

Идея метода состоит в разделении интервала области определения функции 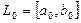на две равные части и сравнения значения функции в двух точках из разных половин. Выбираемые точки параметризуются величиной смещения от центра 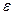, которую целесообразно для эффективности брать как можно меньше:

1. ,

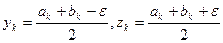2. ,

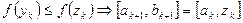3. ,

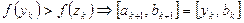5.1.5 Метод золотого сечения

Идея этого метода отличается от предыдущего только тем, что в качестве двух сравниваемых точек выбираются точки золотого сечения.

Определение. Золотое сечение отрезка 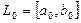точкой такое, что отношение всего отрезка к большей части равно отношению большей части к меньшей. Таких точек имеется две 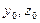, симметричные относительно середины отрезка:

. (*)

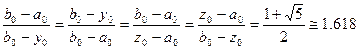Дополнительно точки 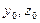производят золотые сечения отрезков 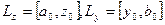, соответственно.

Последнее свойство приводит к необходимости вычисления согласно формуле (*) только одного нового значения функции на каждом шаге:

- ,

- ,

- .

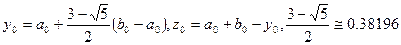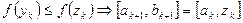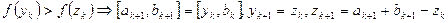5.1.6 Метод Фибоначчи

Идея этого метода аналогична методу золотого сечения и состоит в том, что из двух выбираемых точек одна остаётся такой точкой сравнения и для следующего интервала. Такая стратегия реализует максимальное гарантированное сокращение интервала при заданном количестве вычислений функции и претендует на оптимальность. Параметром метода является количество вычислений функции N. Точки вычисления функции находятся с использованием последовательности из N+1 числа Фибонччи.

Определение. Числа Фибоначчи определяются по формуле

.

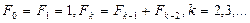Начальные конкретные значения: 1, 1, 2, 3, 5,8, 13, 21,34, 55, 89.

Алгоритм вычислений имеет вид:

1. найти количество вычислений N по формул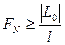е , где 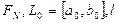– N-ое число Фибоначчи, начальный интервал, допустимая длина конечного интервала, соответственно,

2. ,

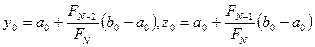3. ,

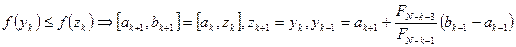4. .

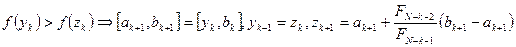5.1.7 Метод квадратичной интерполяции (Пауэлла [Powell M.J.D.])

Идея этого метода состоит в нахождении трёх точек как можно ближе к минимуму и дальнейшем построении квадратичного интерполяционного полинома, проходящего через эти точки. За точку минимума выбирается точка минимума квадратичного полинома:

1. параметры метода: начальная точка 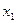, величина шага 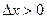, – характеристики точности,

2. ,

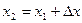3. ,

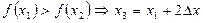4. ,

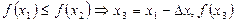5. найти ,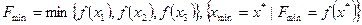

6. вычислить точку минимума и значение функции в этой точке: .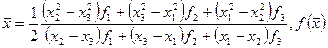

ЗАНЯТИЕ №7 – 21 марта 2013 – пропущено по болезни.

ЗАНЯТИЕ №8 – 28 марта 2013.

«Многомерный случай безусловных экстремумов. Методы нулевого порядка»

5.2 «Метод конфигураций (Хука-Дживса [R. Hook, T.A. Jeeves])».

Исследование ведётся от текущей базовой точки 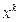вариациями сдвигов 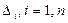, по координатам 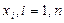в обе стороны (+ и –). В случае успешного результата делается движение по вектору, идущему из старой базовой точки 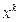в новую 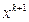. В случае успешного результата спуска по вектору – делается следующий аналогичный цикл. В случае неуспешного – возврат в старую точку 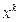и уменьшение параметров «координатных» 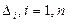и «векторных» 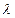сдвигов.

5.3 «Метод деформируемого многогранника (Нелдера-Мида [J.A. Nelder, R. Mead])».

В этом методе исследуемые на каждой итерации точки расположены в вершинах выпуклого многогранника. На каждой итерации выбрасывается наихудшая вершина и заменяется на новую вершину, выбранную специальным образом, на основе идеи движения в другую сторону от выброшенной точки. Многогранники в итоге стягиваются в точку-решение.

Параметрами метода являются:

1. координаты вершин многогранника 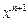, где n – размерность пространства координат;

2. 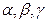– параметры отражения, сжатия, растяжения, соответственно;

3. 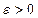– точность решения;

4. k – номер итерации.

5. Рекомендации по использованию параметров:

6. 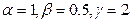– Нелдер и Мид;

7. 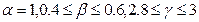– Павиани (D. Paviani);

8. 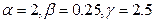– Паркинсон и Хатчисон [J.M. Parkinson, D. Hutchinson].

АЛГОРИТМ.

1. Задать параметры метода.

2. Найти «минимальную» (наилучшую) 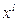и «максимальную» 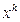и следующую по максимуму (наихудшие) 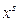вершины.

3. Найти центр тяжести всех вершин многогранника.

4. Проверить условие завершения – евклидова норма расстояний от вершин до центра < .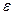

5. Операция отражения: наихудшей вершины через центр тяжести 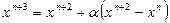и получить новый многогранник,

6. Проверить выполнение условий и сделать модификации вершин:

,

,

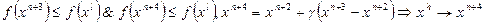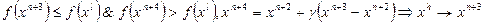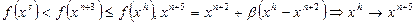– сжатие,

,

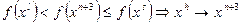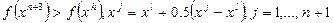– редукция.

5.4 «Метод Розенброка [H.H. Rosenbrok].

В этом методе осуществляется итеративный поиск направления убывания функции с помощью изменяемых дискретных шагов вдоль n векторов ортогонального базиса. Для удачного шага он увеличивается на следующей итерации, для неудачного – уменьшается, с помощью коэффициента. Если зашли в тупик, то строиться новый ортогональный базис. Новый базис поворачивается относительно старого вытегиванием вдоль «оврагов».

Параметрами метода являются:

1. начальная точка ;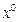

2. 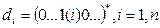– ортогональный базис;

3. 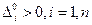– длины шагов для направлений поиска;

4. 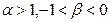– параметры растяжения, сжатия, соответственно;

5. 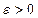– точность решения;

6. N – максимальное число неудачных серий шагов по всем направлениям на одной итерации.

АЛГОРИТМ.

1. Задать параметры метода.

2. 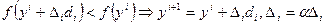– шаг по i-му направлению.

3.

Дэвис, Свенн и Кемпи [Davies D., Swann W.H., Campey I.G.] модифицировали метод Розенброка, применив метод одномерной оптимизации при поиске вдоль каждого направления .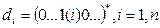

5.5 «Метод сопряжённых направлений (Пауэлла [M.J.D. Powell])»

5.6 «Методы случайного поиска (Нелдера-Мида [J.A. Nelder, R. Mead])»

ЗАНЯТИЕ №9 – 04 апреля 2013.

6. «Многомерный случай безусловных экстремумов. Методы первого порядка»

6.1 «Метод градиентного спуска с постоянным шагом».

Строиться последовательность точек 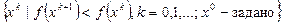по правилу 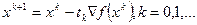Шаг 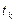– задаётся и остаётся постоянным, пока функция убывает. Иначе, например, делится попалам. Процесс оканчивается по условиям: 1) 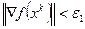или 2) 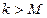– максимальное число итераций, или 3) 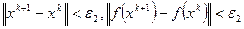– для двух последних шагов.

Параметры метода .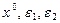

Для сильно выпуклой функции метод сходится к минимуму. Для Липцишевых функций метод сходится к стационарной точке.

Пример 6.1.

6.2 «Метод наискорейшего градиентного спуска».

От предыдущего метода с постоянным шагом отличается определением оптимального шага: 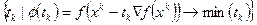. Последняя скалярная задача решается аналитическим или численными методами для скалярной задачи.

6.3 «Метод покоординатного спуска».

От предыдущих методов спуска по градиенту здесь на каждом цикле вычислений (состоящем из шагов по всем координатам) производиться спуск по всем отдельным частным производным: .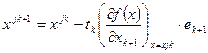

6.4 «Метод Гаусса-Зейделя [Gauss-Seidel]».

От предыдущего метода покоординатного спуска с постоянным шагом отличается определением оптимального шага: 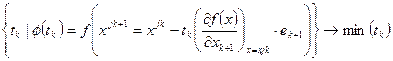, аналогично методу «наискорейшего градиентного спуска». Последняя скалярная задача решается аналитическим или численными методами для скалярной задачи.

6.5 «Метод Флетчера-Ривса [Fletcher R., Reeves C.M.]».

В этом методе итеративная последовательность точек строится по формуле: 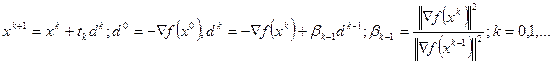. Шаг определяется из условия оптимальности .

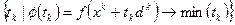Рассмотрим физический смысл этого метода. Пусть минимизируемая функция является квадратичной формой 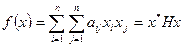, 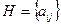. Тогда вычисление величины 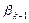обеспечивает построение последовательности H-сопряжённых направлений 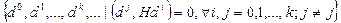. При этом в точках последовательности 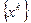последовательные пары градиентов функции 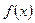взаимно ортогональны: 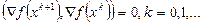. Для квадратичной функции 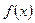и положительной матрицы H > 0 метод сходится не более, чем за n (размерность вектора x) шагов.

Для неквадратичных функций метод не является конечным, при этом нарушается ортогональность градиентов и H-сопряжённых направлений. В этом случае применяется модификация метода Полака-Рибьера [Polak E., Ribiere G.] с более сложным вычислением коэффициента 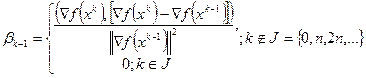. Кроме того, в отличие от метода Флетчера-Ривса метод Полака-Рибьера предусматривает использование итерации наискорейшего градиентного спуска после каждых n шагов.

6.6 «Метод Дэвидона-Флетчера-Пауэлла [Davidon W.C., Fletcher R., Powell M.J.D.]».

Это метод является обобщением метода наилучшего градиентного спуска, когда 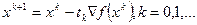и 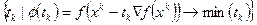. Вводится дополнительно 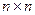матрица 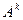: 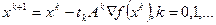и 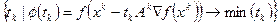, которая определяется по правилу: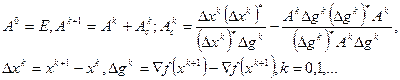

Рассмотрим физический смысл этого метода. Пусть минимизируемая

6.7 «Метод кубической интерполяции»

Находятся две такие точки, где производная имеет разные знаки. Вместе со значениями функции в этих двух точках получаем необходимые данные для построения кубического интерполяционного полинома (имеющего 4 параметра). И находиться его минимум.

ЗАДАЧИ.

7. «Многомерный случай безусловных экстремумов. Методы второго порядка»

7.1 «Метод Ньютона».

Этот классический метод второго порядка (т.е. использующий второй дифференциал функции) является основой для многих других, представляющих его модификации. Формула для вычисления итерационной последовательности имеет вид 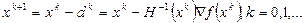Таким образом, вместо шага 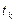например, в градиентном методе, используется боле сложное выражение – обратная матрица Гессе вторых частных производных 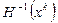. В этом случае, .

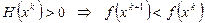Формула 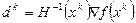получена из следующих соображений. Напишем разложение в ряд Тейлора в точке x с точностью до второго порядка функции 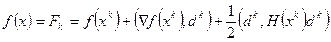. 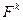– квадратичная форма. Направление (векто