Понятие функционального ряда и степенного ряда

Обычный числовой ряд, вспоминаем, состоит из чисел:

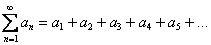
Все члены ряда 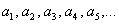– это ЧИСЛА.

Функциональный же ряд состоит из ФУНКЦИЙ:

В общий член ряда помимо многочленов, факториалов и других подарков непременно входит буковка «икс». Выглядит это, например, так: . Как и числовой ряд, любой функциональный ряд можно расписать в развернутом виде:

Все члены функционального ряда – это функции.

Наиболее популярной разновидностью функционального ряда является степенной ряд.

Определение: Степенной ряд – это ряд, в общий член которого входят целые положительные степени независимой переменной . Упрощенно степенной ряд во многих учебниках записывают так: , где – это старая знакомая «начинка» числовых рядов (многочлены, степени, факториалы, зависящие только от «эн»). Простейший пример:

Посмотрим на это разложение и еще раз осмыслим определение: члены степенного ряда содержат «иксы» в целых положительных (натуральных) степенях.

!!! Очень часто степенной ряд можно встретить в следующих «модификациях»: или , где – константа. Например:

Строго говоря, упрощенные записи степенного ряда , или не совсем корректны. В показателе степени вместо одинокой буквы «эн» может располагаться более сложное выражение, например:

Или такой степенной ряд:

Лишь бы показатели степеней при «иксАх» были натуральными.

Сходимость степенного ряда.
Интервал сходимости, радиус сходимости и область сходимости

!!! Не нужно пугаться такого обилия терминов, они идут «рядом друг с другом» и не представляют особых сложностей для понимания. Лучше выберем какой-нибудь простой ряд и начнём разбираться.

Степенной ряд .

Переменная может принимать любое действительное значение от «минус бесконечности» до «плюс бесконечности». Подставим в общий член ряда несколько произвольных значений «икс»:
Если , то
Если , то
Если , то
Если , то
И так далее.

!!! Очевидно, что, подставляя в то или иное значение «икс», мы получаем различные числовые ряды. Некоторые числовые ряды будут сходиться, а некоторые расходиться. И наша задача найти множество значений «икс», при котором степенной ряд будет сходиться. Такое множество и называется областью сходимости ряда.

Т.о., Определение: Областью сходимости ряданазывается совокупность тех значений х, при которых ряд сходится.

!!! Для любого степенного ряда (временно отвлекаемся от конкретного примера) возможны три случая:

1) Степенной ряд сходится абсолютно на некотором интервале . Иными словами, если мы выбираем любое значение «икс» из интервала и подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал и называется интервалом сходимости степенного ряда.

Радиус сходимости, если совсем просто, это половина длины интервала сходимости:

Определение:Число R– такое, что при ряд сходится, а при – ряд расходится, называется радиусом сходимости такого степенного ряда.

Определение:Радиус сходимости степенного ряда находится по формуле:

Геометрически ситуация выглядит так:

Широко распространен тривиальный случай, когда интервал сходимости симметричен относительно нуля:

>

Здесь интервал сходимости ряда: , радиус сходимости ряда:

Определение:Число R– такое, что при ряд сходится, а при – ряд расходится, называется радиусом сходимости такого степенного ряда.

Определение:Число R– такое, что при ряд сходится, а при – ряд расходится, называется радиусом сходимости такого степенного ряда.

В данном случае, интервал сходимости ряда: , радиус сходимости ряда:

!!! А что будет происходить на концах интервала ? В точках , степенной ряд может, как сходиться, так и расходится, и для выяснения этого необходимо проводить дополнительное исследование. После такого исследования речь идёт уже об области сходимости ряда:

– Если установлено, что степенной ряд расходится на обоих концах интервала, то область сходимости ряда совпадает с интервалом сходимости:

– Если установлено, что степенной ряд сходится на одном конце интервала и расходится на другом, то область сходимости рядапредставляет собой полуинтервал: или .

– Если установлено, что степенной ряд сходится на обоих концах интервала, то область сходимости ряда представляет собой отрезок:

!!! Термины очень похожи, область сходимости ряда – это чуть более детализированный интервал сходимости ряда.

С двумя оставшимися случаями всё короче и проще:

2) Степенной ряд сходится абсолютно при любом значении . То есть, какое бы значение «икс» мы не подставили в общий член степенного ряда – в любом случае у нас получится абсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают: . Радиус сходимости: .

3) Степенной ряд сходится в единственной точке. Если ряд имеет вид , то он будет сходиться в единственной точке . В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю: . Если ряд имеет вид , то он будет сходиться в единственной точке , если ряд имеет вид , то, понятно, – в точке «минус а». Радиус сходимости ряда во всех случаях, естественно, нулевой: .

!!! Других вариантов нет. Область сходимости степенного ряда – это всегда либо единственная точка, либо любое «икс», либо интервал (возможно полуинтервал, отрезок). Подчеркиваю, что данная классификация справедлива для степенных рядов. Для произвольного функционального ряда она в общем случае является неверной.