Интегральный признак Коши-Маклорена

Ряды

Числовые ряды

.1.1. Основные понятия

Пусть задана некоторая бесконечная последовательность чисел:

U₁, U₂, ... , U_n, ... (1).

Составленный их этих числе символ (формальное выражение)

U₁+U₂+ ... + U_n+ ... (2).

называется бесконечным чиловым рядом (или просто рядом). Вместо (2), пользуясь знаком суммы, часто пишут так:

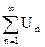(2а)

где символ å заменяет слово “сумма”, а индексы внизу и вверху означают, что нужно взять сумму чисел U_n, когда n пробегает все целочисленные значения от 1 до ¥. (Впрочем, нумерацию членов ряда иногда бывает удобнее начинать не с единицы, а с нуля или же с какого - либо натурального числа, большего единицы).

Числа U₁, U₂, ... , U_n, ... - называются членами ряда, а член ряда, стоящий на n-ом месте от начала - его общим членом.

Примеры рядов:

1-1+1-1+... ,

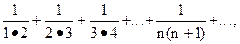
a+aq+aq²+...+aq^n-1+...

Задать ряд - это значит указать правило, закон образования его членов, по которому можно найти любой его член. Ряд можно задать формулой его общего члена. Например, если 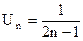, то тем самым определен следующий ряд:

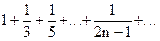
Выражение (2) является формальным, поскольку сумма бесконечного числа слагаемых не определена. Но поскольку в этом выражении между числами ряда знак суммирования, то подразумевается, что члены ряда как-то складываются. Сумма любого числа слагаемых будет найдена, если их складывать последовательно по одному. Это приводит к мысли поставить в соответствие ряду некоторое число и назвать его суммой ряда. С этой целью вводят понятие частичной суммы ряда.

Определение: Частичной суммой S_n числового ряда (2) называется сумма его первых n слагаемых, т.е.

S₁=U₁, S₂=U₁+U₂, S₃=U₁+U₂+U₃, ..., S_n=U₁+U₂+U₃+....+U_n.

Определение: Суммой числового ряда называется предел последовательности его частичных сумм, если этот предел существует

.

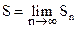Если 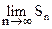cуществует, то ряд (2) называется сходящимся, если же 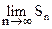не существует, то ряд (2) называется расходящимся. В частности, если 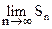=¥, то ряд расходится.

Примеры:

1. Рассмотрим ряд 1-1+1-1+1-... Найдем его частичные суммы S₁=1, S₂=0, S₃=1, S₄=0,... Последовательность его частичных сумм 1,0,1,0.1,0... не имеет предела, следовательно ряд расходится.

2. Рассмотрим ряд

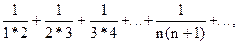
Найдем его частичные суммы:

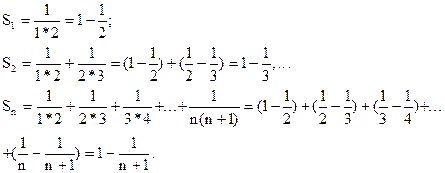
Так как 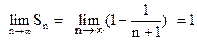, то рассматриваемый ряд сходится: его сумма равна 1.

3. Рассмотрим сумму членов геометрической прогрессии с первым членом а и знаменателем q (будем считать а¹0):

а+aq+aq²+aq³+...+aq^n-1+...

Известно, что сумма S_n первых прогрессии определяется по формуле

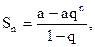или .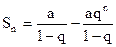

Рассмотрим несколько случаев в зависимости от величины q:

1. |q|<1. Тогда 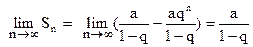(т.к. 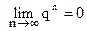). Следовательно, при |q|<1 ряд сходится и его сумма .

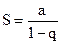2. |q|>1. Тогда |qⁿ|®¥ при n®¥, поэтому S_n®¥, т.е. 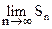не существует.

3. q=1. В этом случае ряд имеет вид а+а+а+...+а+...

При этом S_n=n*a и 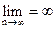, так как а¹0. Следовательно, ряд расходится.

4. q=-1. Тогда ряд имеет вид а-а+а-а+а-...(-1)^n-1а+... Его частичные суммы попеременно ранвы а и 0: S₁=a, S₂=0, S₃=a, S₄=0, ..., но такая последовательность не имеет предела, и, следовательно, рассматриваемый ряд расходится.

Итак, ряд составленный из членов геометрической прогрессии сходится тогда и только тогда, когда знаменатель прогрессии q по абсолютной величине меньше единицы.

1.2. Основные теоремы

Если в ряде (2) отбросить первые m членов, то получится ряд:

U_m+1+U_m+2+...+U_m+k+...= 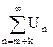(3)

называемый остатком ряда (2) после m-ого члена.

1^о. Если сходится ряд (2), то сходится и любой из его остатаков (3); обратно, их сходимости остатка (3) вытекает сходимость исходного ряда (2).

Фиксируем m и обозначим k-ю частичную сумму ряда (3) через S^|_k

S^|_k=U_m+1+U_m+2+...+U_m+k

Тогда, очевидно,

S^|_k= S_m+k - S_m (4).

Если ряд (2) сходится, так что S_n®S, то при неограниченном возрастании R -существует конечный предел

S^|= S - S_m (5)

и для суммы S^|_k , что и означает сходимость ряда (3). Обратно, если дано, что сходится ряд (3), так что S^|_k®S^|, то перепишем равенство (4), полагая в нем R=n-m (при n>m), так:

S_n=S_m+S^|_n-m

отсюда можно усмотреть, что при неограниченном возрастании n - частичная сумма S_n имеет предел

S=S_m+S^| (6),

т.е. сходится ряд (2).

Иными словами, отбрасывание конечного числа начальных членов ряда или присоединение вначале его нескольких новых членов не отражается на сходимости ряда.

Сумму ряда (3), если он сходится, обозначим вместо S^| символом a_m, указывая значком, после какого члена берется остаток. Тогда формулы (6) и (5) перепишутся следующим образом:

S=S_m+a_m, a_m=S-S_m.

Если увеличивать m до бесконечности, то S_m®S, а a_m®0. Итак:

2^о. Если ряд (2) сходится, то сумма a_m его остатка после m-ого члена с возрастанием m стремиться к нулю.

Упомянем следующие простые свойства сходящихся рядов:

3^о. Если члены сходящегося ряда (2) умножить на один и тот же множитель с, то его сходимость не нарушится (а сумма лишь умножится на с).

В самом деле, частичная сумм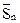а ряда

cU₁+cU₂+...+cU_n+...

очевидно, равна

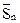= cU₁+cU₂+...+cU_n=c(U₁+U₂+...+U_n+=cS_n

и имеет пределом cА.

4^о. Два сходящихся ряда

А=а₁+а₂+...+a_n+... и

В=в₁+в₂+...+в_n+...

можно почленно складывать (или вычитать), так что ряд

(а₁±в₁)+(а₂±в₂)+...+(a_n±в_n)+...

также сходится, и его сумма равна, соответственно, А±В.

Если А_n, В_n и С_n означают частичные суммы упомянутых рядов, то, очевидно

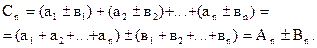
Переходя к пределу, найдем, что 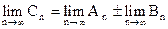, что и доказывает наше утверждение.

В заключение сделаем еще одно замечание.

5^o. Общий член U_n сходящегося ряда стремится к нулю. Это может быть доказанол совершенно элементарно: ряд S_n (а с ним и S_n-1)имеет конечный предел S, то

.

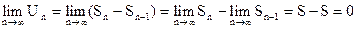Следствие. Если предел общего числа ряда при n®¥ не равен нулю, то ряд расходится.

Доказательство проведем отпротивного, т.е. допустим, что ряд сходится. Тогда в силу необходимого признака сходимости должно выполняться условие 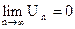. Но по условию предел общего члена ряда не равен нулю. Это противоречие означает, что предположение о сходимости ряда ошибочно; следовательно, ряд расходится.

Пример. Исследовать сходимость ряда

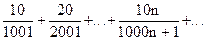
Найдем предел общего члена ряда при n®¥

.

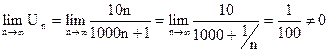Значит, данный ряд расходится.

Однако важно подчеркнуть, что необходимо условие сходимости ряда не является само по себе достаточным для сходимости ряда. Иными словами, даже при выполнении его ряд может расходится. Примером такого ряда служит ряд

,

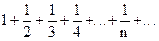который называется гармоническим. Последовательность его частичных сумм S₁=1, 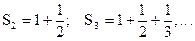монотонно возрастает, поскольку члены ряда положительны. Покажем, что она возрастает неограниченно. Для этого члены гармонического ряда, начиная с третьего, объединим в группы:

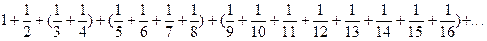
В первую включим два члена (3-й и 4-й), во вторую 2²=4 члена (с 5-го по 8-й), в третью 2³=8 членов (с 9-го по 16-й) и т.д., каждый раз увеличивая увеличивая вдвое число членов в группе. Таких групп, очевидно, бесконечное множество. Если заменить члены ряда в каждой группе их последними членами, то сумма членов этой группы уменьшится, т.е. справедливы неравенства

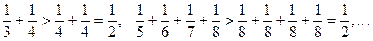
Таким образом, сумма членов каждой группы больше 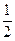, а сумма членов, включенных в достаточно большое число групп, как угодно велика. Следовательно, последовательность частичных сумм гармонического ряда неограниченно возрастает, а ряд расходится, хотя его общий член 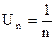при n®¥ стремится к нулю.

Заметим, что частичные суммы гармонического ряда возрастают, хотя и медленно. Например подсчитано, что S₁₀₀₀»7,48, а S_1000000»14,39.

1.3. Сходимость положительных рядов

Пусть ряд 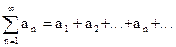будет положительным, т.е. a_n>0 (n=1,2,3,...).

Тогда очевидно, A_n+1=A_n+a_n+1>A_n, т.е. А_n оказывается возрастающей. На основании теоремы о пределе монотонной последовательности, мы непосредственно приходит к следующему основному в теории положительных рядов предложению!

Положительный ряд всегда имеет сумму; эта сумма будет конечной (и, следовательно, ряд - сходящимся), если частичные суммы ряда ограничены сверху, и бесконечной (а ряд - расходящимся) в противном случае.

1.4. Теоремы сравнения рядов

Сходимость или расходимость положительного ряда часто устанавливают путем сравнения его с другим рядом, заведомо сходящимся или расходящимся. В основе такого сравнения лежит следующая теорема.

Теорема 1. Пусть даны два положительных ряда

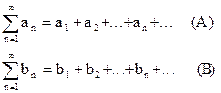
Если, хотя бы начиная с некоторого места (скажем, для n>N), выполняется неравенство: а_n£b_n, то из сходимости ряда (В) вытекает сходимость ряда (А) или - что то же - из расходимости ряда (А) следует расходимость ряда (В).

Доказательство. На основании того, что отбрасывание конечного числа начальных членов ряда не отражается на его поведении, мы можем считать, не нарушая общности, что а_n£b_n при всех значениях n=1,2,3,...

Обозначим частные суммы рядов (А) и (В), соответственно, через А_n и В_n, будем иметь: а_n£b_n.

Пусть ряд (В) сходится, тогда его частичные суммы В_n ограничены: В_n£L (L=const; n=1,2,3,...).

В силу предыдущего неравенства, и подобно А_n£L,а это, по той же теореме, влечет за собой сходимость ряда (А).

Иногда на практике более удобна следующая теорема, вытекающая из первой:

Теорема 2. Если существует предел (в предположении, что в_n¹0)

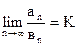(0£К£+¥)

то из схоимости ряда (В), при K<+¥, вытекает сходимость ряда (А), а из расходимости первого ряда, при K>0, вытекает расходимость второго. (Таким образом, при 0<К<+¥ оба ряда сходятся или оба расходятся одновременно).

Доказательство. Пусть ряд (В) сходится и К<+¥. Взяв произвольное число e>0, по самому определению предела, для достаточно больших n будем иметь

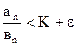, откуда а_n<(K+ e)в_n.

В силу 3^о одновременно с рядом (В) будет сходится и ряд å(К+e)в_n, полученный умножением его членов на постоянное число К+e. Отсюда, по предыдущей теореме, вытекает сходимость ряда (А).

Если же ряд (В) расходится и К>0, то в этом случае обратное отношение 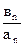имеет конечный предел; ряд (А) должен быть расходящимся, ибо если бы он сходился, то, по доказанному, сходился бы и ряд (В).

Примеры.

1. Исследовать сходимость ряда

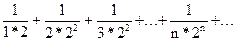
Члены ряда не превосходят соответствующих членов сходящегося ряда, составленного из членов геометрической прогрессии с общим числом :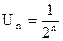

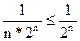(n=1,2,3,...).

Согласно теореме 1 данный ряд также сходится.

2. Ряд 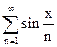(0<x<p) расходится по теореме 2; в силу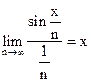

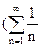- расходится).

Трудность применения на практике признаков (теорем 1 и 2) сравнения состоит в необходимости иметь “запас” рядов, сходимость (или расходимость) которых известна.

1.5. Признаки Даламбера и Коши

Теорема (признак Даламбера). Пусть для числового ряда с положительными членами:

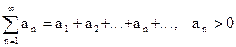
cуществует 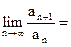l, то

при l<1 ряд сходится,

при l>1 ряд расходится,

при l=1 ряд может сходиться или расходиться (в этом случае признак на вопрос о сходимости ряда ответа не дает).

По определнию предела "e>0 $N=N(e), что "n>N выполняется неравенство:

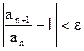или .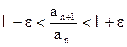

Выберем N так, чтобы для n>N было l+e=q<1, тогда

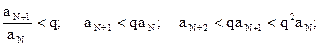
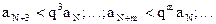
Ряд a_Nq+a_Nq²+...+a_Nq^m+... сходится, так как знаменатель прогрессии q<1. Тогда по теореме 1 ряд 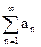также сходится.

Для случая q>1 доказательство аналогично, только нужно рассмотреть .

Пример. Исследовать на сходимость ряд

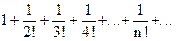
Решение. 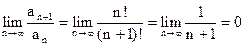- ряд сходится.

Рассмотрим ряд 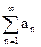с положительными членами a_n>0.

Признак Коши: Если существует 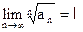, то при l<1 ряд сходится; l>1 - ряд расходится; l=1 — определить сходимость невозможно.

Доказательство признака Коши аналогично доказательству признака Даламбера.

Пример. Исследовать на сходимость ряд .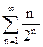

Применим признак Коши:

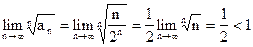- ряд сходится.

Теорема.

Пусть члены ряда удовлетворяют следующим условиям:

1) составляют монотонную невозрастающую последовательность

а₀ ³ а₁ ³ а₂ ³ а₃ ³ ... ³ а_n ³ ...;

2) можно построить монотонную невозрастающую функцию y = f(x) такую, что f(0) = a₀; f(1) = a₁; f(2) = a₂; ... ; f(n) = a_n; ... ;

3) несобственный интеграл 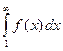- сходится, тогда заданный ряд также сходится. Если же интеграл расходится, то и ряд расходится.

Доказательство.

Составим частичную сумму S_n = a₀ + a₁ + a₂ + ... + a_n.

Поскольку a_i = f(i) ´ 1, то

S_n = f(0)´1 + f(1)´1 + f(2)´1 + ... + f(n)´1

S_n = f(0)´1 + f(1)´1 + f(2)´1 + ... + f(n)´1

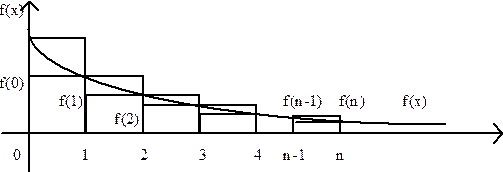
Рис. 1

Каждое слагаемое частичной суммы есть площадь прямоугольника с основанием единица и высотой, равной f(i) (Рис. 1). Добавление к частичной сумме нового члена ряда означает добавление новой площади, а потому S_n £ S_n+1, то есть последовательность частичных сумм неубывающая.

Рассмотрим частичную сумму S_n-1 = a₀ + a₁ + ... + a_n-1 и примем за a_i площадь прямоугольника, лежащего справа от f(i), т. е. с большей высотой. Тогда получим сумму площадей прямоугольников, часть площади которых расположена над кривой f(x). Эта площадь равна S_n-a_n. Рассмотрим сумму

а₁ + а₂ + ... + а_n = S_n - a₀.

Каждое слагаемое этой суммы есть площадь прямоугольника с основанием, равным единице, и маленькой высотой. Тогда сумма а₁ + а₂ + ... + а_n = S_n - a₀ есть сумма площадей прямоугольников, лежащих под кривой f(x). Рассмотрим

.

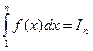С геометрической точки зрения этот интеграл есть площадь, ограниченная кривой f(x) при 0 £ x < n и осью Ох.

Тогда из рис. 1 имеем

S_n - a₀ £ J_n £ S_n - a_n Þ S_n £ J_n + a₀.

По условию теоремы существует предел

,

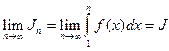тогда S_n £ J+a₀. Таким образом, последовательность {S_n} ограничена сверху, а потому имеет предел, значит ряд сходится.

Если 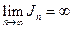, то учитывая, что S_n > J_n+a_n, откуда следует, что ряд расходится.

Доказанная теорема называется интегральным признаком Коши-Маклорена.

Пример

Исследовать на сходимость обощенный гармонический ряд .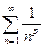

Решение. Члены ряда составляют монотонно убывающую последовательность .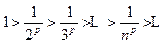

Следовательно, функцией f(x) будет .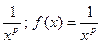

Рассмотрим 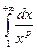и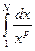

;

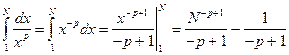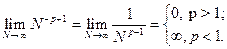
Тогда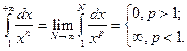

Если р=1, то имеем 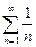- гармонический ряд, расходимость которого доказана ранее.

Ряд 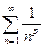сходится при р>1 и расходится при р £ 1.

Знакопеременные ряды

Прежде чем рассматривать ряды с членами произвольных знаков, расмотрим их частный случай, а именно ряды, члены которых имеют чередующиеся знаки, такие ряды называются знакочередующимися.

Знакочередующийся ряд, если первый член положителен, можно записать в виде:

U₁ - U₂ + U₃ - U₄ + ... + (-1)ⁿ⁺¹U_n + ... , где U_n>0, n=1, 2, 3, ...

Признак Лейбница

Если члены знакочередующегося ряда

U₁ - U₂ + U₃ - U₄ + ...

монотонно убывают по абсолютной величине, т. е.

U₁ ³ U₂ ³ U₃ ³ ... ³ U_n ³ U_n+1 ³ ...

и общий член ряда стремится к нулю, 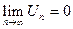, то:

1) ряд сходится;

2) его сумма не превосходит величины первого члена ряда

;

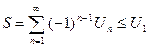3) модуль суммы остатка ряда не превосходит абсолютной величины первого отброшенного члена (первого члена остатка):

½r_n½ £ U_n+1; 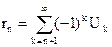и имеет знак своего первого члена.

Доказательство.

Построим S_2n = U₁ - U₂ + U₃ - U₄ + ... + U_2n-1 - U_2n = (U₁ - U₂) +

+ (U₃ - U₄) + ... + (U_2n-1 - U_2n).

Поскольку любая скобка в этой сумме больше нуля, то последовательность {S_2n} возрастающая. Докажем, что она ограниченная. Для этого представим S_2n следующим образом:

S_2n = U₁ - [(U₂ - U₃) + (U₄ - U₅) + ... + (U_2n-2 - U_2n-1) + U_2n].

Итак, последовательность {S_2n}монотонно возрастающая, ограниченная и, следовательно, сходящаяся. Пусть .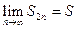

Чтобы доказать сходимость ряда, нужно доказать еще, что последовательность частичных сумм нечетного числа членов этого ряда также сходится и имеет предел, равный S.

Так как S_2n+1 = S_2n + U_2n+1 и U_2n+1 ® 0 (по условию), то

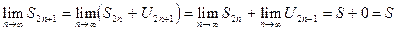
Заметим, что для суммы S ряда (1) справедливо соотношение 0<S<U₁. Действительно, частные суммы четных номеров S_2n, приближаются к сумме S, возрастая, следовательно, S>S_2n при любом n. Кроме того, S_2n>0 (n=1, 2, ...), а значит и S>0. Частные суммы нечетных номеров S_2n+1 можно записать в виде:

S_2n+1 = U₁ - (U₂ - U₃) - ... - (U_2n - U_2n+1).

Отсюда видно, что последовательность {S_2n+1} монотонно убывающая и что S_2n+1<U₁ при любом n. Так как S<S_2n+1 при любом n, то, следовательно, S<U₁. Суммируя сказанное, получаем: 0<S<U₁.

Рассмотрим теперь остаток ряда, умноженны й на (-1)ⁿ

(-1)ⁿ r _n= U_n+1 - U_n+2 + ...

Это ряд. По доказанному ряд сходится и его сумма не превосходит первого члена, то есть ½r_n½ < U_n+1.

Теорема доказана.

Пример

Ряд 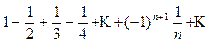сходится по признаку Лейбница. Этот ряд отличается от гармонического только знаками членов четных номеров.

Пример

Ряд 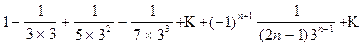cходится по признаку Лейбница:

.

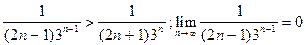Если положить его сумму S, приближенно равной сумме первых шести членов этого ряда, то получим ошибку, абсолютная величина которой меньше, чем

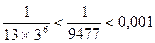, S » 0,907.

Теорема.

Если сходится ряд (8.2), то сходится и ряд (8.1).

Доказательство сразу получается из принципа сходимости : неравенство

|U_n+1 + U_n+2 + ... + U_n+m| £ |U_n+1| + |U_n+2| + ... + |U_n+m|

показывает, что если условие сходимости выполняется для ряда (8.2), то оно тем более выполняется для ряда (8.1).

Можно рассуждать иначе. Из положительных членов ряда (8.1), перенумеровав их по порядку, составим ряд

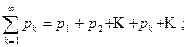(P),

так же поступим с отрицательными членами и составим ряд из их абсолютных величин

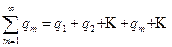(Q)

Сколько бы членов того или другого ряда ни взять, все они содержатся среди членов сходящегося ряда (8.2), и для всех частичных сумм Р_к и Q_m выполняется неравенства

Р_к £ S*; Q_m £ S*,

так что оба ряда (Р) и (Q) сходятся; обозначим их суммы соответсвенно, через Р и Q.

Если взять n членов ряда (А), то в их составе окажется k положительных и m отрицательных, так что

S_n = P_k - Q_m. (8.3)

Здесь номера k и m зависят от n. Если в ряде (8.1) как положительных, так и отрицательных членов бесчисленное множество, то при n®¥ одновременно k®¥ и m®¥.

Переходя в равенстве (8.3) к пределу, приходим снова к заключению о сходимости ряда (8.1), причем его сумма оказывается равной

S = P - Q.

Можно сказать, что при сделанных предположениях сумма данного ряда равна разности между суммой ряда, составленного из одних положительных его членов, и суммой ряда, составленного из абсолютных величин отрицательных членов.

Если ряд (8.1) сходится вместе с рядом (8.2), составленным из абсолютных величин его членов, то про ряд (8.1) говорят, что он абсолютно сходится.

Если ряд (8.1) сходится и ряд (8.2) расходится. Тогда ряд (8.1) называют условно сходящимся.

Между свойствами абсолютно и условно сходящихся рядов имеется глубокое различие.

Теорема.

Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов, причем сумма ряда не зависит от порядка его членов.

Если ряд сходится условно, то какое бы мы ни задали число А, или символ + ¥ или - ¥, можно так переставить члены этого ряда, чтобы его сумма оказалась в точности равной А (или + ¥ или - ¥). Более того, можно так переставить члены условно сходящегося ряда, что ряд, полученный после перестановки членов, окажется расходящимся.

На доказательство этой теоремы мы не будем останавливаться.

Приведем пример, показывающий, что сумма условно сходящегося ряда меняется при перестановке его членов.

Рассмотрим условно сходящийся ряд

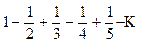(8.3)

Переставим его члены так, чтобы после одного положительного члена шло два отрицательных. Получим ряд

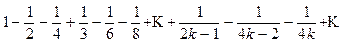(8.4)

Обозначим через S сумму данного ряда, покажем, что сумма полученного ряда равна 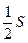. Обозначим через S_n и s_n частичные суммы рядов (8.3) и (8.4) и рассмотрим частичную сумму s_n при n = 3k.

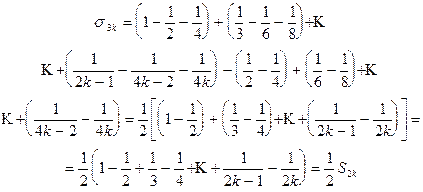
Следовательно, .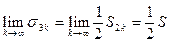

Далее замечаем, что

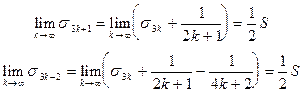
Таким образом, .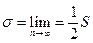

Итак, доказано, что в результате перестановки членов ряда его сумма изменилась (она вдвое уменьшилась).

Этот вывод, который на первый взгляд кажется парадоксальным, говорит о том, что бесконечные ряды отличаются по своим свойствам от сумм конечного числа слагаемых.

Теорема Абеля.

Если степенной ряд (9.1) сходится в точке х₀ ¹ 0, то он сходится и притом абсолютно в интервале (- |x₀|, |x₀| ), то есть при всех значениях х, удовлетворяющих условию |x|<|x₀|.

Следствие.

Если степенной ряд расходится при некотором значении х = х₁, то он расходится и при всех значениях |x|>|x₁|.

Любой степенной ряд сходится при значении х=0. Есть степенные ряды, которые сходятся только при х=0 и расходятся при остальных значениях х. Этот случай может быть иллюстрирован рядом

1 + х + 2² х² + ... + nⁿ xⁿ + ... ;

действительно, если х фиксировано и х ¹ 0, то начиная с достаточно большого n, будет |nx|>1, откуда вытекает неравенство |nⁿ xⁿ|>1, означающее, что общий член ряда не стремится к нулю.

Область сходимости может состоять из всех точек оси Ох, другими словами, ряд может сходится при всех х.

Пример.

Рассмотрим ряд .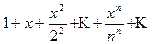

Для любого х, начиная с достаточно большого n, будет 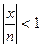. Так как 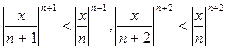и т. д., то, начиная с номера n, члены ряда по абсолютной величине будут меньше членов сходящейся геометрической прогрессии. Следовательно, при любом х ряд сходится.

Область сходимости ряда может состоять более чем из одной точки оси Ох, причем есть точки оси, не принадлежащие области сходимости.

Например, ряд 1 + х + х² + ... + хⁿ + ... , представляющий геометрическую прогрессию со знаменателем х, сходится при |x|<1 и расходится при |x|³1.

Из теоремы Абеля и ее следствия получаем, что все точки сходимости расположены от начала координат не дальше, чем любая из точек расходимости. Совершенно ясно, что точки сходимости будут целиком заполнять некоторый интервал с центром в начале координат.

Таким образом, можно сказать, что для каждого степенного ряда, имеющего как точки сходимости, так и точки расходимости, существует такое положительное число R, что для всех х, по модулю меньших R (|x|<R), ряд абсолютно сходится, а для всех х, по модулю больших R (|x|>R), ряд расходится.

Что касается значений х = R и х = - R, то здесь могут быть различные возможности: ряд может сходится в обеих точках, или только в одной из них, или ни в одной. При этом ряд может сходиться как абсолютно, так и условно.

Определение.

Радиусом сходимости степенного ряда (9.1) называется такое число R, что для всех х, |x|<R, степенной ряд сходится, а для всех х,|x|>R, расходится. Интервал (-R, R) называется интервалом сходимости.

Условимся для рядов, расходящихся при всех х, кроме х=0, считать R=0, а для рядов, сходящихся при всех х, считать R=¥.

Теорема.

Если все коэффициенты степенного ряда, начиная с некоторого, отличны от нуля, то его радиус сходимости равен пределу при n®¥ отношения абсолютных величин коэффициентов общего и следующего за ним членов ряда.

Доказательство.

Составим ряд из абсолютных величин членов ряда (9.1)

|c₀| + |c₁ x| + |c₂ x²| + ... + |c_n xⁿ| + ... (9.5)

Найдем отношение 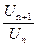для этого ряда:

,

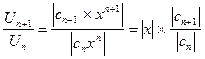а затем предел его при n®¥ :

.

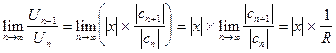Здесь множитель |x| вынесен за знак предела, как не зависящий от n, и введено обозначение

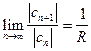, (9.6)

если этот предел существует и не равен нулю. Согласно признаку Даламбера, ряд (9.5) сходится, если 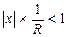, откуда |x|<R. Отсюда следует, что ряд (9.1) сходится, и притом абсолютно, при значениях |x|<R. Согласно тому же признаку Даламбера, ряд (9.5) расходится, если 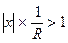, или |x|>R. Однако в этом случае из признака Даламбера следует, что члены ряда (9.5) не стремятся к нулю. Тогда при n®¥ не стремятся к нулю и члены ряда (9.1), а потому и он расходится при значениях |x|>R. Следовательно, согласно определению, число R - радиус сходимости степенного ряда (9.1). Из соотношения (9.6) получим

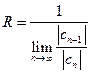, т. е. 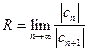. (9.7)

Приведем примеры:

1⁰ Найдем радиус сходимости ряда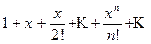

.

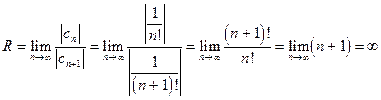2⁰ Найти область сходимости степенного ряда

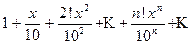
Найдем отношение

.

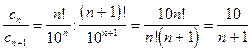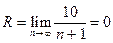, т. е. ряд сходится только при х=0 и расходится при остальных значениях х.

3⁰ Найти область сходимости степенного ряда:

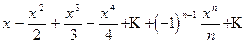
Здесь 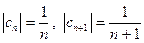, т. е.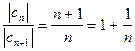

.

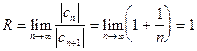Исследуем сходимость ряда на концах интервала сходимости.

При х=1 имеем ряд 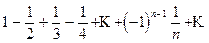, он сходится по теореме Лейбница.

При х=-1 имеем ряд 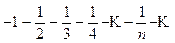, который расходится как произведение расходящегося гармонического ряда на -1. Следовательно, областью сходимости служит полуинтервал (-1; 1].

4⁰ Найти область сходимости степенного ряда

,

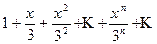Найдем радиус сходимости ряда

.

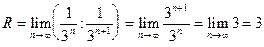Исследуем сходимость ряда при значениях х= ±3. Подставив их в в данный ряд соответственно получим 1 + 1 + 1 + ... + 1 + 1 + ... ;

1 - 1 + 1 - ... + (-1)ⁿ + ... . Оба ряда расходятся, так как не выполняется необходимое условие сходимости (их общие члены не стремятся к нулю при n®¥). На обоих концах интервала сходимости данный ряд расходится, а область его сходимости (-3; 3).

Формула радиуса сходимости степенного ряда получена в предположении, что все коэффиценты членов ряда, начиная с некоторого, отличны от нуля. Применение формулы (9.7) допустимо только в этих случаях. Если это условие нарушается, то радиус сходимости степенного ряда следует искать или с помощью признаков Даламбера, Коши, или же сделав замену переменной, преобразованием ряда к виду, в котором указанное условие выполняется.

Свойства степенных рядов

Рассмотрим степенной ряд

с₀ + с₁ х + с₂ х² + ... + с_{n xⁿ} + ... , (10.1)

имеющий радиус сходимости R>0 (R может равняться ¥). Тогда каждому значению х из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от х на интервале сходимости. Обозначим ее через S(x). Тогда можно записать равенство

S(x) = c₀ + c₁ x + c₂ x² + ... + c_n xⁿ + ... , (10.2)

понимая его в том смысле, что сумма ряда в каждой точке х из интервала сходимости равна значению функции S(x) в этой точке. В этом же смысле будем говорить, что ряд (10.1) сходится к функции S(x) на интервале сходимости. Вне интервала сходимости равенство (10.2) не имеет смысла.

Пример.

Найти сумму степенного ряда

1 - х + х² - ... + (-1)ⁿ xⁿ + ... .

Это ряд, составленный из членов геометрической прогрессии, у которой b₁=1, q= -x. Следовательно, его сумма есть функция 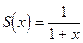. Ряд сходится, если |x|<1. Поэтому равенство

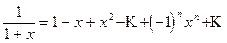
справедливо лишь для значений хÎ(-1; 1), хотя функция 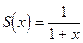определена для всех значений х, кроме х= -1.

Можно доказать, что сумма степенного ряда S(x) непрерывна и дифференцируема на любом отрезке [a, b] внутри интервала сходимости.

Равенство (10.2), справедливое в интервале сходимости степенного ряда, называют разложением S(x) в степенной ряд.

Для степенных рядов справедливы следующие утверждения:

Теорема 1.

Степенной ряд в интервале его сходимости можно почленно дифференцировать неограниченное число раз, причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны S`(x), S``(x), ... , S⁽ⁿ⁾(x).

Теорема 2.

Степенной ряд можно неограниченное число раз почленно интегрировать в пределах от 0 до х, если хÎ(-R; R), причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны .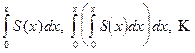

Примеры.

1. Разложить в ряд Маклорена функцию е^х.

Найдем производные (е^х)⁽ⁿ⁾ = e^x, поэтому при х=0 имеем
f(0) = f`(0) = ... = f⁽ⁿ⁾(0) = ... = 1. Подставляя эти значения в формулу (11.3) получим искомое разложение

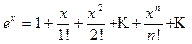(11.4)

Этот ряд сходится на всей числовой прямой R=¥.

2. Разложить в ряд Маклорена функцию f(x) = sin x.

f(x) = sin x, f`(x) = cos x, f``(x) = - sin x, f```(x) = -cos x, f^IV(x) = sin x.

Так как производная четвертого порядка совпадает с функцией, то производные следующих порядков повторяются в той же последовательности. Найдем значения функции и ее производных при х=0:

f(0)=0, f`(0)=1, f``(0)=0, f```(0)= -1, f^IV(0)=0, ... .

Поэтому ряд Маклорена для функции f(x) = sin x имеет вид

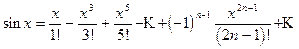(11.5)

Аналогично

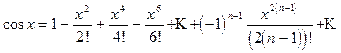
Можно доказать, что ряды (11.5) и (11.6) сходятся на всей числовой прямой.

Ряды

Числовые ряды

.1.1. Основные понятия

Пусть задана некоторая бесконечная последовательность чисел:

U₁, U₂, ... , U_n, ... (1).

Составленный их этих числе символ (формальное выражение)

U

Наши рекомендации