Теперь осуществим циклический групповой поиск.

Решение представлено в таблицах Excel

A	B	C	D	E
x1	x2	x3	x4	x5
x1+x2+x3+x4+x5<=30
x1<=4
x2<=3
x1+x2<=9
x3+x4<=3
fmin=
Начальные значения	x1=0	x2=0	x3=0
		x4=0	x5=0
группы
x1-x2
x3-x4
x5-x1
x2-x3
и т.д.

A	B	C	D	E
x1	x2	x3	x4	x5
x1+x2+x3+x4+x5<=30
x1<=4
x2<=3
x1+x2<=9
x3+x4<=3
fmin=
Начальные значения	x1=4	x2=3	x3=0
		x4=0	x5=0
группы
x1-x2
x3-x4
x5-x1
x2-x3
и т.д.

A	B	C	D	E
x1	x2	x3	x4	x5
x1+x2+x3+x4+x5<=30
x1<=4
x2<=3
x1+x2<=9
x3+x4<=3
fmin=
Начальные значения	x1=0	x2=3	x3=2
		x4=1	x5=0
группы
x1-x2
x3-x4
x5-x1
x2-x3
и т.д.

A	B	C	D	E
x1	x2	x3	x4	x5
x1+x2+x3+x4+x5<=30
x1<=4
x2<=3
x1+x2<=9
x3+x4<=3
fmin=
Начальные значения	x1=0	x2=0	x3=0
		x4=1	x5=0
группы
x1-x2
x3-x4
x5-x1
x2-x3
и т.д.

Улучшение решения по группам переменных завершено. В данном оно совпало с оптимальным решением. В общем случае требуется проверка решения путем изменения начальных условий.

Наличие точных математических моделей графических объектов позволяет относительно легко отображать их на экране монитора, а вычисленные матрицы преобразований дают возможность манипуляции этими объектами на экране и позволяют повысить наглядность визуального решения задач математического программирования.

«Нелинейная многокритериальная оптимизация»(АОИ)

Теоретическая часть.

Задача оптимизации управления рассматривается в общем случае как задача нелинейного программирования с несколькими целевыми функциями

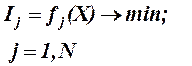(1)

при наличии линейных ограничений

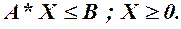(2)

Для простаты изложения результаты оптимизации сформулируем в терминах выпуклых функций (рис. 15 – Тема 5). Читатель без затруднений сможет получить аналогичные результаты для вогнутых функций. Если функция -выпукла, то «» вогнута.

Одним из наиболее важных свойств выпуклых функций является то ,что их неотрицательная линейная комбинация также выпукла.

Результаты вычислений представлены таблицей и диаграммами.

t	f1(t)	f2(t)	f3(t)	f1+2f2+5f3

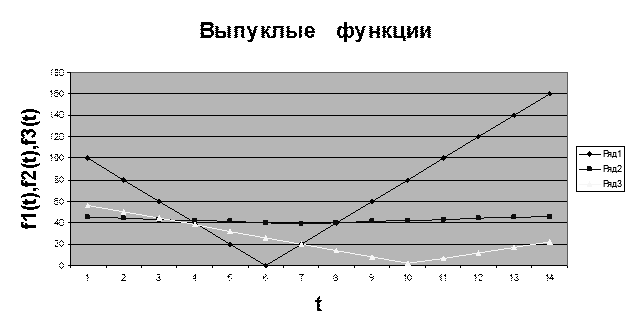
Рис. 1.

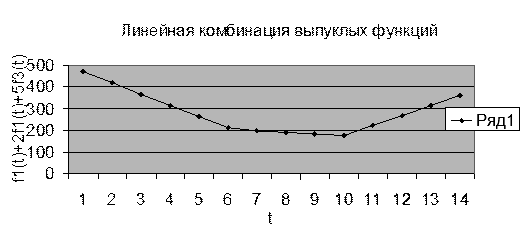
Рис. 2.

Выбором весов при суммировании выпуклых функций можно свести многокритериальную задачу к однокритериальной. При этом целесообразно предварительно исключить лишние неравенства. Математически строгое решение изложено в разделе по Теме 3.

С помощью многомерно-матричных представлений возможно упрощение точного численного метода решения системы линейных неравенств приближенным решением на основе графического построения области допустимых решений(ОДР) в MS Excel для большого числа ограничений и переменных. Множество условных символов (единиц) в многомерной матрице определяет ОДР. Для наглядности удобно произвести условное форматирование (Формат | Условное форматирование), изменив цвет единиц. Рассмотренный алгоритм позволяет при большом количестве ограничений получить ОДР и исключить лишние неравенства. Если при удалении неравенства 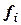область не изменяется, то данное неравенство 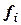является лишним и его можно удалить.

Определение согласованного вектора приоритетов различных критериев (МОИ)

Метод попарного сравнения.

Введем матрицу .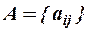

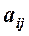- когда во сколько раз i-ый критерий важнее j-го

.

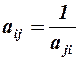Заполняем матрицу

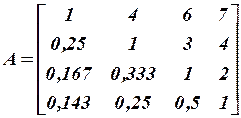
Находим самое большое собственное число и соответствующий ему собственный вектор

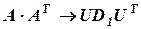- находим

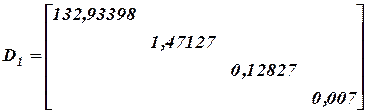
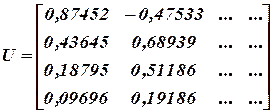
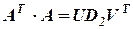
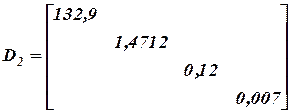
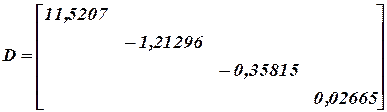
Самое большое собственное число 11,52. Все остальное обнуляем.

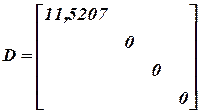
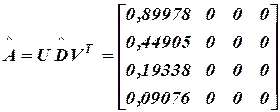
Нормализуем первый столбец матрицы

Вес 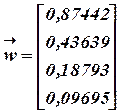- «согласованный» вектор весов

Введем погрешность 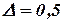. Вносим случайным образом в матрицу А

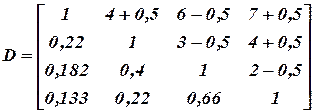
Сделаем для этой матрицы все то, что делали для исходной.

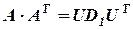
Находим 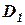и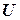

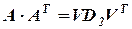
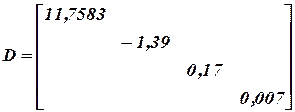
Далее обнуляем: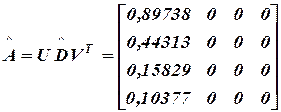

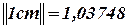
Делим каждый элемент на норму. Получаем:

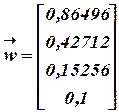
Вывод: согласованный вектор весов получается устойчивым. Он сформирован на основе 16-ти «измерений» (см. матрицу А). При увеличении матрицы А, число измерений растет, что обеспечивает устойчивость .