Передаточные функции соединений элементов
С переменными параметрами
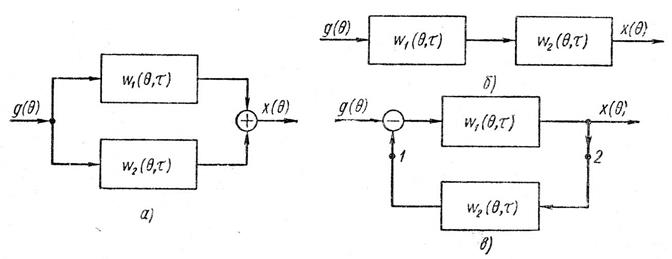
Соединения элементов с переменными параметрами:
а — параллельное; б — последовательное; в — с обратной связью
Параллельное соединение.
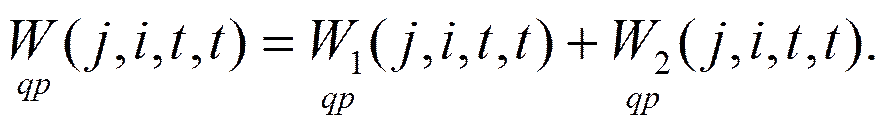
Последовательное соединение.
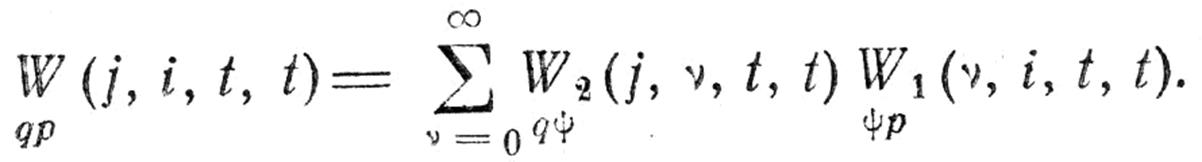(IV.63)
Соединение с обратной связью.
Матрица двумерной нестационарной передаточной функции замкнутой системы определяется формулой
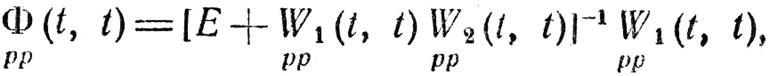
Можно найти другие формулы для матрицы двумерной нестационарной передаточной функции замкнутой системы, эквивалентные формуле
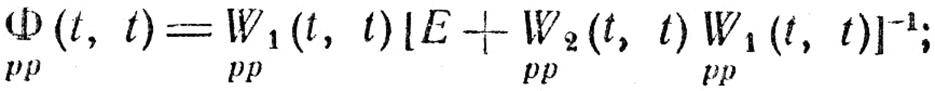
Связь нестационарных передаточных функций с дифференциальными уравнениями систем с переменными параметрами
Пусть система описывается дифференциальным уравнением с переменными коэффициентами
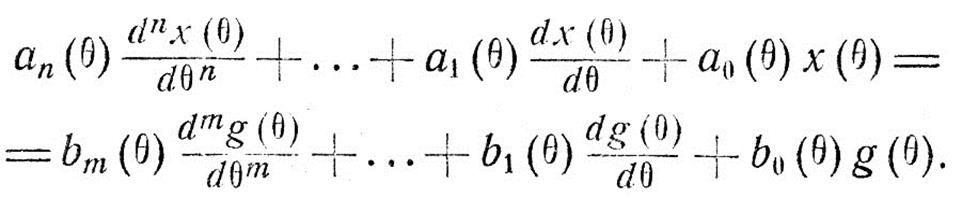(IV.80)
Импульсная переходная функция системы k(θ, τ) как функция θ является решением этого уравнения при воздействии g(θ) = δ(θ - τ):
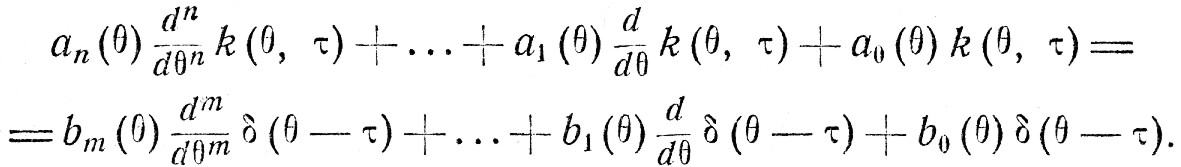(IV.81)
Умножим правую и левую части уравнения (IV.81) на функцию ψ(i, t, τ), которая принадлежит системе функций, ортонормированной на отрезке t - Т(t) ≤ τ ≤ t, и проинтегрируем обе части по τ на этом отрезке:
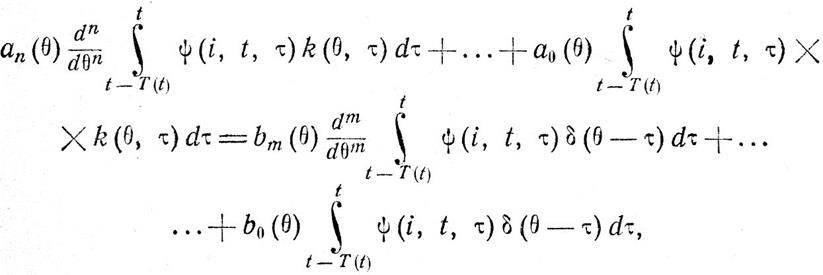
откуда, учитывая свойства дельта - функции, найдем:
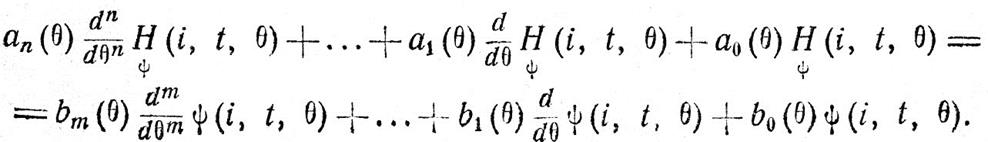
В уравнении i и t — параметры и всегда ψ(i, t, θ) = 0 при θ = t – T(t) – ε.
Заметим, что нестационарная сопряженная передаточная функция
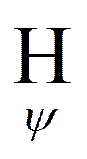(i, t, θ) является решением дифференциального уравнения системы при g(θ) = ψ(i, t, θ). Установим теперь связь двумерной нестационарной передаточной функции с дифференциальным уравнением системы.
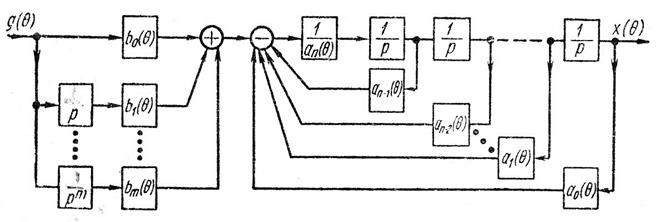
Структурная схема математической модели системы, построенная по дифференциальному уравнению
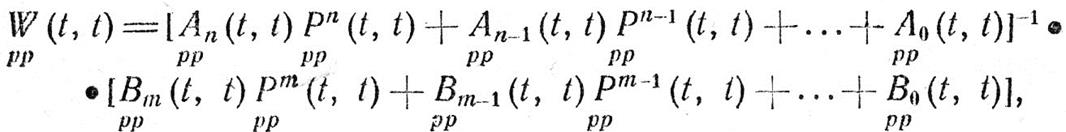
где P(t, t), A(t, t), B(t, t) — матрицы двумерных нестационарных передаточных функций соответственно дифференциатора и усилительных звеньев с импульсными переходными функциями ak(θ)δ(θ – τ), bk(θ)δ(θ – τ) определяемыми коэффициентами дифференциального уравнения.
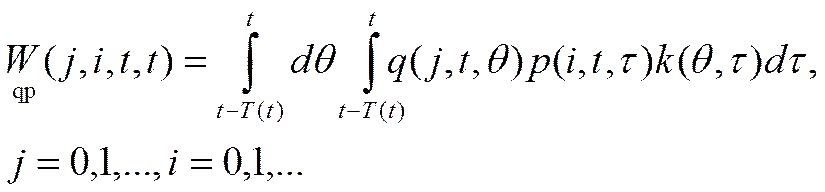
При выводе формулы учитывается, что матрицы двумерных нестационарных передаточных функций интегратора и дифференциатора обратны друг другу: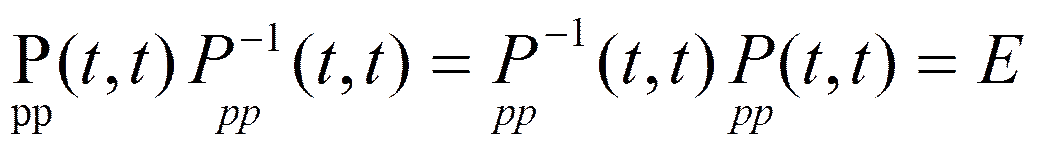 
, а матрицы двумерной нестационарной передаточной функции интегратора и дифференциатора порядка к определяются как степени матриц Р-1(t, t) и P(t, t).
Формулу можно представить также в форме, удобной при вычислениях:
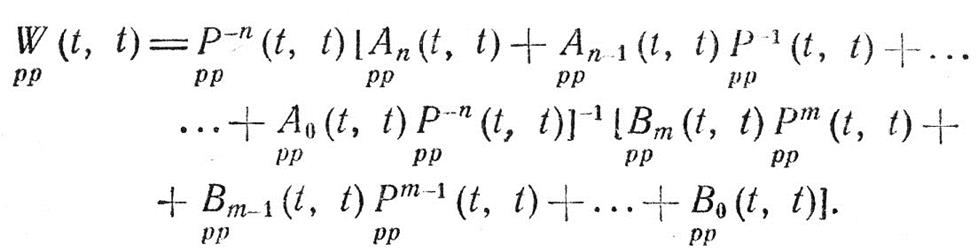
Если коэффициенты дифференциального уравнения постоянны, то формулы принимают вид
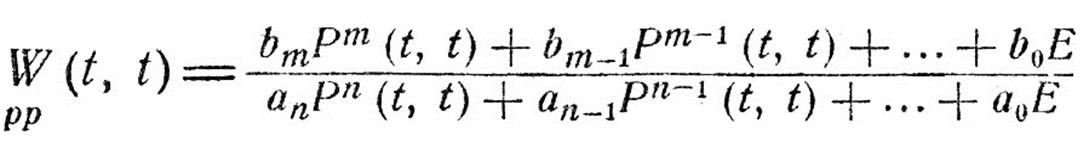(IV.85)
или
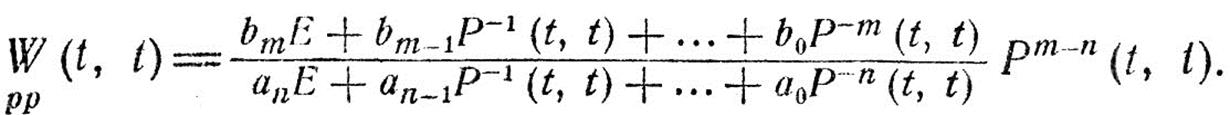
(IV.86)
Запись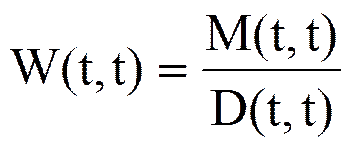 
в данном случае указывает, что для стационарной системы матрицы М и D-1 коммутативны.
Матрица двумерной передаточной функции {dne}дифференцирующего звена Р имеет вид
| … | … | … | … | … | … | … | … | … | … | … | … | … | ||
| … | d-4,-4 | … | d-4,-3 | d-4,-2 | d-4,-1 | d-4,0 | d-4,1 | d-4,2 | d-4,3 | … | d-4,n | … | -n | |
| … | … | … | … | … | … | … | … | … | … | … | … | … | ||
| … | d-3,-4 | … | 2-j6p | … | d-3,n | … | -3 | |||||||
| … | d-2,4 | … | 2-j4p | … | d-2,n | … | -2 | |||||||
| … | d-1,4 | … | 2-j2p | … | d-1,n | … | -1 | |||||||
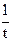 | … | d0,-n | … | … | d0,n | … | n=0 | |||||||
| … | d1,-4 | … | 2+j2p | … | d1,n | … | +1 | |||||||
| … | d2,-4 | … | 2+j4p | … | d2,n | … | +2 | |||||||
| … | d3,-4 | … | 2+j6p | … | d3,n | … | +3 | |||||||
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | |
| dn,-4 | … | dn,-3 | dn,-2 | dn,-1 | dn,0 | dn,1 | dn,2 | dn,3 | … | d-n,n | … | n | ||
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | |
| -n | -3 | -2 | -1 | e=0 | ... | n |
где dn,n=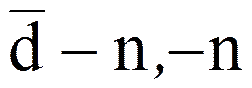 
=2+j2pn.
Спектральные характеристики, определенные относительно системы функции (2.2), представлены таблицей
| x(t) | 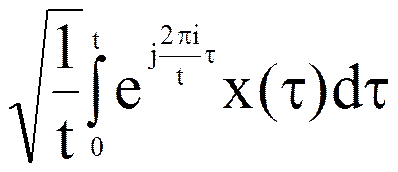 | i=0, ±1, ±2…. |
| 1(t) | 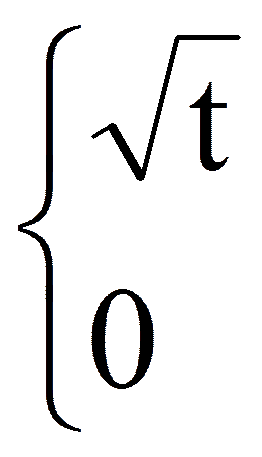 | i=0 i= ±1, ±2,… |
| t | 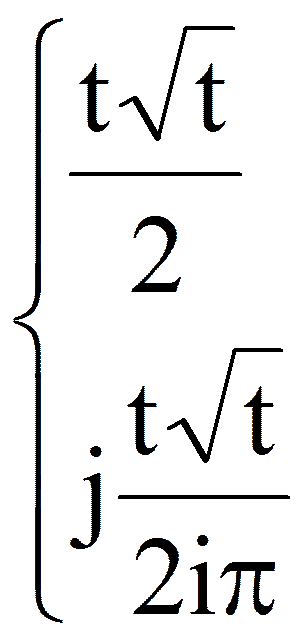 | i=0 i= ±1, ±2,… |
| t2 | 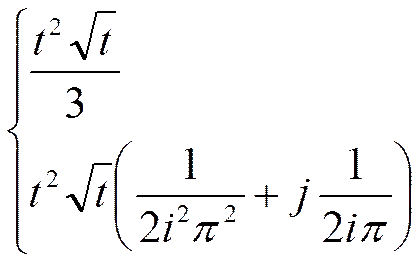 | i=0 i= ±1, ±2,… |
Матрица {dne} для линейного стационарного звена имеет вид
.
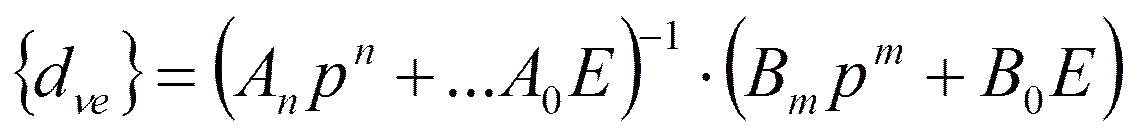Точность метода необходимо контролировать путем увеличения размерности матрицы Р.
******************************************
Пример.
При помощи троек однородных координат и матриц третьего порядка можно описать любое аффинное преобразование плоскости.
.
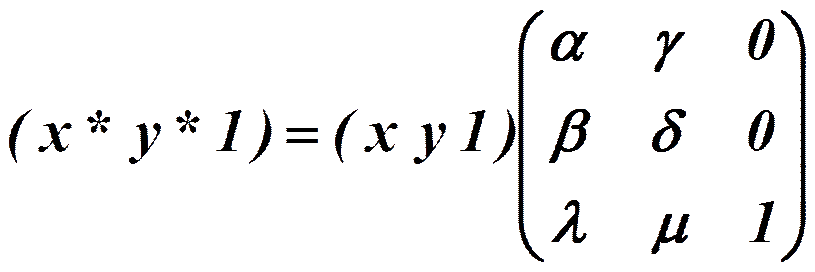А. Матрица вращения
.
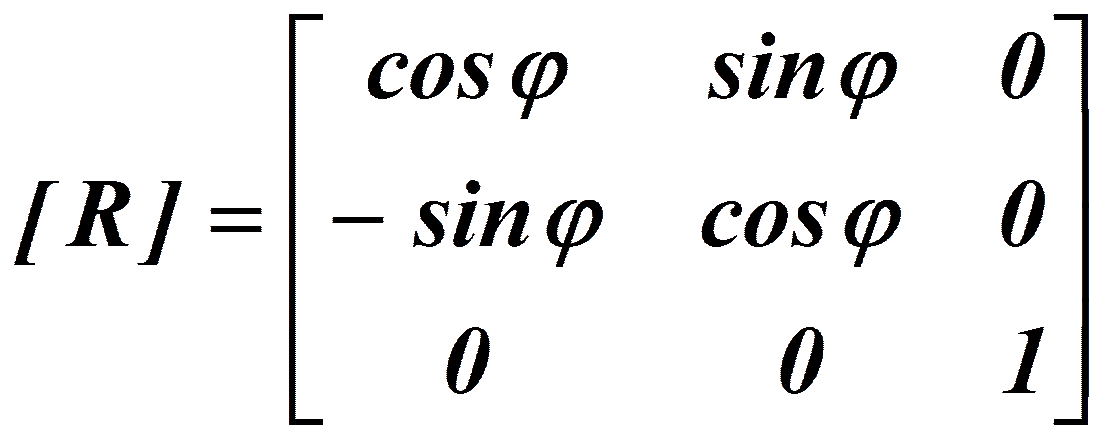