СМО с очередью и приоритетом.

n=1 -1 канал. m=2 в очереди 2 места.

Заявка 1 вытесняет заявку 2, если она обслуживается и занимает место в очереди перед ней, если она стоит в очереди. Вытесненная заявка 2 покидает СМО необслуженной, если в очереди нет мест, и становится в очередь если места нет.

Андрей Андреевич Марков
Дата рождения:	14 июня 1856 года
Место рождения:	Рязань
Дата смерти:	20 июля 1922 года
Место смерти:	Петроград
Гражданство:	Россия
Научная сфера:	математика

Ма́рков, Андре́й Андре́евич (14 июня 1856(18560614), Рязань, Россия — 20 июля 1922, Петроград, ныне Санкт-Петербург) — выдающийся русский математик, внёсший большой вклад в теорию вероятности, математический анализ и теорию чисел.

С 13 декабря 1886 года — адъюнкт Физико-математического отделения (чистая математика), с 3 марта 1890 года — экстраординарный академик, а с 2 марта 1896 года — ординарный академик Императорской Санкт-Петербургской Академии Наук.

В 1912 году математик, по собственному настоянию, подвергся отлучению от церкви, после того, как написал, что не усматривает разницы между иконами и идолами^[1]. Отец А. А. Маркова-младшего.

Методика комплексной оценки вариантов построения АСУ.(АОИ)

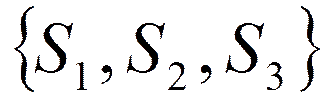- множество вариантов построения

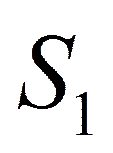- с одним процессором.

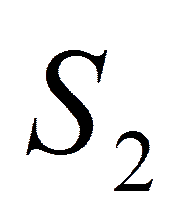- с двумя процессорами.

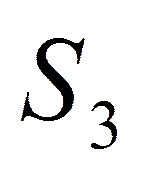- с тремя процессорами.

.

Критерии:

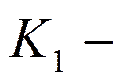среднее время ожидания решения задачи;

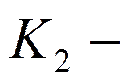коэффициент загрузки;

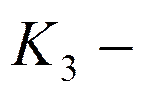пропускная способность (число заданий/сек)

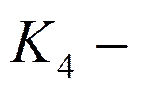вероятность правильного ответа;

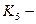стоимость.

Внешние условия :

Число пользователей .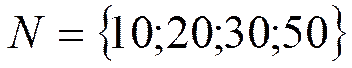

1. Матрица критерий-структура- внешнее условие.

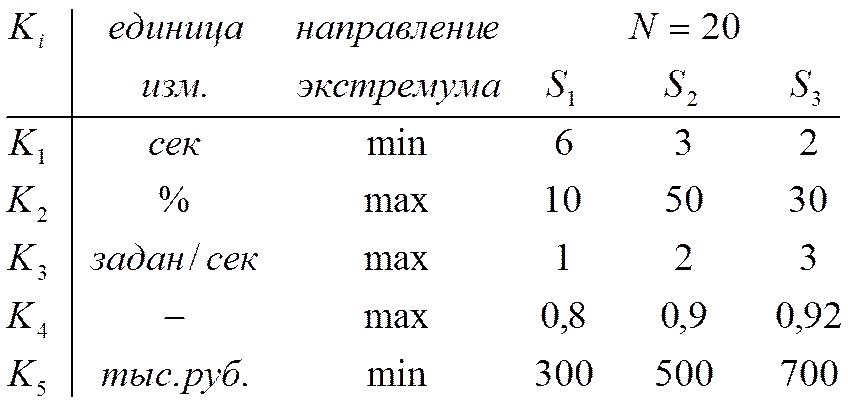
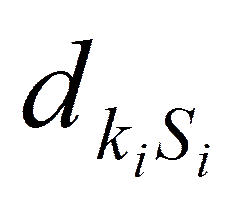- элементы матрицы.

2. Матрица взаимных предпочтений критериев (по экспертным оценкам).

, .

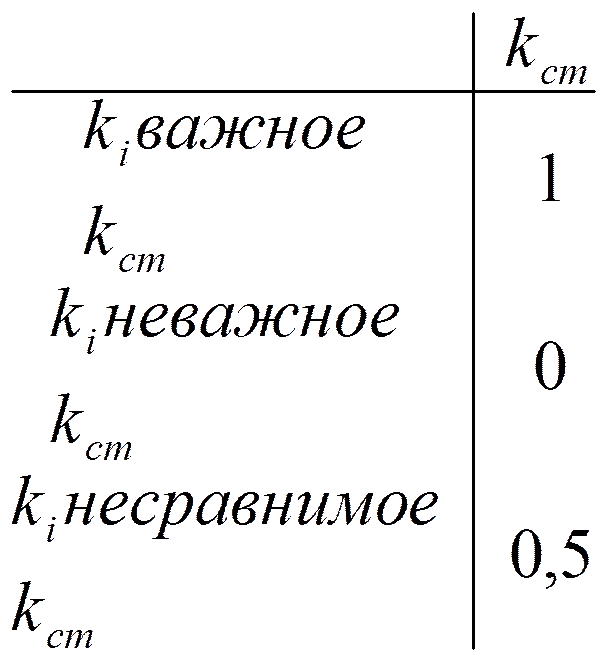
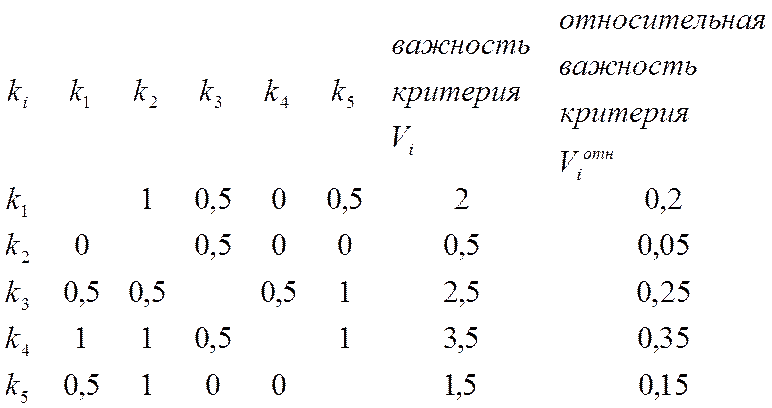
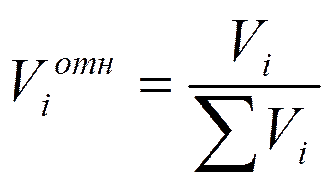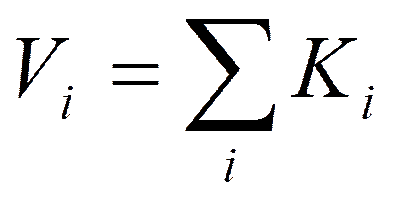3. Матрица чувствительности критериев к выбору варианта.

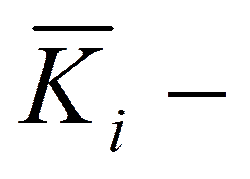среднее значение критерия.

, , , , .

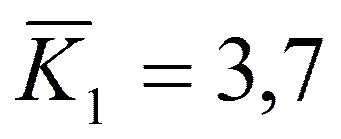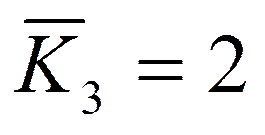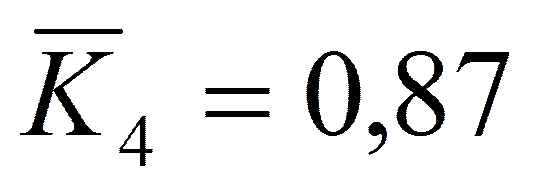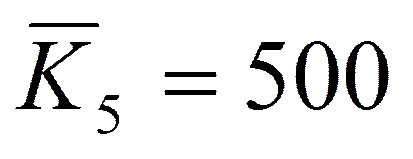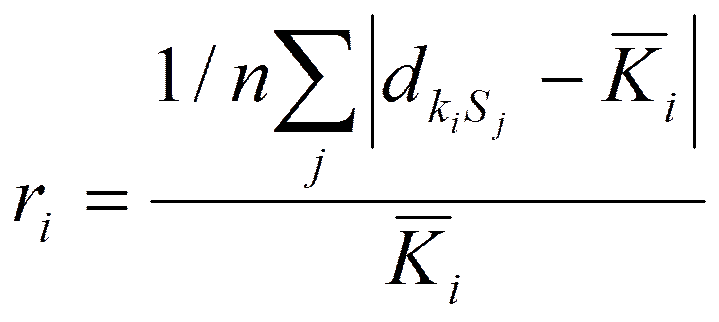, где n-число вариантов.

N=20.

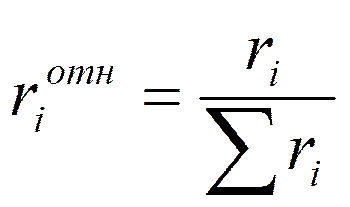
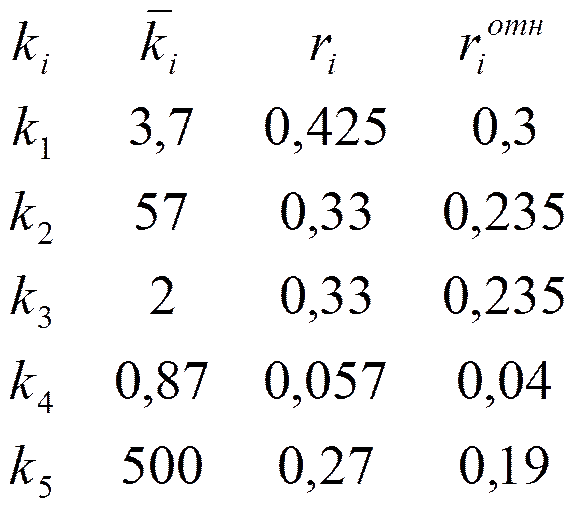
4. Средняя относительная важность критерия.

; , , , .

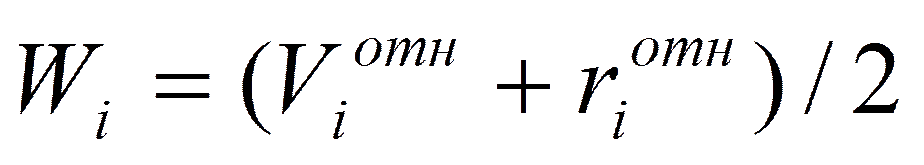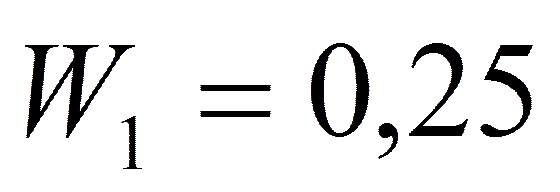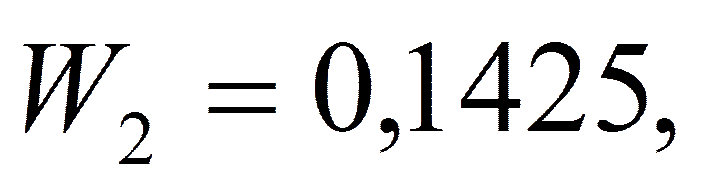
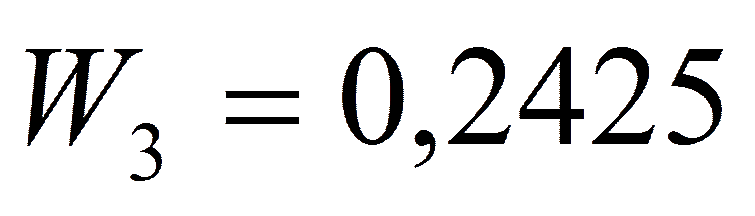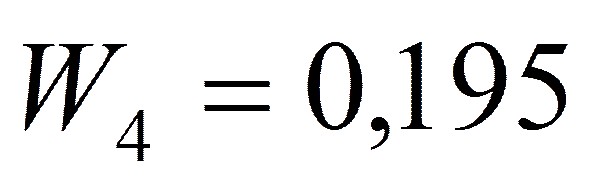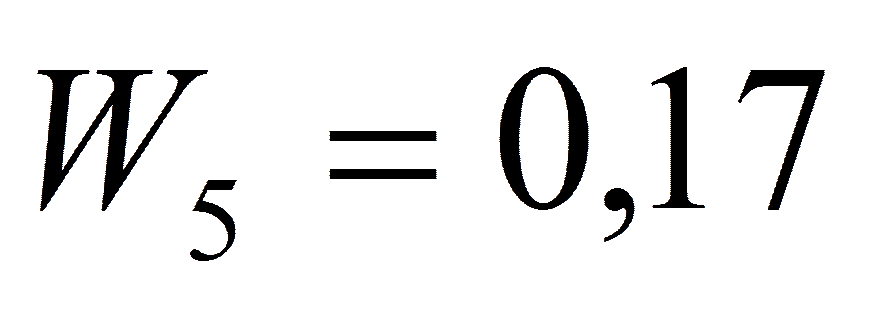Проверяется условие: 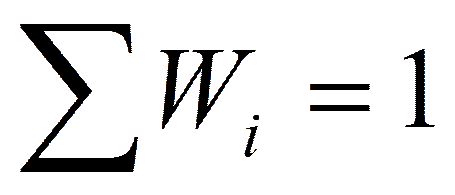, т.е. 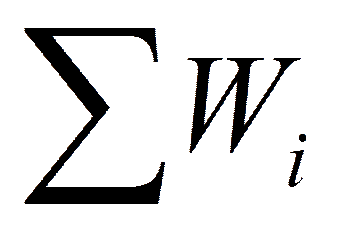- нормирующий коэффициент.

5. Взвешенная матрица- «критерий-структура- внешнее условие».

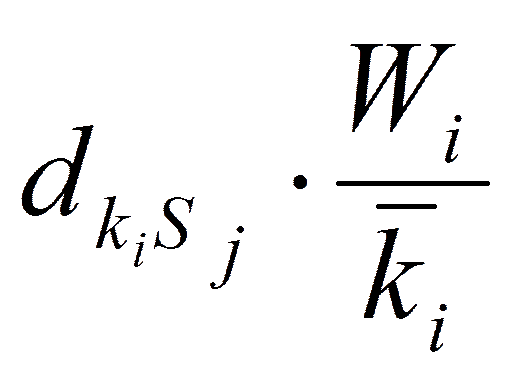, т.е. коэффициент строки умножается на .

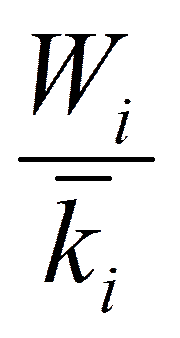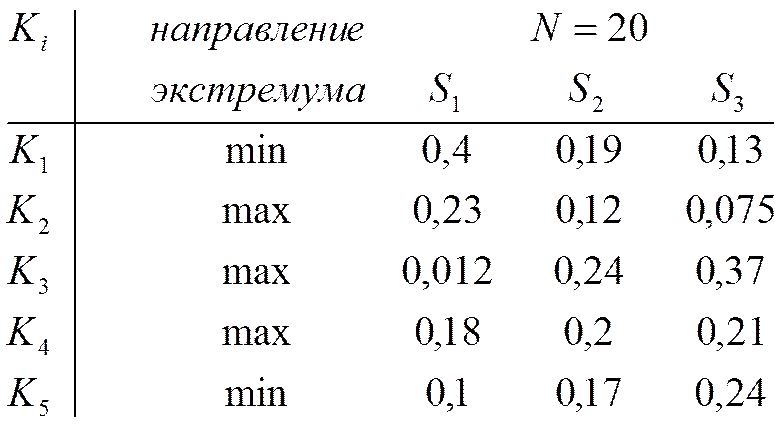
6. Оценка эффективности АСУ для каждого варианта :

N=20

, , , .

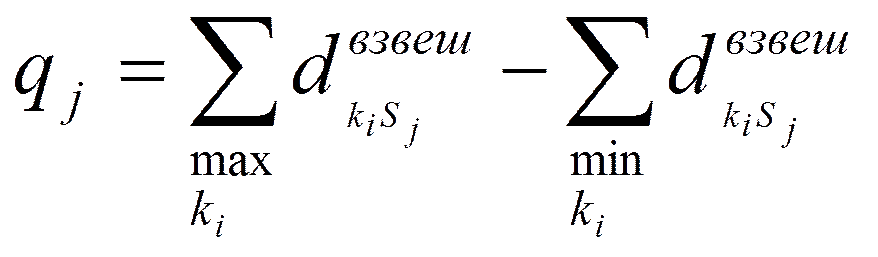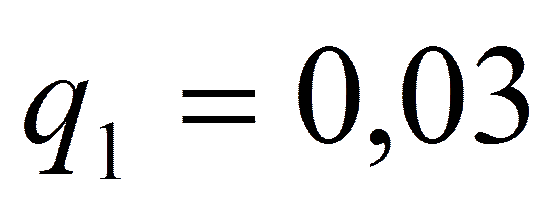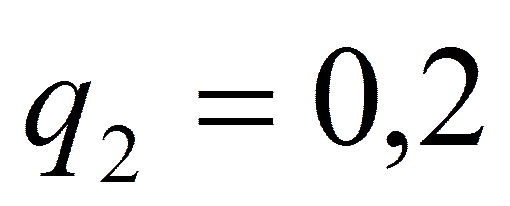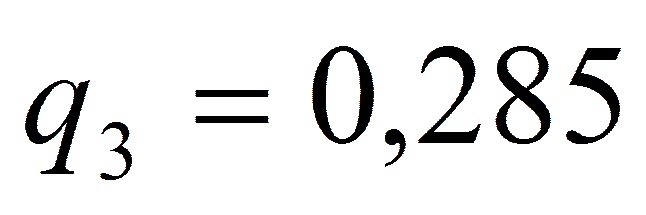7. Матрица эффективности для различных внешних условий.

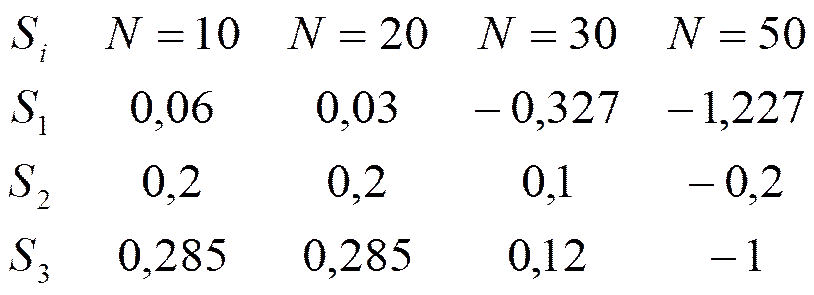
8. Оцениваются «вероятности» внешних условий.

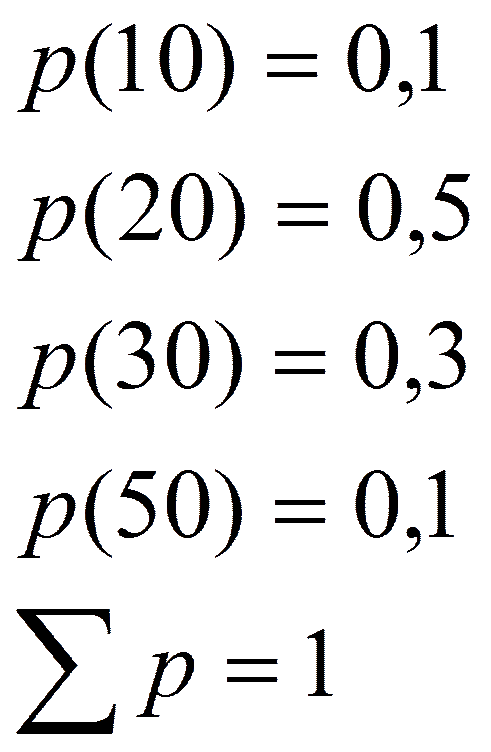
9. «Математическое» ожидание эффективности структуры.

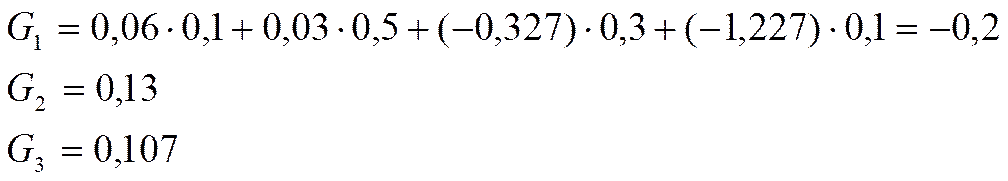
Наиболее рациональной является структура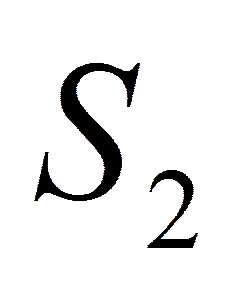

Требования к обработке цифровых информационных массивов

Тенденции к росту объемов информационных массивов и повышению требований к

точности и полноте их обработки за минимальное время заставляют разработчиков новых

информационных систем наращивать их вычислительные мощности. Непрерывное

увеличение быстродействия вычислительных комплексов ведет к росту стоимости

обработки информации, далеко не всегда обеспечивая выполнение требуемых условий

обработки данных.

Таким образом, в настоящее время остается актуальной задача создания новых

методов обработки данных, которые, наряду с обеспечением заданной точности и

скорости обработки, не требовали бы обязательного увеличения мощности

вычислительных комплексов.

Широкое распространение цифровых вычислительных машин объясняется,

главным образом, универсальностью цифровых расчетов и высоким быстродействием

современных ЭВМ. Кроме того, наличие сравнительно недорогих персональных ЭВМ

различной мощности обусловило превращение цифровых расчетов фактически в

единственную вычислительную технологию. В то же время, непрерывное усложнение

большинства решаемых задач, необходимость во многих случаях многократной цифровой

обработки массивов данных сводит к минимуму достижения по увеличению

быстродействия цифровых ЭВМ. С другой стороны, в сложившейся ситуации

представляется явно недостаточным использование достижений отраслей чистой

математики (анализа, геометрии, алгебры и т.д.) при создании алгоритмического и

программного обеспечения. Выполнять же на цифровой технике аналитические

преобразования и выводы формул на основе математических закономерностей при

определении характеристик сложных объектов различной физической природы весьма

затруднительно и неудобно для дальнейшего использования.

В лекции описаны результаты поиска возможных путей совмещения

цифровых расчетов с аналитическими преобразованиями и выводами с целью повышения

точности и скорости вычислений на ЭВМ. При этом сохраняется наглядность

аналитических выводов и возможность на каждом шаге вычислений иметь аналитическое

представление вычисляемых характеристик, искомых параметров и оценок.

Успешная реализация комбинированного метода обработки данных

непосредственно зависит от формы аналитического описания исходных числовых

массивов. Анализ возможных методов получения аналитического описания показал

что наиболее полно поставленным условиям отвечает метод, основанный на

аппроксимации данных отрезками ортогональных рядов с использованием классических

ортогональных полиномов и функций непрерывного и дискретного аргументов , вейвлетов.

Замечательные аппроксимативные свойства ортогональных базисов определяют их

привлекательность при решении указанных ранее задач, а использование результатов

аппроксимации в разнообразных аналитических преобразованиях и выводах для

получения требуемых оценок или характеристик делают классические ортогональные

базисы перспективным инструментом в имеющемся множестве методов и подходов

аналитического описания цифровых информационных массивов.

Теория классических ортогональных базисов есть обобщение теории рядов Фурье на

алгебраические полиномы. Их отличительная особенность состоит, главным образом, в

том, что в большинстве формул, задающих конкретные базисы, имеются параметры,

изменение которых может заметно менять свойства ортогональных полиномов и весовых

функций, образующих конкретный ортогональный базис. Последнее обстоятельство

особенно важно в задачах оптимальной аналитической аппроксимации, когда заданная

точность должна быть обеспечена наиболее коротким отрезком ортогонального ряда.

Применение специальных адаптивных процедур обеспечивает оптимальную

(квазиоптимальную) аналитическую аппроксимацию данных на цифровых ЭВМ в

автоматическом режиме. Появляется реальная возможность весьма эффективно проводить

разнообразные аналитические преобразования и выводы, способствующие получению в

аналитической форме необходимых оценок и характеристик.

Наряду с теоретическими основами, рассмотрим примеры

применения обобщенного спектрально-аналитического метода при решении широкого

круга прикладных задач, прежде всего задач диагностики.

Так как обобщить метод на функции двух переменных оказалось сложно,

дальнейшее его развитие для данных проблем шло по пути использования

параметрического описания плоских и пространственных изображений. При этом плоские

изображения описываются системой из двух уравнений одного переменного, а

пространственные конфигурации однозначно определяются системой из трех уравнений

одного переменного. При таком подходе требуется векторизация поступающего

изображения, т.е. представление его математического описания в параметрической форме

в виде системы уравнений одного аргумента. В дальнейшем анализе полностью

применимы алгоритмы и программы, наработанные для одномерных функций одного

аргумента. В этом случае признаками объекта выступают коэффициенты

разложения проекций по наиболее подходящему ортонормированному базису из числа

классических.

Вычислительная технология обеспечивает высокое быстродействие

при решении информационных задач, требуемую точность вычислений и их наглядность

при сравнительно небольшой стоимости таких вычислителей за счет распараллеливания

операций и высокой унификации блоков, их образующих. Программирование для

решения разнообразных задач на универсальных вычислителях будет сведено к минимуму

за счет предварительного выполнения аналитических преобразований и выводов в

пространстве коэффициентов разложения.

**********************************************************

Анализ методов обработки цифровых информационных массивов

Развитие современных универсальных ЭВМ подчинено главным образом

увеличению скорости выполнения вычислительных операций за счет увеличения тактов частоты центрального процессора и распараллеливания вычислительных процедур.

Такое направление развития вычислительной техники требует высокоразвитой технологической базы, налаженного производственного процесса, а также больших материальных затрат при создании и эксплуатации ЭВМ новых поколений.

Однако даже новейшие супер-ЭВМ, вероятнее всего, не внесут принципиальных изменений в процесс цифровой обработки сигналов.

Эффективная обработка поступающей измерительной информации для обеспечения оперативного решения широкого круга прикладных задач будет определяться выполнением следующих основных требований к математическому обеспечению и средствам обработки данных:

- способность перерабатывать большой объем поступающей

информации за минимальное время в условиях жестких ограничений по

энергопотреблению, массе и габаритам, обеспечивая при этом высокую

производительность вычислительных устройств и требуемую точность вычислений;

-возможность распараллеливания вычислительных операций для их реализацию на ЭВМ новых поколений;

-помехоустойчивость используемых алгоритмов.

Кроме того, разрабатываемые математические приемы должны обеспечивать эффективность и устойчивость решения некорректно поставленных задач, в том числе в задачах диагностики, анализа изображений и распознавания образов.

Рассмотрим соотношения между числовыми и аналитическими способами обработкиданных, исходя из основных требований, предъявляемых к методам обработкиинформационных массивов.

Под информационным (цифровым) массивом будем пониматьупорядоченную совокупность цифровых значений конечной размерности, отображающую определенные характеристики или зависимости об изучаемом объекте или явлении.

Извлечению полезной информации из поступающих на ЭВМ информационных массивов служат существующие и разрабатываемые вновь методы, способы и алгоритмы обработки данных.

Проведем сравнительный анализ эффективности решения всего комплекса задач существующими способами и возможными формами хранения информации.

Бурное развитие цифровой вычислительной техники в США обусловило вполне удовлетворительное обеспечение потребителей цифровыми ЭВМ и привело к тому, что при проведении научно-исследовательских работ цифровые расчеты стали основным способом решения всевозможных математических задач практически во всех областях науки и техники. Этому также в значительной степени способствовало развитое математическое обеспечение, наличие больших программных комплексов для решения разнообразных задач.

В нашей стране сложились другие условия.

Нехватка необходимых вычислительных мощностей, а также сложившиеся традиции русской математической школы привели к тому, что в Советском Союзе и теперь в России основные усилия ученых и специалистов были сосредоточены на использовании аналитических методов при решении задач.

На первом этапе уделялось большое внимание наиболее полному математическому описанию исследуемых объектов.

Затем проводились аналитические исследования, преобразования и упрощения исходных аналитических соотношений за счет обоснованных допущений для выявления основных свойств изучаемых объектов и явлений в целом.

Такой подход обусловил необходимость тщательного выбора математического аппарата при проведении

конкретных исследований, аккуратной и тонкой работы с аналитическими

соотношениями, продумыванию каждого последующего шага преобразований, чтобы, не нарушая заданных условий, получить ответ, адекватно отображающий изучаемое явление в определенном диапазоне допущений.