Алгоритм перехода к новому координатному базису в многомерном пространстве.

Для аппроксимации информационных множеств прямоугольными параллелепипедами используются алгоритмы перехода от одного базиса к другому [Изв. АН СССР. Техн. кибернет., 1983, №2, с. 94-102]. Поскольку аппроксимация прямоугольными параллелепипедами является основой алгоритма последовательного визуального решения задач математического программирования рассмотрим этот вопрос подробнее.

Пусть в пространстве 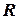имеются два базиса: старый 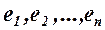и новый 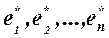. Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса [Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер и др. М.: ЮНИТИ, 2001. – 471с.]:

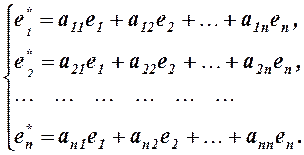(1)

Полученная система означает, что переход от старого базиса 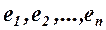к новому 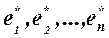задается матрицей перехода 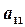и т.д.

,

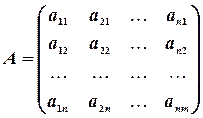причем коэффициенты разложения новых базисных векторов по старому базису образуют столбцы этой матрицы.

Матрица 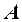– неособенная, так как в противном случае ее столбцы (а следовательно, и базисные векторы) оказались бы линейно зависимыми. Обратный переход от нового базиса 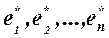к старому базису 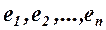осуществляется с помощью обратной матрицы .

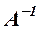Найдем зависимость между координатами вектора в разных базисах. Пусть рассматриваемый вектор 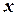имеет координаты 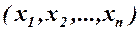относительно старого базиса и координаты 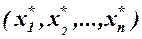относительно нового базиса, т.е.

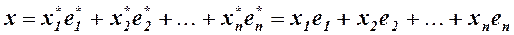. (2)

Подставив значения 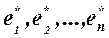из системы (1) в левую часть равенства (2), получим после преобразований:

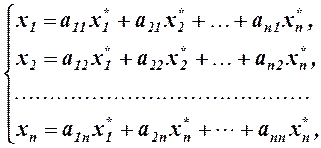
т.е. в матричной форме

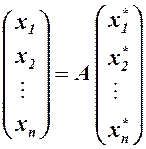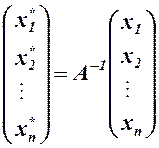или . (3)

Пример. В базисе 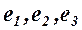заданы вектора 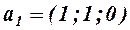, 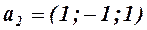и 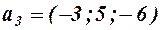. Вектор 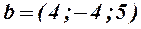, заданный в базисе 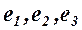, выразить в базисе .

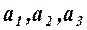Решение. Выразим связь между базисами:

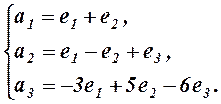
Матрица перехода от базиса 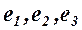к базису 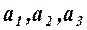имеет вид

.

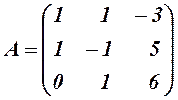Вычисляем 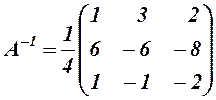. Рассмотрим получение обратной матрицы 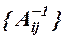для матрицы :

,

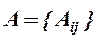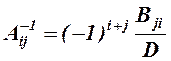где 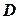– определитель исходной матрицы 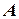, 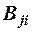- определитель матрицы, полученной из матрицы 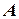, вычеркиванием 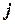– строки и 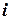– столбца.

Теперь по (3)

,

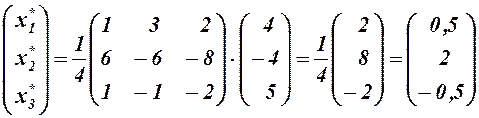т.е. новые координаты вектора 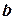в базисе 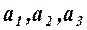есть 0,5; 2 и –0,5 и вектор 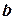может быть представлен в виде:

.

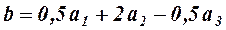Для некоторых функций остановка (или большое количество итераций) по методу Гаусса-Зайделя может произойти при наличии «оврагов». Тогда применяютовражный метод минимизации с помощью метода Гаусса-Зайделя (метод минимизации при наличии оврагов)

В овражном методе производится минимизация функции при различных начальных условиях. Оптимальные точк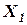и и 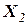определяют новое направление минимизации. Движение осуществляется к точке 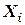c наименьшим значением функции.

Формирование движения по прямой в многомерном пространстве:

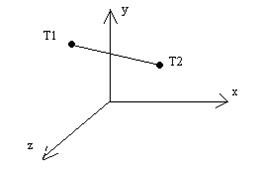
Рис. 2.

Точка 1: 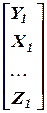. Точка 2: .

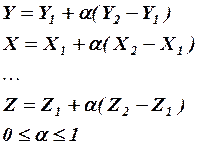
Алгоритм преобразования фигуры в плоскостных координатах

Пусть M - произвольная точка на плоскости с координатам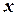и и 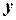, вычисленными относительно заданной прямолинейной координатной системы. Однородными координатами этой точки называется любая тройка одновременно не равных нулю чисел 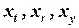связанных с заданными числам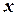и и 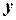следующими соотношениями:

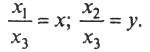
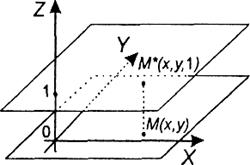
Рис. 6. Преобразование координат точки на плоскости в однородные координаты

При решении задач компьютерной графики однородные координаты обычно вводятся так: произвольной точке 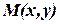на плоскости ставится в соответствие точка 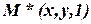в пространстве (рис. 6).

Заметим, что производная точка на прямой, соединяющей начало координат, точку 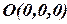, с точкой 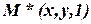, может быть задана тройкой чисел вида 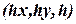. Будем считать, что 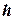неравно 0.

Вектор с координатами 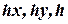является направляющим вектором прямой, соединяющей точк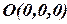и и 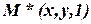. Эта прямая пересекает плоскость 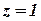в точке 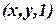, которая однозначно определяет точку 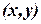координатной плоскости .

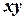Тем самым между произвольной точкой с координатами 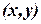и множеством троек чисел вида 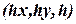, при 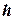неравной 0, устанавливается (взаимно однозначное) соответствие, позволяющее считать числа 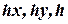новыми координатами этой точки.

В проективной геометрии для однородных координат принято следующее обозначение: 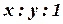или, более обще, 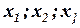(напомним, что здесь непременно требуется, чтобы числа 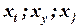одновременно в нуль не обращались).

Применение однородных координат оказывается удобным уже при решении простейших задач.

Рассмотрим, например, вопросы, связанные с изменением масштаба. Если устройство отображения работает только с целыми числами (или если необходимо работать только с целыми числами), то для произвольного значения 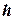(например, 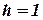) точку с однородными координатами 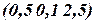представить нельзя. Однако при разумном выборе 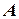можно добиться того, чтобы координаты этой точки были целыми числами. В частности, при 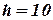для рассматриваемого примера имеем .

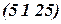Рассмотрим другой случай. Чтобы результаты преобразования не приводили к арифметическому переполнению, для точки с координатами 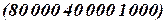можно взять, например, 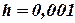. В результате получим .

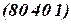Приведенные примеры показывают полезность использования однородных координат при проведении расчетов. Однако основной целью введения однородных координат в компьютерной графике является их несомненное удобство в применении к геометрическим преобразованиям.

При помощи троек однородных координат и матриц третьего порядка можно описать любое аффинное преобразование плоскости.

В самом деле, считая 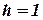, сравним две записи: помеченную символом * и нижеследующую, матричную:

.

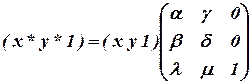Нетрудно заметить, что после перемножения выражений, стоящих в правой части последнего соотношения, мы получим обе формулы (*) и верное числовое равенство .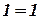

Тем самым сравниваемые записи можно считать равносильными.

Элементы произвольной матрицы аффинного преобразования не несут в себе явно выраженного геометрического смысла. Поэтому чтобы реализовать то или иное отображение, т.е. найти элементы соответствующей матрицы по заданному геометрическому описанию, необходимы специальные приемы. Обычно построение этой матрицы в соответствии со сложностью рассматриваемой задачи и с описанными выше частными случаями разбивают на несколько этапов.

На каждом этапе ищется матрица, соответствующая тому или иному из выделенных выше случаев А, Б, В и Г, обладающих хорошо выраженными геометрическими свойствами.

Выпишем соответствующие матрицы третьего порядка.