Теоретические основы метода максимально правдоподобия

Разные методы оценивания одних и тех же параметров могут давать разные результаты. Когда есть несколько путей к одной цели, естественно, хочется выбрать наилучший. При определенных ограничениях таким методом является метод максимального правдоподобия, основанный на оптимальном использовании имеющейся в выборке информации о параметрах распределения[10].

Пусть X₁,…, X_n – выборка из распределения, плотность которого в точке x зависит от неизвестного параметра θ. Обозначим плотность отдельного наблюдения X_i (i = 1,…,n) через f(x, θ). Поскольку случайные величины X₁,…, X_n независимы, плотность вероятностей вектора (X₁,…, X_n) равна

f(x₁, θ) f(x₂, θ)…f(x_n, θ), (6.1)

где θ – неизвестное нам истинное значение параметра.

Метод максимального правдоподобия состоит в следующем. Подставим в (6.1) вместо переменных (x₁,…,x_n) элементы выборки, т.е. реализации случайных величин X₁,…,X_n, в параметр θ в (6.1) будем рассматривать как случайную величину, изменяющуюся в заданной области значений. В таком случае плотность (6.1) превращается в величину, которую мы будем называть правдоподобием:

f(X₁, θ) f(X₂, θ)…f(X_n, θ). (6.2)

Оно, естественно, является функцией переменного θ. Метод максимального правдоподобия рекомендует выбирать в качестве оценки 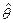некоторого истинного значения параметра θ из (6.1) такое значение, при котором правдоподобие достигает максимума:

f(X₁, θ) f(X₂, θ)…f(X_n, θ) .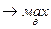

Ясно, что такой выбор 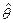происходит в зависимости от значений X₁,…, X_n, поэтому 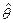является функцией от X₁,…, X_n , т.е. случайной величиной.

Пример: применение к нормальной модели. Прежде чем обсуждать теоретические свойства метода максимального правдоподобия, рассмотрим его действия на примере нормальной выборки N(a,b). В этом случае функция правдоподобия равна

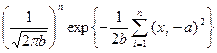. (6.3)

надо выбрать параметры a и b, так, чтобы выражение (6.3) было максимальным (при заданных значениях x₁,…,x_n). Заметим, что при произвольном фиксированном значении b выражение (6.3) будет иметь наибольшее из возможных для него значений, если 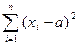примет максимальное значение (относительно а), это произойдет при 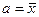. Следовательно, оценка максимального правдоподобия 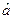для а равна .

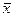Для того, чтобы найти оценку максимального правдоподобия параметра b, вычислим .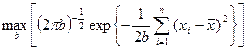

Эта задача без труда решается при помощи средств математического анализа. (Надо взять производную по b, приравнять ее к нулю и решить полученное уравнение относительно b). После всех вычислений получим .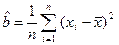

Итак, оценка максимального правдоподобия для (a, b) равна

.

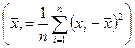Пояснения к методу. Попытаемся выяснить теоретическую причину метода максимального правдоподобия: почему при больших n полученные этим методом оценки параметра θ в (1.1.1) близки к его истинному значению, и как в этом участвует закон больших чисел.

Отметим, что функция f(X₁,θ)…f(X_n, θ) и

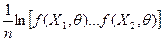(6.4)

достигают максимума при одном и том же значении θ, так как логарифм является монотонно возрастающей функцией. Представив логарифм произведения в виде суммы логарифмов, получаем, что для нахождения оценки максимального правдоподобия можно искать такое значение θ, при котором выражение

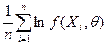(6.5)

достигает максимума.

По закону больших чисел, выражение (6.5) как среднее арифметическое независимых одинаково распределенных величин сходится к их математическому ожиданию, т.е. при больших n оказывается близким к M lnf(X_i, θ). Поэтому оценка максимального правдоподобия близка к такому значению параметра θ, при котором величина M lnf(X_i, θ) достигает максимального значения как функция θ. Остается только найти значение параметра.

Метод максимального правдоподобия имеет ряд достоинств: оценки максимального правдоподобия, вообще говоря, состоятельны (если число признаков невелико), но они могут быть смещенными, распределены асимптотически нормально (при больших значениях n приближенно нормальны) и имеют наименьшую дисперсию по сравнению с другими асимптотически нормальными оценками. Этот метод наиболее полно использует данные выборки об оцениваемом параметре, поэтому он особенно полезен в случае малых выборок. Недостаток метода состоит в том, что он часто требует сложных вычислений.

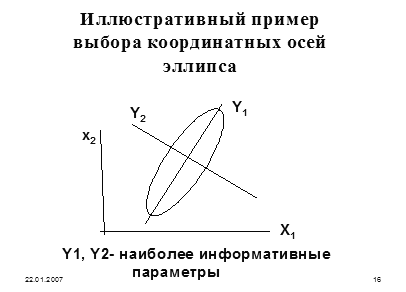
Рис. 1.