Аксиомы теории вероятностей на основе теоретико-множественного подхода

Впервые они были введены А.Н. Колмогоровым. Событию А ставится в соответствие некоторое число, называемое вероятностью события.

Аксиома 1. Вероятность любого события заключена между нулем и единицей

.

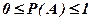Аксиома 2. Если А и В несовместимые события (А × В = Æ), то

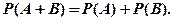(1.9)

Аксиома 3. Вероятность достоверного события равна 1.

.

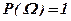Аксиома 4. Сумма вероятностей противоположных событий равна единице

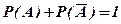(1.10)

Пример 1.5. События А, В могут быть совместимыми (рис. 1.2). Какова вероятность Р(А + В)?

Решение. Непосредственно аксиомой 2 воспользоваться нельзя, т.к. она справедлива лишь для несовместимых событий. Чтобы использовать аксиомы, представим интересующее нас множество в виде суммы несовместимых событий.

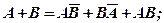(1.11)

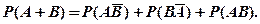(1.12)

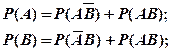
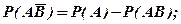(1.13)

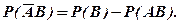(1.14)

Подставляя выражения (I.I3), (I.I4) в (1.12), получаем

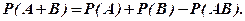(1.15)

Аналогично можно получить формулу для вероятности суммы n совместных событий А₁, А₂, ... А_n.

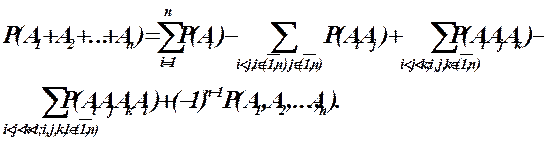(1.16)

Частота или статистическая вероятность события

Определения вероятности в разделах 1.1.1 - 1.1.3 связаны с теоретическим определением вероятности события. Существенная пред­посылка применения рассмотренных методов - условие равновозможности событий. В данном разделе рассматривается метод определения вероятностей событий, пригодный для экспериментальных исследований и не требующий выполнения условий равновозможности события.

Если производится серия из n опытов, в каждом из которых может появиться или не появиться событие А, то частотой события А в данной серии опытов называется отношение числа опытов, в которых появилось событие А, к общему числу n произведенных опытов.

Частоту события часто называют еще статистической вероятностью (в отличие от ранее введенной "математической" вероятности)

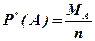(1.17)

Здесь _* - указывает на статистический характер соответствующего параметра, n - число произведенных опытов (не путать с числом случаев в "классической схеме"), М_А- число опытов, в которых событие А появилось.

При большом числе n частота Р*(А) имеет тенденцию стабилизироваться, приближаясь к некоторому постоянному числу. Естественно предположить, что это число и есть вероятность события.

Свойства частот

При любом числе n - большом или малой справедливы следующие соотношения.

1. Правило сложения частот для несовместимых событий.

С = А + В;

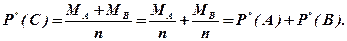(1.18)

2. Правило умножения частот для двух событий.

D = AB;

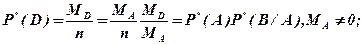
или

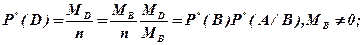
Полученные формулы

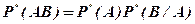(1.19)

или

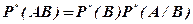(1.20)

имеют очень большое значение. Они показывают, что от одновременного появления двух событий А и В можно перейти к последовательности появления событий: вначале, например, наступает А, а затем - В, при условии, что событие А произошло. Таким образом, с помощью формул осуществляется переход к методу последовательных испытаний. Метод прост, нагляден, позволяет более осмысленно решать сложные вероятностные задачи.

Правило умножения вероятностей легко обобщается на случай произвольного числа событий

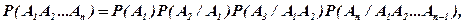(1.21)

т.е. вероятность произведения нескольких событий равна произведение вероятностей этих событий, причем вероятность каждого последующего события вычисляется при условии, что все предыдущие имели место. Для независимых событий формула (1.21) перепишется в виде

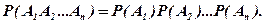(1.22)

Следует подчеркнуть, что, если имеется несколько событий А₁, А₂,…, A_n, то их попарная независимость 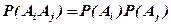еще не означает их независимости в совокупности.

Пример 1.6. В урне 7 шаров: 4 белых и 3 черных. Из нее выни­маются (одновременно или последовательно) два шара. Найти вероят­ность того, что оба они будут белыми. Интересующее событие А = два белых шара.

Решение. Рассмотрим следующие два события: первое - вынима­ние первого шара, второе - вынимание второго шара, при условии, что первый шар вынут из урны. Исходы этих испытаний обозначим d (вынут белый шар) и i (вынут черный шар). Соответствующее про­странство исходов Wизображено на рис.1.3.

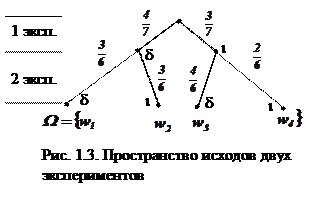
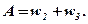
Используя формулы (1.9) и (1.19), (1.20), получаем

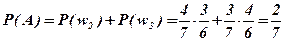
Таким образом, для подсчета вероятностей при проведении экспериментальных исследований основными являются теоретико-множественный и частотный методы. В связи с этим рассмотрим алгоритм подсчета вероятности попадания точки в выпуклую область. Любую невыпуклую область можно представить в виде совокупности выпуклых областей. Например, задана невыпуклая область D (рис.1.4). Эту область можно дополнить до выпуклой добавлением следующей области F, которая является выпуклой. Совокупную область назовем G. Тогда задача сведется к нахождению вероятности попадания в область G и непопадания в область F.Возможен другой подход-разбиение исходной области на выпуклые подмножества.

	D

	F
		G

Рис.1.4. Представление невыпуклой области совокупностью выпуклых областей

Наиболее простым и удобным для практики в описании выпуклых множеств является задание системой линейных неравенств.

ИЗ ”МОИ”: