Выполнение лабораторной работы
Выход
============================================
Выберите пункт меню
Рис. 1. Меню лабораторной работы
3. Рассмотреть вопросы применения метода, изложенного в теоретической части, для конкретных моделей линейных динамических измерительных систем. Кратко это можно изложить так.
В данной лабораторной работе рассматривается итерационный метод восстановления, искаженного линейным оператором сигнала.
В качестве моделей линейной динамической измерительной системы приняты передаточные функции вида:
1. W(p)=1/p
2. W(p)=1/(p+a)
3. W(p)=1/p(p+a)
4. W(p)=1/(p+a1)(p+a2)
5. W(p)=1/(p+a)^2
6. W(p)=1/((p+h)^2+m^2)
с помощью которых могут быть описаны различные классы измерительных систем.
Итерационный процесс имеет вид:
Y(i+1)=Y(i)+(X-AY(i))a
где Х-выходной сигнал (сигнал после искажения)
А-матрица перехода линейного оператора (полученная с помощью одной из квадратурных формул; в данной работе применяется формула прямоугольника)
Y(0)=X
a-величина обеспечивающая сходимость итерационного процесса (в данной работе а=0.1)
Начиная с передаточной функции 3. диагональные элементы матрицы А равны 0 (т.е. в начальный момент времени), что не позволяет восстановить исходный сигнал.
В данной работе используется два метода решения этой проблемы.
1. Восстановление с псевдообращением: в матрице А срезается первая строка и
последний столбец (т.е. диагональные элементы становятся отличными от 0).
2. Восстановление с комб. фильтром: ко всем элементам матрицы А лежащим не выше главной диагонали прибавляется функция вида f(t)=k*exp[-nt] (в лабораторной работе используется функция f(t)=1*exp[-100t]), которая в начальный момент времени не равна 0, а в остальные стремится к 0.
Для ускорения процесса восстановления сигнала,свертку А на Y(i) можно выполнять используя быстрые преобразования (в лабораторной работе используется алгоритм БПФ).
Рассмотрим суть метода:
Ф(2^n)=(1/(2^n))П[I(2^(j-1))*(I(2^(n-j))+b(2^(n-j))][I(2^(j-1))*H2*I(2^(n-j))]
где *-кронекеровское произведение
+-прямая сумма
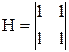 П-произведение от j=n до 1
П-произведение от j=n до 1
b(2^(n-j))=диаг.{1,W^(1·2^(j-1)),W^(2·2^(j-1)),W^(3·2^(j-1)),...}
W=exp(-j2п/8)
Для N=8 (n=3) имеем:
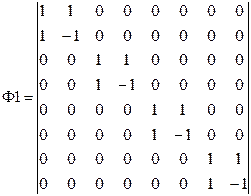
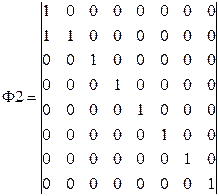
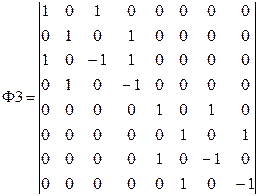
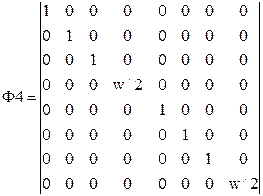
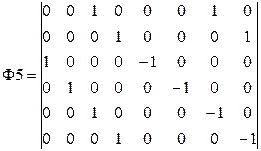
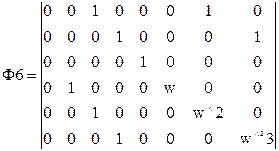
Ф·f=(1/8)·Ф2·Ф1·Ф4·Ф3·Ф6·Ф5·f
F1=(1/8)·Ф·[первый столбец матрицы А]-спектр матрицы перехода
F2=(1/8)·Ф·[Y(i)]-спектр восстанавливаемого сигнала
F=F1·F2
Следовательно свертка, применяя обратное преобразование Фурье, равна
f=F·Ф5°·Ф6°·Ф3°·Ф4°·Ф1°·Ф2°,где °-знак транспонирования.
Затем результат подставляется в основную формулу итеративного метода:
Y(i+1)=Y(i)+(X-AY(i))a
Примечание: в результате БПФ результат получается в двоичном инверсном коде в несортированном виде, но в данной лабораторной работе в результате многократного применения БПФ и использования обратного БПФ результат получается в виде пригодном для дальнейшего использования, т.е. не требуется производить сортировку и переводить инверсный двоичный код в прямой.
Содержание отчета
1 Цель работы и основные теоретические положения.
2 Результаты восстановления искаженного сигнала для различных измерительных систем. Оценка эффективности метода.
3 Изложить возможности использования метода в информационных системах и системах управления.
Библиографический список
1. Клейман Е.Г. Идентификация входных сигналов в динамических системах// АиТ. 1999. №12. С. 3-15.
2. Аш Ж. И др. Датчики измерительных систем. В 2-х книгах. Кн.2: Пер с франц. М.: Мир, 1992. С. 292.
3. Василенко Г.И. Теория восстановления сигналов: от редукции к идеальному прибору в физике и технике. М., 1979. 272 с.
1.Оперативное оценивание параметров модели регрессии
при наличии аномальных результатов измерений(МОИ+АОИ)
В реальных системах обработки информации оценки 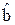 вектора регрессионных коэффициентов b для модели
вектора регрессионных коэффициентов b для модели
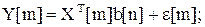
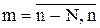 , (38)
, (38)
где X[m] – вектор наблюдаемых линейно независимых факторов;
b – вектор неизвестных и подлежащих оценке параметров;
e[m] – помеха типа белого шума, приходится проводить в условиях аномальных измерений (АИ) Y(l), l Î ( 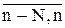 ).
).
Наибольшее распространение при решении поставленной задачи получили метод максимального правдоподобия при известном законе распределения ошибки [10] и метод наименьших модулей (МНМ), обеспечивающий устойчивое решение в условиях отклонения реального закона распределения ошибки от постулируемого априори закона распределения [11,12]. Однако все эти методы требуют в случае обнаружения АИ значительных вычислительных затрат для исключения влияния самих измерений на искомую регрессионную зависимость.
Необходимо организовать процесс вычислений таким образом, чтобы не получать каждый раз результат заново, а корректировать процесс вычислений с учетом аномальности результата измерений. Подобный подход можно применять для обработки как накопленных данных, так и последовательно поступающей порции информации.
4.1. Метод выделения результата АИ
В основу его алгоритма положен итеративный метод решения на основе МНМ [11,13]. При этом оценка 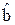 , полученная на основе N результатов измерения, имеет вид
, полученная на основе N результатов измерения, имеет вид
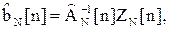 (39)
(39)
где
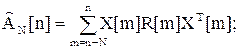 (40)
(40)
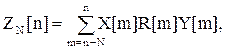 (41)
(41)
где 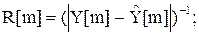
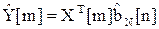 - оценка m-го измерения выходного сигнала.
- оценка m-го измерения выходного сигнала.
Начальные значения R[m]=1; 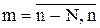 соответствуют определению параметров
соответствуют определению параметров 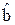 по методу наименьших квадратов (МНК). Далее вычисления оценок по формулам (39) – (41) проводятся итерационно до тех пор, пока изменения оценок за одну итерацию не достигнут заданной малой величины. При этом наименьший весовой коэффициент R[l] указывает на наиболее грубое l-измерение.
по методу наименьших квадратов (МНК). Далее вычисления оценок по формулам (39) – (41) проводятся итерационно до тех пор, пока изменения оценок за одну итерацию не достигнут заданной малой величины. При этом наименьший весовой коэффициент R[l] указывает на наиболее грубое l-измерение.
4.2. Рекуррентная процедура исключения АИ
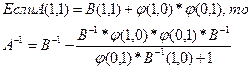
Матрицу 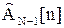 и вектор Zn-1[n] при R[m]=1;
и вектор Zn-1[n] при R[m]=1; 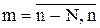 можно определить из
можно определить из 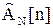 , ZN[n], полученных на первой итерации, путем исключения аномальных составляющих
, ZN[n], полученных на первой итерации, путем исключения аномальных составляющих

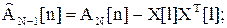 (42)
(42)
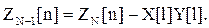 (43)
(43)
На основании леммы об обращении матриц можно записать
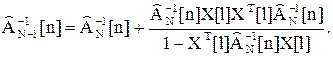 (44)
(44)
Используя выражения (43) и (44), получаем
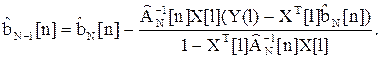 (45)
(45)
