Решение задач, появляющихся в случайные
Моменты времени.(АОИ)
Задачи отличаются режимом обслуживания заявок.
Одноканальные системы массового обслуживания с отказами.
Вначале перечислим все возможные состояния системы:
S0 – канал свободен,
S1 – канал занят.
Под действием потока заявок, система меняет свое состояние.
λ– поток заявок.
Интенсивность:
λ = 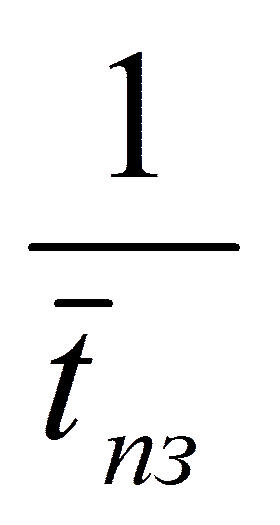
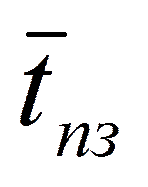 - среднее расстояние между двумя заявками.
- среднее расстояние между двумя заявками.
Под действием потока решений μ система из S1 возвращается в состояние S0.
μ = 
μ – интенсивность потока решений.
Для данной системы составим уравнение
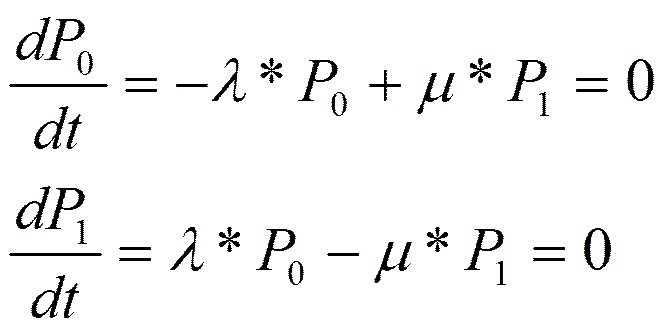
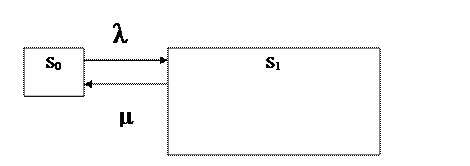
В левой части ставим производную для состояния. В правых частях уравнения столько слагаемых, сколько стрелок связано с данным состоянием. Если стрелка выходит из состояния, соответствующее слагаемое берем со знаком минус, а если входит в соответствующее состояние, то со знаком плюс. Каждое слагаемое равно произведению интенсивности потока, соответствующая стрелке, на вероятность того состояния, из которого выходит стрелка. К этим уравнениям добавляется уравнение нормировки:
р0+р1=1.
Как правило рассчитывается установившийся режим системы, когда все произведения равны нулю.
Пример:
Возьмем λ=1, μ=1.
Получаем систему, в которой всегда можно удалить одно уравнение.
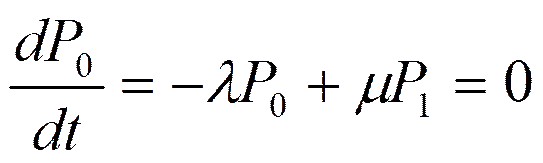 ,
,
р0+р1=1.
Получили 2 уравнения с двумя неизвестными. Вероятность последнего есть вероятность отказа в выполнении заявки.
Многоканальная система массового обслуживания (СМО)
Имеем 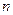 каналов.
каналов.
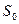 -заявок нет, машина свободна.
-заявок нет, машина свободна.
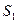 -1 заявка, одна машина занята, остальные свободны.
-1 заявка, одна машина занята, остальные свободны.
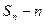 заявок, все
заявок, все 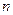 машины заняты.
машины заняты.
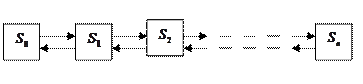
Составляем уравнение Колмогорова:
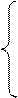
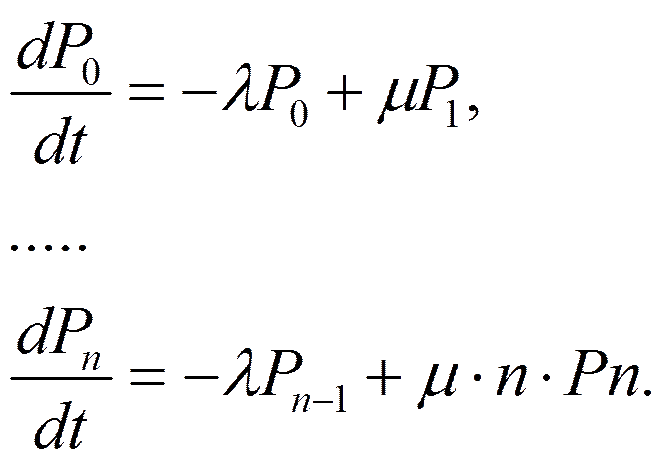
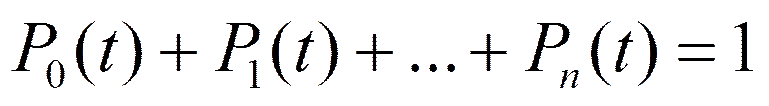
Одно уравнение в системе надо удалить. Его удаляют и используют для контроля.
Многоканальная система массового обслуживания (СМО) с ожиданием.
Возьмем n каналов, m- длина очереди заявок.
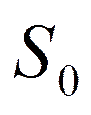 -заявок нет, машина свободна, очереди нет.
-заявок нет, машина свободна, очереди нет.
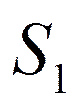 -одна заявка, одна машина занята, остальные свободны, очереди нет.
-одна заявка, одна машина занята, остальные свободны, очереди нет.
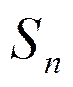 - n -заявок, n -машин заняты, очереди нет.
- n -заявок, n -машин заняты, очереди нет.
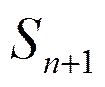 - n+1 -заявок, n -машин заняты, одна заявка в очереди.
- n+1 -заявок, n -машин заняты, одна заявка в очереди.
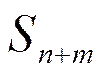 -n+m- заявок, n -машин заняты, m -заявок в очереди.
-n+m- заявок, n -машин заняты, m -заявок в очереди.
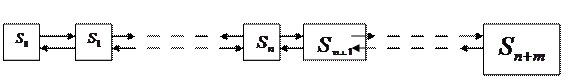
Сравним время ожидания : 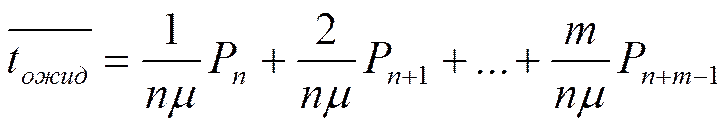
Замкнутое СМО.
Дано:
n-кафедр,
m – ЭВМ,
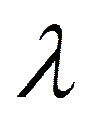 - поток заявок,
- поток заявок,
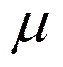 - поток решений.
- поток решений.
Кафедра, подавшая заявку не обслуживается до тех пор, пока не будет выполнена ее 1-ая заявка.
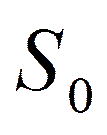 - заявок нет, ЭВМ свободны, очереди нет.
- заявок нет, ЭВМ свободны, очереди нет.
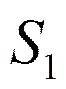 -1-ая заявка, 1 ЭВМ занята, очереди нет.
-1-ая заявка, 1 ЭВМ занята, очереди нет.
…..
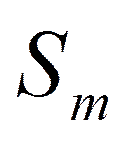 - m заявок, m – ЭВМ, очереди нет.
- m заявок, m – ЭВМ, очереди нет.
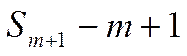 заявка, , m – ЭВМ занято, 1 заявка в очереди.
заявка, , m – ЭВМ занято, 1 заявка в очереди.
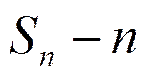 заявок, m – ЭВМ занято, n-m в очереди.
заявок, m – ЭВМ занято, n-m в очереди.

Характеристики системы:
Определим среднее число заявок в системе -
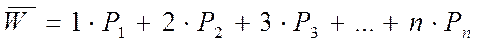
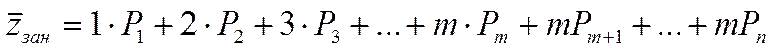
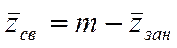 - свободных.
- свободных.
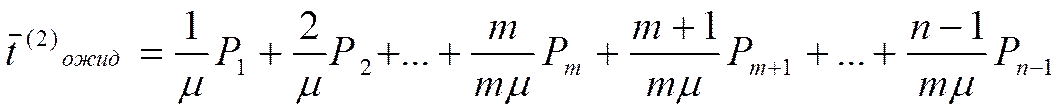
- время ожидания подачи второй заявки.
Среднее число заявок в очереди - 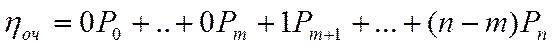 .
.
Выбор оптимального значения числа ЭВМ
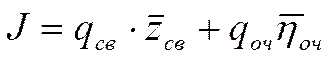 ,
, 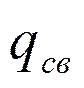 - потери, связанные с простоем машины;
- потери, связанные с простоем машины; 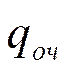 - потери,связанные с простоем заявки в очереди.
- потери,связанные с простоем заявки в очереди.
**********************************************************************
Система массового обслуживания с взаимопомощью между каналами.
СМО с отказами:
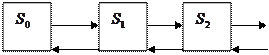 |  | ||||||||
 |  |  | |||||||
 |  |  | |||||||
СМО с ожиданием :
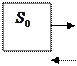 |  | 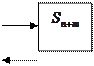 | |||||||||||||
 |  |  | |||||||||||||
 |  |  |  | ||||||||||||
