Выявление уровня знаний младших школьников об математических отношениях при изучении математики
Констатирующий эксперимент — это строго контролируемое педагогическое наблюдение, где исследователь экспериментальным путем устанавливает только состояние изучаемой педагогической системы, констатирует факт связи, зависимости между явлениями. В констатирующем эксперименте мы выявим критерии, показатели и уровни сформированности у младших школьников …..
Цель констатирующего эксперимента: выявить уровни знаний младших школьников об математических отношениях. Для этого был провден эксперимент в МБОУ СОШ № 27 4 «а» классе у 27 учащихся, учитель Розина Ирина Сергеевна, УМК «Планета знаний».
Задачи констатирующего эксперимента:
-выявить критерии и показатели уровня знаний младших школьников обматематических отношениях;
-сформировать на основе выделенных критериев и показателей характеристику уровней;
-подобрать методики для выявления уровня знаний младших школьников об математических отношениях;
-провести методики в 4 «а» классе МБОУ СОШ №27 г. Череповца;
-сделать количественный и качественный анализ полученных результатов.
Для начала определим критерии и показатели уровня знаний младших школьников об математических отношениях, которые представлены в таблице 1.
Таблица 1
Критерии и показатели уровня знаний младших школьников об математических отношениях
| Критерии | Показатели | Методики |
| Мотивационный | Понимание понятий множество, неравенство и равенство. Выделять их существенные признаки. | Методика 1 |
| Когнитивный | Знание основных приемов решения равенств, неравенств и множеств. Выполнение всех операций над множествами, равенствами и неравенствами. | Методика 2 |
| Деятельностный | Умение объяснять как правильно выполнить различные операции над множествами, равенствами и неравенствами. Выделять ошибки и исправлять их. | Методика |
На основе выделенных критериев и показателей, были разработаны методики и составлена характеристика уровней знания младших школьников об математических отношениях, представлены в таблице 2.
Таблица 2
Уровни знаний младших школьников об математических отношениях
| Уровни | Качественная характеристика |
| Высокий | Младший школьник на отлично знает определения всех понятий (равенство, неравенство, множество), выделяет существенные признаки понятий. Знает все основные приемы решения равенств, неравенств. Выполняет хорошо все операции над множествами. Легко находит ошибки в решенных заданиях и сразу исправляет их. Объясняет решение заданий. |
| Средний | Младший школьник знает определения понятий, но не может выделить существенные признаки. Не всегда правильно решает задания связанные с этими понятиями. Не всегда находит ошибки в решенных заданиях и не сразу их исправляет. Знает как выполнять то или иное задание, но сомневается в действиях. Не всегда объясняет как решил то или иное задание. |
| Низкий | Младший школьник забывает определение понятий, не может выделить существенные признаки. При решение заданий связаных с этими понятиями, ему трудно. Не может найти ошибки в решение. Не может объяснить как решил это задание. |
Методика 1. Основные понятия.
Цель: выявить уровень знания младших школьников о математических понятиях у учащихся 4 «а» класса МБОУ СОШ№27 г. Череповца
Содержание: Соотнести понятия с их определениями и подчеркнуть существенные признаки в определениях.
| Равенство | В математике группа предметов или живых существ, собранных вместе |
| Множество | Называют два выражения, соединеных знаком «=» |
| Неравенство | Часть множества |
| Подмножество | Предметы или живые существа, входящее в множество |
| Элементы множества | Называют два выражения, соединеных знаком < или >. |
Оборудование: лист А4 с понятиями и определениями, ручка или карандаш.
Обработка результатов:
Максимальное количество баллов, которое может получить школьник за выполнение задания — 5 баллов.
Интерпретация полученных результатов производится следующим образом:
5 баллов — высокий уровень;
4 балла — средний уровень;
3-0 баллов — низкий уровень.
Полученные результаты методики 1 представлены в таблице 3 в приложение 1.
Обработка результатов представлены в таблице 4.
Таблица 4
Показатели уровня знания младших школьников о математических понятиях
| Уровни | Количество обучающих | |
| Абсолютное число | % | |
| Высокий | ||
| Средний | ||
| Низкий | ||
| Итог |
Более наглядно представим с помощью диаграммы (рис. 1)
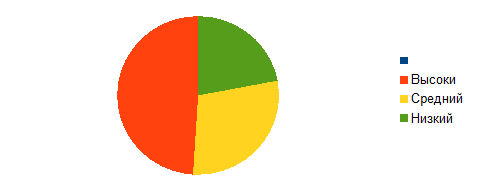
Рис. 1. Уровень знаний младших школьников о математических понятиях
На основе данных таблицы и диаграммы можно сделать вывод о том, что большинство учащихся 49% находятся на высоком уровне знания о математических понятиях. У 29% детей средний уровень, у 22% - низкий уровень.
Приведем пример результатов исследования ученика Романа Р. Обучающий выполнил данное задание на высоком уровне. Он определил все понятия правильно. Подчеркнул правильно все существенные признаки в этих определениях.
Работы учеников представлены в приложение 2, 3 и 4.
Методика 2.
Цель: выявить уровень знаний младших школьников в решение заданий связаные с понятием равенства, неравенства и множество.
Содержание: Решить задния.
1. Поставь знак <,> или =.
3577 3568 3м 4см
19991 19995 50дм 50см
65789 65789 90мм 9см
2. Назови 3 элемента множества классов в матемтике.
3. Сколько элементов содержит а) множество дней недели
б) множество букв русского алфавита
4. Где нарисовано пересечение множеств А и В, обведи в кружок.
5. Где нарисовано объедение множеств А и В, обведи в кружок.
Оборудование: лист А4, ручка.
Обработка результатов:
Максимальное количество баллов, которое может получить школьник за правильное выполнение заданий — 5 баллов.
Интерпретация полученных результатов производится следующим образом:
5 баллов — высокий уровень;
4 - 3 балла — средний уровень;
2-0 баллов — низкий уровень.
Полученные результаты методики 2 представлены в таблице 5 в приложение 5.
Обработка результатов представлены в таблице 6.
Таблица 6
Показатели уровня знаний младших школьников в решение заданий связаные с понятием равенства, неравенства и множество
| Уровни | Количество обучающих | |
| Абсолютное число | % | |
| Высокий | ||
| Средний | ||
| Низкий | ||
| Итог |
Более наглядно представим с помощью диаграммы (рис. 2)
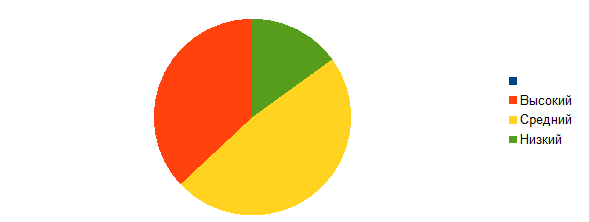
Рис. 2. Уровень знаний младших школьников в решение заданий связаные с понятием равенства, неравенства и множество
На основе данных таблицы и диаграммы можно сделать вывод о том, что большинство учащихся 37% находятся на высоком уровне знания в решении заданий. У 48% детей средний уровень, у 15% - низкий уровень.
Приведем пример результатов исследования ученицы Юлии С. Обучающаяся выполнила задания на среднем уровне. Была сделана ошибка в нахождение в том, что не правильно нашла объединение множеств А и В. Все остальные задания были сделаны хорошо, без ошибок.
Работы учеников представлены в приложениях 6, 7 и 8.
Методика 3.
Цель: выявить уровень знания младших школьников объяснять выбор постановки знака <, > или =.
Содержание: Объясни свой выбор в постановке знака <,> или =.
1. 341+562 784-123
2. 159м 159дм
Оборудование: лист А4, ручка.
Обработка результаов: Максимальное количество баллов, которое может получить школьник за выполнение этих заданий — 3 быллов.
Интерпретация полученных результатов производится следующим образом:
3 баллов — высокий уровень;
2 балла — средний уровень;
1-0 баллов — низкий уровень.
Полученные результаты методики 3 представлены в таблице 7 в приложение 9.
Обработка результатов представлены в таблице 8.
Таблица 8
Показатели уровеня младших школьников в объяснение выбора постановки знака <, > или =.
| Уровни | Количество обучающих | |
| Абсолютное число | % | |
| Высокий | ||
| Средний | ||
| Низкий | ||
| Итог |
Более наглядно представим с помощью диаграммы (рис. 3)
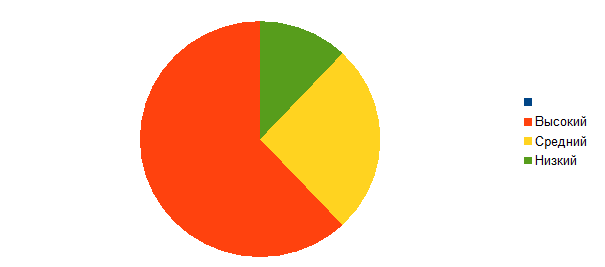
Рис. 3. Уровень знания младших школьников объяснять выбор постановки знака <, > или =
На основе данных таблицы и диаграммы можно сделать вывод о том, что большинство учащихся 62% находятся на высоком уровне знания в объяснение выбора постановки знака<, > или = . У 26% детей средний уровень, у 12% - низкий уровень.
Приведем пример результатов исследования ученика Максима М. Обучающий выполнил данное задание на низком уровне. Он не с мог правильно поставить знаки, и объяснить выбор постановки знака.
Работы учащихся представлены в приложениях 10, 11 и 12.
Итоговые результаты, полученные в ходе констатирующего эксперимента, помещены в приложение 13 в таблице 9.
На основе полученных результатов была составлена процетная характеристика уровня знаний младших школьников об математических отношенияхв 4 «а» МБОУ СОШ№27 г. Череповца, которая отображена а таблице 10.
Таблица 10
Уровни знаний младших школьников об математических отношениях в 4 «а» МБОУ СОШ№27 г. Череповца
| Уровни | Количество обучающихся | |
| Абсолютное число | % | |
| Высокий | ||
| Средний | ||
| Низкий | ||
| Итог | 100% |
Для наиболее наглядного представления отразим данные в диаграмме (рис. 4)
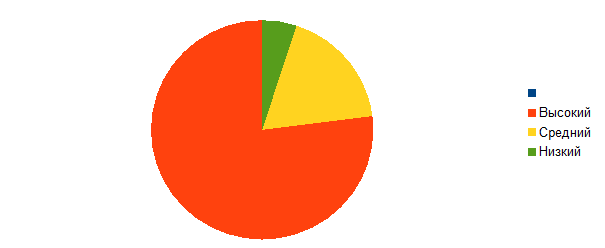 |
Рис. 4. Уровнь знания младших школьников об математических отношенияхв 4 «а» МБОУ СОШ№27 г. Череповца
Таким образом, после проведения подобранных методик было выявлено количество учеников на каждом из уровней. Большая часть обучающихся имеет высокий уровень знания младших школьников об математических отношения — 77%. На низком уровне находятся 18%. И 5% учащихся находятся на среднем уровне.
Для повышения уровня необходимо создать условия, мотивирующие младшего школьника к изучению математических отношений. Для реализации данной цели была выделена педагогическое условие, которое отражено в гипотезе исследования.
