Постановка начальной задачи.

Введение.

Разработано несколько разных методов для исследования разрешимости нелинейных дифференциальных уравнений в частных производных первого порядка. Например, всем известный классический метод характеристик, метод Галеркина, метод потоков. Как и любой метод, каждый из них имеет свои преимущества и свои недостатки. Нельзя выделить какой-либо метод, позволяющий решать любые дифференциальные уравнения в частных производных первого порядка. Каждый из известных методов хорошо применим только к определенному классу уравнений. Если, например, обратиться к тому же самому методу характеристик, то оказывается, что он с успехом применяется лишь в случае, когда коэффициенты перед производными не содержат неизвестных функций. А для систем квазилинейных дифференциальных уравнений или решения нелинейных дифференциальных уравнений реально его применять довольно сложно. В первую очередь, это связано с тем, что при применении метода характеристик для таких уравнений в соответствующем интегральном уравнении появляется суперпозиция неизвестных функций. В последнее время широкое развитие получил, в частности, метод дополнительного аргумента. Он позволяет свести решение исходной задачи к интегральному уравнению или системе интегральных уравнений. В этом уравнении неизвестная функция зависит от трех независимых переменных, но сами уравнения достаточно простые по своей структуре. Для них достаточно просто доказать существование дифференцируемого решения, исследовать качественные свойства решения, а также построить численное решение. В частности, для этого можно использовать метод последовательных приближений. Сущность метода дополнительного аргумента, его применение к решению нелинейных дифференциальных уравнений рассматриваются далее.

Заключение.

Таким образом, метод дополнительного аргумента может быть эффективно использован для приближённого решения нелинейных дифференциальных уравнений в частных производных.

В работе исходное дифференциальное уравнение преобразовано в систему из двух квазилинейных уравнений. А посредством метода дополнительного аргумента эта система сведена к системе интегральных уравнений, достаточно простых по структуре. Затем эта система решается с помощью численных методов с последующей реализацией на ПК. Получены трёхмерные графики функции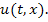

Доказательство существования решения задачи Коши (1) – (2) позволяет применять метод аргумента для решения уравнения (1) с различными функциями 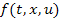, что иллюстрируется примерами.

Литература

1. Алексеенко, С. Н., Эгембердиев Ш. А. Применение метода дополнительного аргумента к одномерному аналогу задачи протекания // Материалы IV научной конференции КРСУ, Бишкек, май 1997г. – Бишкек: КРСУ, 1997.-С.26.

2. Алексеенко, С. Н., Эгембердиев Ш. А. Применение метода дополнительного аргумента к системе нелинейных уравнений типа полной производной по времени // Исслед. по интегродифференциальным уравнениям. – Бишкек: Илим, 1997. – Вып.26. - С. 161-169.

3. Алексеенко, С. Н., Эгембердиев Ш. А. Применение метода дополнительного аргумента к одномерному варианту задачи протекания с краевыми условиями третьего типа для скорости // Исслед. по интегродифференциальным уравнениям. – Бишкек: Илим, 1998. – Вып.27. - С. 225-243.

4. Алексеенко, С. Н., Эгембердиев Ш. А. Решение системы уравнений в частных производных первого порядка с начально-краевыми условиями методом дополнительного аргумента // Традиции и новации в культуре университетского образования (КТУ): Сб. трудов международ. науч. конференц. – Бишкек: Технология, 1998. – С.106-112.

5. Смирнов В. И. Курс высшей математики. Т. IV, Физматгиз. 1958.

6. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. Изд. «Наука». М. 1970. 280 с.

Оглавление

Введение. 1

Постановка начальной задачи. 2

Применение метода дополнительного аргумента к решению характеристической системы. 3

Доказательство эквивалентности систем (8) и (26). 6

Доказательство существования решения задачи Коши 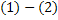.............. 12

Постановка задачи численного расчёта. 30

Дискретизация исходной задачи и её решение итерациями. 34

Программа и её описание. Результаты вычислений. 36

Заключение. 51

Литература. 52

Введение.

Разработано несколько разных методов для исследования разрешимости нелинейных дифференциальных уравнений в частных производных первого порядка. Например, всем известный классический метод характеристик, метод Галеркина, метод потоков. Как и любой метод, каждый из них имеет свои преимущества и свои недостатки. Нельзя выделить какой-либо метод, позволяющий решать любые дифференциальные уравнения в частных производных первого порядка. Каждый из известных методов хорошо применим только к определенному классу уравнений. Если, например, обратиться к тому же самому методу характеристик, то оказывается, что он с успехом применяется лишь в случае, когда коэффициенты перед производными не содержат неизвестных функций. А для систем квазилинейных дифференциальных уравнений или решения нелинейных дифференциальных уравнений реально его применять довольно сложно. В первую очередь, это связано с тем, что при применении метода характеристик для таких уравнений в соответствующем интегральном уравнении появляется суперпозиция неизвестных функций. В последнее время широкое развитие получил, в частности, метод дополнительного аргумента. Он позволяет свести решение исходной задачи к интегральному уравнению или системе интегральных уравнений. В этом уравнении неизвестная функция зависит от трех независимых переменных, но сами уравнения достаточно простые по своей структуре. Для них достаточно просто доказать существование дифференцируемого решения, исследовать качественные свойства решения, а также построить численное решение. В частности, для этого можно использовать метод последовательных приближений. Сущность метода дополнительного аргумента, его применение к решению нелинейных дифференциальных уравнений рассматриваются далее.

Постановка начальной задачи.

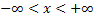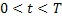В области и рассмотрим нелинейное дифференциальное уравнение:

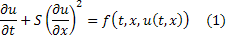
И пусть задано следующее начальное условие

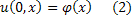
Продифференцируем данное уравнение по х:

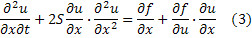
Обозначим 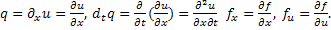Тогда уравнение (3) перепишется в виде:

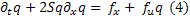
Исходное уравнение (1) в наших новых обозначениях перепишется так:

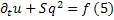
Преобразуем его так:

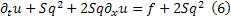
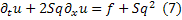
Запишем характеристическую систему для уравнения (1) относительно неизвестных функций :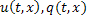

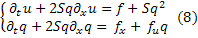
Таким образом, нелинейное уравнение (1) м свели к системе из двух квазилинейных уравнений (8). С учётом (2) зададим начальное условие для функции :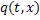

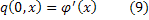
Покажем, что функция 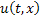, определяемая системой уравнений (8) и начальными условиями (2) и (9), будет являться искомым решением уравнения (1) с начальным условием (2). Для этого достаточно показать, что

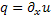
Продифференцируем первое уравнение системы по x:

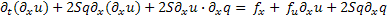(10)

Вычтем из получившегося равенства второе уравнение системы:

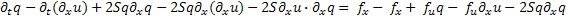(11)

Обозначим через 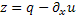, тогда из равенство (11) перепишется в виде:

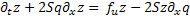или:

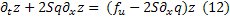
При всех 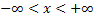и 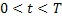функция 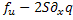ограничена. Кроме того,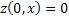

.

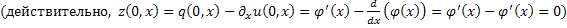Значит, можно определить константу 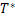, что при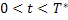 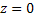. А это и означает, что
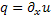, а значит функция 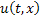, определяемая системой уравнений (8) и начальными условиями (2) и (9), будет являться искомым решением уравнения (1) с начальным условием (2), что и требовалось доказать.