Определение и основные свойства

Пусть L — простая кривая, r(t), a£t£b, — ее радиус-вектор.

Разобьем сегмент [а, b] на части точками

а=t₀<t₁,…,<t_n=b

Отметим на кривой L точки М_i, отвечающие значениям t_i, и построим ломаную M₀M₁... М_п-1М_п, вписанную в кривую L (рис. 12).

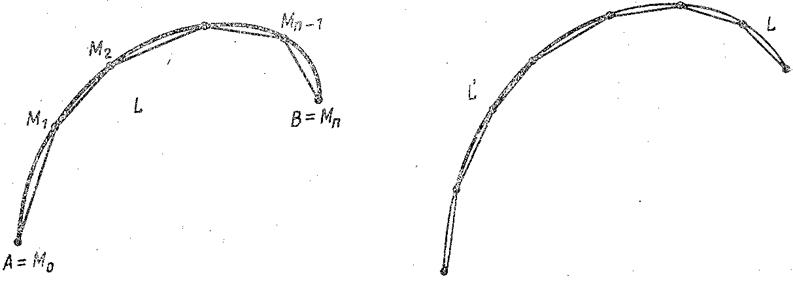
Рис. 12. Ломаная M0M1,... Мп-1Мп правильно вписана в кривую L

Рис. 13. Всякую ломаную, правильно вписанную в простую кривую V, можно достроить до ломаной, вписанной в кривую L

Определение. Кривая L называется спрямляемой, если множество длин всевозможных ломаных, вписанных в простую кривую L указанным выше способом, ограничено. Точная верхняя грань этого множества называется длиной дуги кривой L или просто длиной кривой L.

Свойства длины дуги кривой.

1. Если простая кривая L'является частью спрямляемой простой кривой L, то кривая L'также спрямляема.

Всякая ломаная, вписанная в L', является частью ломаной, вписанной в L (рис. 13). Поэтому множество длин ломаных, вписанных в кривую L', ограничено, т. е. кривая L'спрямляема.

Ясно, что длина дуги кривой L'меньше длины дуги кривой L.

2. Если простая кривая L разбита точкой N на спрямляемые части L'и L", то кривая L спрямляема и для длин s(L'), s(L") и s(L) дуг кривых L', L"и L выполняется соотношение

s(L') + s(L")=s(L).

Рассмотрим произвольную ломаную, вписанную в кривую L (рис. 14).

Добавим к ее вершинам точку N.

Получим новую ломаную, длина которой больше длины исходной ломаной и равна сумме длин ломаных, вписанных в кривые L'и L".

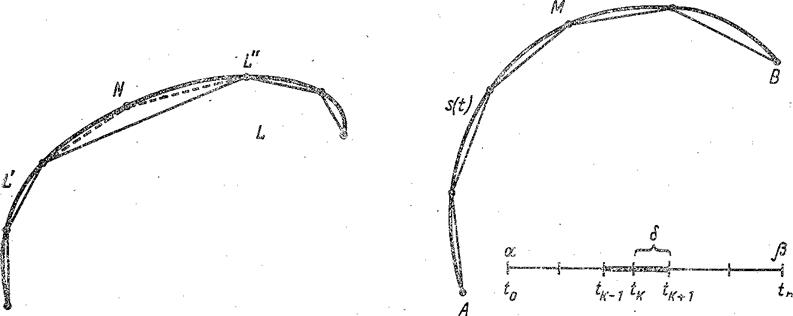
Рис. 14. Объединение ломаных, вписанных в кривые L' и L", правильно вписано в кривую L=L'ÈL"

Рис. 15. Разбиению отрезка изменения параметра соответствует вписанная в кривую ломаная

Отсюда следует, что множество длин ломаных, вписанных в кривую L, ограничено сверху числом s(L')+s(L").

Так как мы всегда можем выбрать вписанную в кривую L и содержащую вершину N ломаную так, что ее длина будет отличаться от s(L')+s(L") меньше чем на заданную положительную величину, то s(L')+s(L") — точная верхняя грань длин ломаных, вписанных в кривую L.

Тем самым s(L)=s(L')+s(L").

Пусть А и В — граничные точки спрямляемой кривой L, М — точка кривой L, соответствующая некоторому значению i из сегмента [а, b], j(t),y(t),χ(t) — координаты векторной функции r(t).

Обозначим через s(t) длину дуги кривой AM (рис. 15).

3. Функция s(t) строго монотонна и непрерывна на сегменте [а, b] и положительна при t>a.

Положительность s(t) очевидна.

Монотонность вытекает из свойства 2.

Доказательство непрерывности предварим вспомогательными рассмотрениями.

а) Пусть e — любое положительное число. Из определения длины дуги вытекает существование вписанной в кривую L ломаной, длина которой отличается от длины кривой L меньше чем на e/2. Естественно рассматривать ломаную, имеющую точку М одной из своих вершин.

Ясно, что и длина части этой ломаной, вписанной в кривую AM, отличается от ее длины s(t) меньше чем на e/2.

Конечно, длина любого звена рассматриваемой ломаной отличается от длины стягиваемой ею дуги меньше чем на e/2.

б) Длины звеньев ломаной со свойством а) можно считать меньше e/2. Действительно, из свойства равномерной непрерывности координат j(t),y(t),χ(t) радиуса-вектора r(t) кривой L на сегменте [а, b] вытекает, что по данному e>0 найдется такое положительное число d, что при разбиении сегмента [а, b] на частичные сегменты [t_i-1, t_i], t=1, 2, п, с длинами меньше d колебания функций j(t),y(t),χ(t) на каждом частичном сегменте [t_i-1, t_i],будут меньше e/(2Ö3). Тогда длина i-го звена ломаной будет меньше e/2:

в) Рассмотрим ломаную со свойствами а) и б). Дуга, стягиваемая произвольным звеном этой ломаной, имеет длину, меньшую e. В самом деле, по свойству а) длина такой дуги отличается от длины стягивающего ее звена меньше, чем на e/2, а по свойству б) длина любого звена меньше e/2.

Докажем теперь непрерывность функции s(t).

По данному e>0 построим ломаную со свойствами а), б), в) и соответствующее этой ломаной разбиение сегмента [а, b]. Пусть точка М на кривой L отвечает значению t=t_k.

Обозначим через d наименьшую из длин сегментов [t_k-1,t], [t, t_k+1].

Если 0<Dt<d, то s(t)<s(t+Dt) <s(t_k+1). Отсюда вытекает, что

0 < s(t+Dt) − s(t) < s(t_k+1) − s(t) < e,

так как длина дуги, стягиваемой звеном ломаной, меньше e.

Случай (−d)<Dt <0 рассматривается аналогично. Таким образом,

|s(t+Dt) − s(t)|<e,

если только |Dt|< d.

В силу произвольности выбора точки М на кривой L непрерывность функции s(t) на сегменте [а, b] доказана. *

Пусть S — длина кривой L. Вследствие того что функция s=s(t) на сегменте [а, b] строго возрастает от нуля до S и непрерывна, на сегменте [0, S]существует строго возрастающая и непрерывная функция t=t(s). Это означает, что параметр t на спрямляемой кривой есть строго монотонная и непрерывная функция длины дуги s. Отсюда следует, что на спрямляемой простой кривой в качестве параметра может быть выбрана длина дуги s.

Такая параметризация спрямляемой кривой называется натуральной или естественной, а параметр s (длина дуги) — натуральным параметром.

Задача. Доказать, что для спрямляемости простой кривой L необходимо и достаточно, чтобы функции j(t),y(t),χ(t) были функциями ограниченной вариации.

Замечание. Понятие длины дуги можно ввести и для кривых, заданных параметрически. Длина дуги такой кривой по определению равна сумме длин простых кривых, из которых она составлена, при условии, что эта сумма ограничена. И в этом случае длина дуги может быть параметром на кривой.