Кривая как линия пересечения поверхностей

Пусть F₁(x, у, z)=0 и F₂(x, у, z)=0 —.уравнения поверхностей Ф₁ и Ф₂ соответственно.

Систему

F₁(x, y, z)=0, F₂(x, у, z)=0

можно рассматривать как уравнения линии пересечения поверхностей Ф₁ и Ф₂ — кривой L (рис.6).

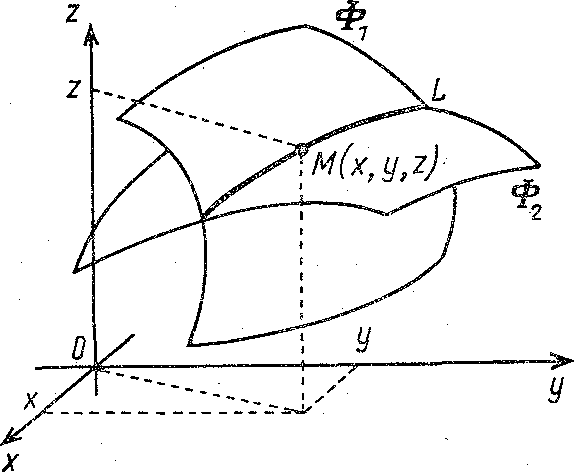
Рис. 6. Пространственная кривая как линия пересечения поверхностей

Действительно, уравнениям (6) удовлетворяют координаты х, y, z любой точки М этой кривой.

Если разрешить систему уравнений (6) относительно, например, у и z, т. е. найти у и z как функции х:

у=y(х), z=z(х),

(это возможно в некоторой окрестности точки М кривой L при условии

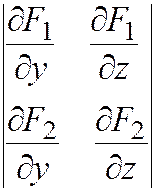¹0

в самой точке М) и затем выбрать х за параметр t, то мы получим параметрические уравнения кривой

x =t, y =y(t), z =χ(t).

Пример. Кривая Вивиани[1] представляет собой линию пересечения сферы радиуса а и круглой цилиндрической поверхности диаметра а, одна из образующих которой проходит через центр сферы.

Если поместить начало координат в центр этой сферы, а ось Oz направить по образующей цилиндрической поверхности, то уравнения сферы Ф₁ и цилиндрической поверхности Ф₂ примут вид

х²+у²+z²=а², х²+у²−ах=0.

Это и есть уравнения кривой Вивиани (рис. 7).

Если выбрать х за параметр t, то из приведенной системы получим параметрические уравнения отдельных частей (в зависимости от выбора знаков перед корнями) кривой Вивиани:

x=t, y= 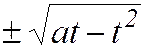, z= 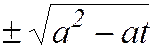, 0≤t≤a.

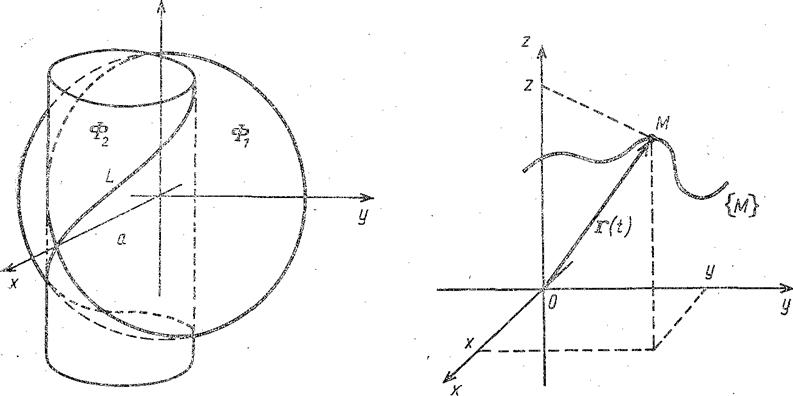
Рис. 7. Кривая Вивиани — линия пересечения сферы и цилиндра

Рис. 8. Годограф векторной функции

5. Кривая как годограф векторной функции

Пусть {t} — связное множество точек на прямой R (сегмент, полусегмент, интервал, открытая или замкнутая полупрямая, вся прямая).

Будем говорить, что на множестве {t} задана векторная функция r=r(t), если каждому значению tÎ{t} по определенному правилу ставится в соответствие вектор r(t).

Если откладывать все векторы от начала координат, то при изменении параметра t по множеству {t} конец М вектора r(t) опишет некоторое множество {М}, которое называется годографом векторной функции r(t) (рис. 8).

Для векторных функций в полной аналогии со скалярными функциями вводятся понятия предела и непрерывности. 14

Сформулируем соответствующие определения.

Вектор b называется пределом векторной функции r= r(t) при t®a (в точке а), если для любого e>0 существует d>0, такое, что для всех tÎ{t}, удовлетворяющих условию 0<|t−а|<d, выполняется неравенство |r(t)−b|<e.

Обозначения: r(t)®b, lim r(t)=b при t®a.

Векторная функция r=r(t) называется непрерывной в точке t₀Î{t}, если r(t)®r(t₀) при t®t₀.

Векторная функция называется непрерывной на множестве {t}, если она непрерывна в каждой его точке.

Пусть задана векторная функция r=r(t), tÎ{t}.

Тогда координаты х, у, z переменного вектора г(/) также будут функциями параметра tÎ{t}

х=j(t), y=y(t), z=χ(t), (7)

При этом если i, j, k — единичные векторы координатных осей, то

r(t)= j(t)i+y(t)j+χ(t)k

Отметим, что если функции (7) заданы, то их можно считать координатами векторной функции r=r(t). Легко видеть, что если r(t)®b, то функции (7) имеют пределы при t®a, равные соответствующим координатам вектора b.

Из непрерывности r(t) в точке а следует непрерывность функций (7) в точке а.

Верно и обратное: из существования пределов при t®a функций (7) вытекает существование предела при t®a векторной функции r(t) скоординатами (7).

Аналогично и для непрерывности.

УТВЕРЖДЕНИЕ. Если векторные функции r(t), R(t) и скалярная функция l(t) непрерывны, то функции r(t)±R(t), l(t)r(t), r(t)•R(t), r(t)´R(t) также непрерывны.

Докажем, например, непрерывность функции r(t)•R(t).

Пусть j(t),y(t),χ(t) — координаты векторной функции r(t) и F (t), Y(t), X(t) — координаты векторной функции R(t). Тогда

r(t)•R(t)= j(t)F (t)+y(t)Y(t)+χ(t)X(t).

Так, как из непрерывности скалярных функций следует непрерывность, их произведения и суммы, то из последнего равенства можно заключить, что скалярное произведение r(t)•R(t) непрерывно. ∎

Пубть r=r(t) — непрерывная на сегменте [a, b] векторная функция. В случае, когда различным значениям параметра t из этого сегмента отвечают различные значения векторной функции, ее годограф — простая кривая.

Можно говорить также, что кривая, заданная параметрически при помощи соотношений (7), является годографом векторной функции r=r(t) с координатами (7). Иными словами, параметрическое и векторное задания кривой, равносильны.

Мы будем использовать следующую терминологию: «кривая L задана векторной функцией r=r(t)» или «r=r(t) — вектор кривой L».

§ 2. ГЛАДКИЕ И РЕГУЛЯРНЫЕ КРИВЫЕ

Касательная к кривой

Пусть кривая L задана параметрическими уравнениями

х=j(t), y=y(t), z=χ(t), tÎ{t}

(функции j(t),y(t),χ(t) непрерывны на множестве {t}).

Обозначим через М₀ точку кривой L, отвечающую значению t₀ параметра, а через М — точку кривой L, отвечающую значению t параметра из некоторой окрестности значения t₀.

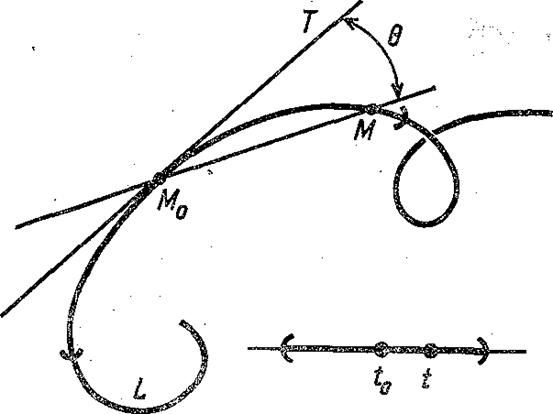
Рис. 9. Окрестность точки М₀ на кривой L — множество точек М кривой, отвечающих значениям t параметра из окрестности t₀; М₀Т — касательная к кривой L в точке М₀.

Ясно, что М®М₀, если t®t₀.

Прямая М₀Т называется касательной к кривой L в точке М₀, если при М®М₀ меньший угол q между этой прямой и переменной прямой М₀М стремится к нулю (рис. 9).

Гладкие кривые

Кривая L называется гладкой в точке М₀, если в этой точке существует касательная к кривой L и некоторая окрестность точки М₀ на кривой L однозначно проектируется на эту касательную.

Точки кривой, в которых она не является гладкой, называются особыми (рис. 10).

Кривая L называется гладкой, если она является гладкой в каждой точке и касательные в точках кривой L изменяются непрерывно. Последнее означает, что если М и N — любые точки кривой L, то при M®N касательная в точке М стремится к касательной в точке N (наименьший угол между этими касательными стремится к нулю).

Рис. 10. а) — кривая L₁ не имеет касательной в точке М₁;б) — в точке М₂ кривая L₂ имеет касательную M₂T, но никакая окрестность точки М₂ на кривой L₂ не проектируется однозначно на М₂Т (например, точки А и В проектируются в одну и ту же точку С)

Пример. Кривая

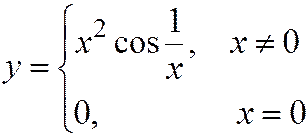
гладкая в любой своей точке, но никакая окрестность точки О(0, 0) не является гладкой кривой.