Основы теории конвективного теплообмена
 Передача теплоты конвекцией, всегда связана с теплопроводностью. Совместный процесс конвекции и теплопроводности называется конвективным теплообменом.
Передача теплоты конвекцией, всегда связана с теплопроводностью. Совместный процесс конвекции и теплопроводности называется конвективным теплообменом.
Различают конвекцию вынужденную (движение жидкости создается искусственно) и свободную — движение возникает в связи с ее нагреванием и изменением плотности.
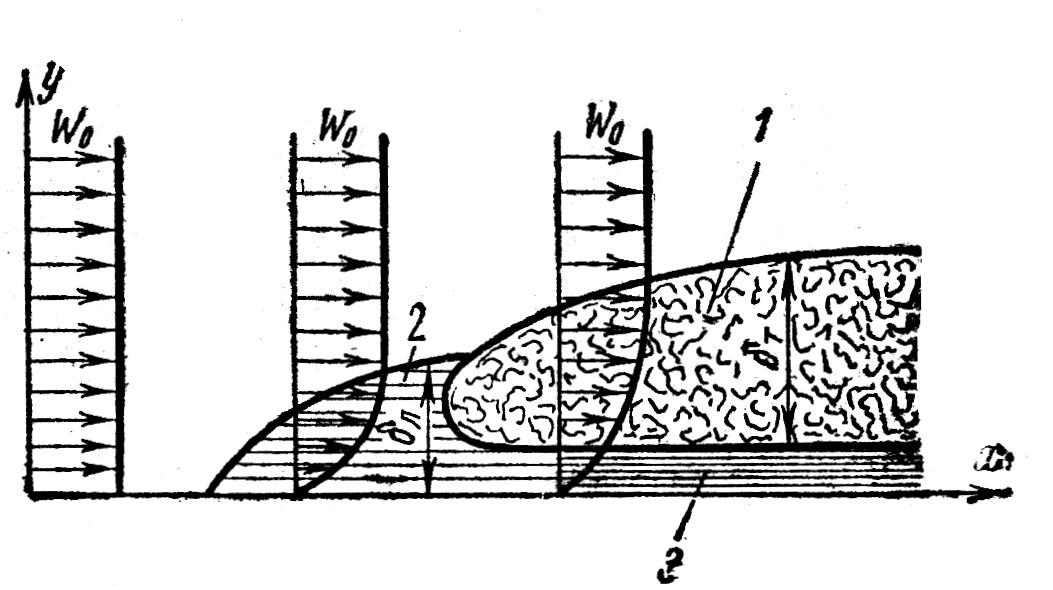
Жидкость движется спокойно, без пульсаций, образуя струи, следующие очертаниям канала. Движение такого рода называется ламинарным.
Второй вид потока называется турбулентным, в нем непрерывно происходит перемешивание всех слоев жидкости. Каждая частица потока, перемещаясь вдоль канала с некоторой скоростью, совершает различные движения перпендикулярно стенкам канала.
Коэффициент теплоотдачи. Дифференциальное уравнение теплообмена
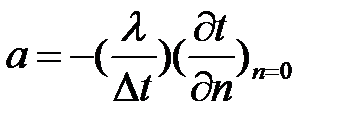
Дифференциальное уравнение описывает процесс теплообмена на поверхности канала (п= 0).
Система дифференциальных уравнений состоит из уравнений энергии (или теплопроводности), теплообмена, движения и сплошности.
Дифференциальное уравнение энергии устанавливает связь между пространственным и временным изменением температуры в любой точке движущейся жидкости:
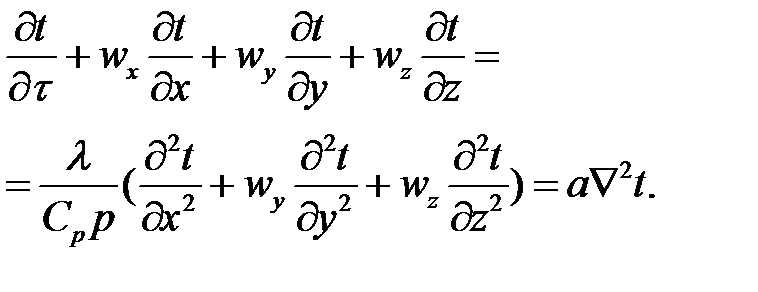
Если wx = wy = wz = 0, уравнение энергии переходит в уравнение теплопроводности для твердых тел (если отсутствуют внутренние источники теплоты).
Дифференциальное уравнение теплообмена выражает условия теплообмена на границе твердого тела и жидкости:
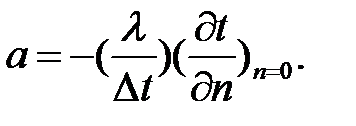
Дифференциальное уравнение движения вязкой несжимаемой жидкости представлено уравнением Навье - Стокса:
для оси х
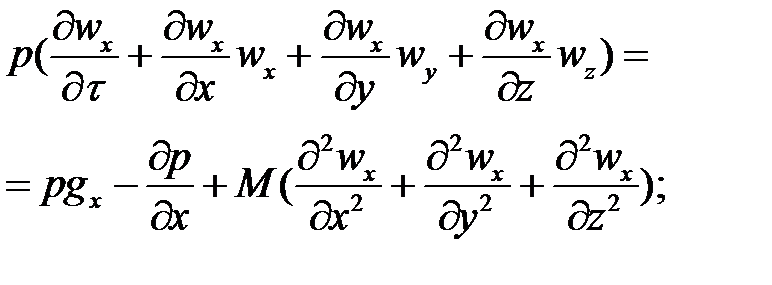
Дифференциальное уравнение сплошности, или непрерывности, для сжимаемых жидкостей имеет вид:
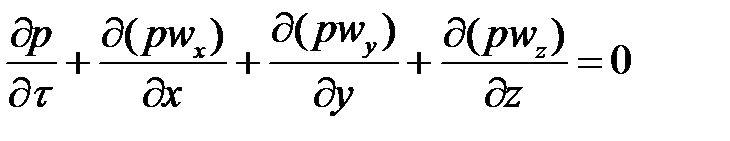 .
.
Для несжимаемых жидкостей при р = const уравнение сплошности принимает вид
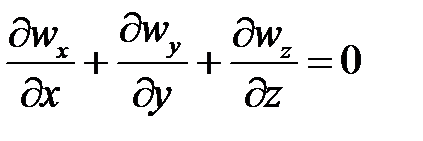 .
.
Основы теории подобия
Любое дифференциальное уравнение (или система уравнений) является математической моделью целого класса явлений. Следовательно, под классом понимается такая совокупность явлений, которая характеризуется одинаковым механизмом процессов и одинаковой физической природой.
Чтобы получить из множества решений одно частное, надо знать все характерные особенности данного явления, выделяющие его из всего класса однородных явлений. Эти дополнительные условия, которые вместе с дифференциальным уравнением однозначно определяют единичное явление, называют условиями однозначности. Условия однозначности должны содержать все особенности данного конкретного явления.
Числа подобия
Константы подобия имеют одинаковое значение для конечных и бесконечно малых величин.
Равенство можно представить в виде:
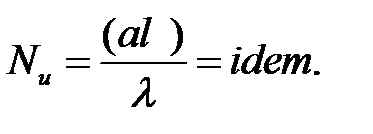
Если имеется отношение двух каких-либо однородных величин, то оно называется симплексом. Однородными называют физические величины, имеющие одинаковое физические содержание и размерность.
Теоремы подобия
Первая теорема может быть сформулирована еще и так: у подобных явлений числа подобия численно одинаковы.
Вторая теорема подобия гласит: если физическое явление описывается системой дифференциальных уравнений, то всегда существует возможность представления их в виде уравнений подобия, или интеграл дифференциального уравнения (или системы уравнений) может быть представлен как функция чисел подобия дифференциального уравнения. Вторая теорема утверждает, что операция интегрирования не из: меняет вида чисел подобия.
Третья теорема исходит из предположения, что явления протекают в геометрически подобных системах (поэтому геометрическое подобие систем есть первое необходимое условие для существования подобия), что для рассматриваемого явления можно составить дифференциальные уравнения, что установлено существование и единственность решения уравнения при заданных граничных условиях, что известны численные значения коэффициентов и физических параметров, входящих в дифференциальное уравнение.
