Математическая запись модели
Следующий этап моделирования – составление экономико-математической модели с помощью различных символов, которыми обозначают переменные задачи, коэффициенты и свободные члены.
Для обозначения переменных, как правило, используется буква х с соответствующим индексом i, например, х1, , х2, , х3, …, хn. При записи переменных с помощью индекса i, необходимо указывать какие переменные относятся к данной группе, например i = 1,2,…,5 или 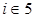 .
.
Коэффициенты при переменных величинах обозначают a или v. Они характеризуются двойной принадлежностью: соответствующему ограничению и переменной. Поэтому коэффициенты имеют два числовых индекса, первый из них характеризует принадлежность к ограничению, а второй – к переменной задачи. Так затраты ресурсов будут обозначены, например, по переменной х1 как а11, а21, а31 и т.д.
Коэффициенты при переменных в целевой функции задачи обычно обозначают с. Они имеют только один индекс, характеризующий принадлежность к той или иной переменной. Например, коэффициенты целевой функции для переменных х1, , х2, , х3 обозначают с1, с2, с3 или в общем виде сj, где 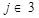 .
.
Для обозначения свободных членов уравнений или неравенств чаще всего используют букву в, В. Все свободные члены имеют также один индекс, характеризующий принадлежность этого члена к соответствующему ограничению, например, в1, , в2, , в3 или в общем виде вi 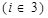 .
.
Общее количество ограничений в задаче, как правило, обозначают буквой m.
Применение одинаковых буквенных обозначений для всех коэффициентов при переменных и идентификаторов ограничений делает несложной математическую запись экономико-математической модели задачи.
Для структурной записи модели выше приведенного примера вводятся следующие обозначения:
j – индекс искомой переменной величины;
i – индекс ограничения;
xj – искомая переменная, обозначающая количество j-ой компоненты в кормосмеси;
aij – содержание i-го элемента питания в j-ом виде компоненты кормосмеси;
Cj – стоимость кормосмеси;
Bi – минимально допустимое содержание i-го питательного вещества в кормосмеси;
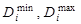 – соответственно минимальное и максимальное содержание i-го вида корма или кормовой добавки в кормосмеси;
– соответственно минимальное и максимальное содержание i-го вида корма или кормовой добавки в кормосмеси;
Qi – расчетный вес оптимизируемого количества кормосмеси;
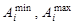 – соответственно минимально и максимально допустимое количество отдельных групп кормов в кормосмеси;
– соответственно минимально и максимально допустимое количество отдельных групп кормов в кормосмеси;
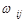 – коэффициент пропорциональности;
– коэффициент пропорциональности;
Н – множество, включающее номера переменных по видам кормов одной группы;
N – множество, включающее номера переменных по видам компонентов в кормосмеси;
M1 – множество, включающее номера ограничений во весу кормосмеси;
M2 – множество, включающее номера ограничений по содержанию питательных веществ в кормосмеси;
M3 – множество, включающее номера ограничений по содержанию отдельных групп кормов в кормосмеси;
М4 – множество, включающее номера ограничений по содержанию отдельных видов кормов.
М5 – множество, включающее номера ограничений по содержанию отдельных видов кормов в группе.
На основе введенных идентификаторов строят структурную экономико-математическую модель задачи.
Найти: 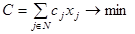
при ограничениях:
1) Суммарная масса компонентов, входящих в состав кормосмеси должна быть равна расчетной массе смеси:
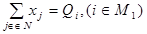
2) Кормосмесь должна содержать питательные вещества не менее допустимого количества:
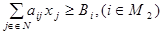
3) Удельный вес отдельных групп кормов должен находиться в зоотехнических допустимых пределах:
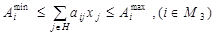
4) Отдельные виды кормов должны входить в опредеденных допустимых границах:
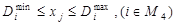
5) Удельный вес отдельных видов кормов внутри соответствующей группы должен находиться в зоотехнических допустимых нормах:
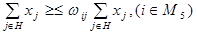
6) Ограничения по неотрицательности переменных величин: