Управляемость систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами
Рассмотрим систему, описываемую векторным дифференциальным уравнением
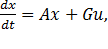
(6.1)
Где
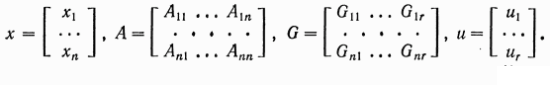 (6.2)
(6.2)
Через 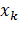 ( k=1,...,n) здесь обозначены переменные, определяющие состояние системы:
( k=1,...,n) здесь обозначены переменные, определяющие состояние системы: 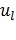 ( l=1,...,r)- приложенные к системе управляющие силы, называемые также «управлениями». Элементы матриц А и G предполагаются здесь постоянными.
( l=1,...,r)- приложенные к системе управляющие силы, называемые также «управлениями». Элементы матриц А и G предполагаются здесь постоянными.
Векторное дифференциальное уравнение (1) эквивалентно системе скалярных дифференциальных уравнений
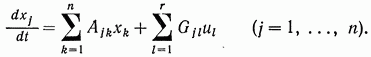 (6.3)
(6.3)
Уравнения (3) являются линейными дифференциальными уравнениями с постоянными коэффициентами, и их можно интерпретировать, например, как уравнения в вариациях относительно установившегося движения (или относительно состояния равновесия) некоторой системы материальных точек. Пусть s- число степеней свободы этой системы, а 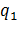 ,…,
,…, 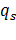 — ее обобщенные координаты. Ранг системы уравнений (3) при этом будет
— ее обобщенные координаты. Ранг системы уравнений (3) при этом будет
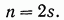
Переменные 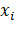 ( i=1,…,n) в уравнениях (3) могут быть фазовыми координатами или каноническими переменными (обобщёнными координатами и обобщёнными импульсами) рассматриваемой системы материальных точек или быть связанными с ними при помощи некоторого линейного преобразования.
( i=1,…,n) в уравнениях (3) могут быть фазовыми координатами или каноническими переменными (обобщёнными координатами и обобщёнными импульсами) рассматриваемой системы материальных точек или быть связанными с ними при помощи некоторого линейного преобразования.
Так как у системы материальных точек число приложенных обобщённых сил не может превышать числа степеней свободы, то число г управляющих сил :
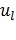 ( l=1,...,r) в дифференциальных уравнениях (3) должно удовлетворять условию
( l=1,...,r) в дифференциальных уравнениях (3) должно удовлетворять условию
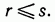
Заметим еще, что те из уравнений системы (3), которые выражают лишь зависимость между переменными 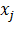 например уравнения вида
например уравнения вида
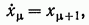 (6.4)
(6.4)
в случае, когда 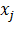 — фазовые координаты системы, требуют выполнения тождеств
— фазовые координаты системы, требуют выполнения тождеств
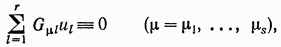 (6.5)
(6.5)
для чего необходимо, чтобы соответствующие строки матрицы G состояли из нулевых элементов
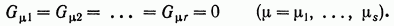 (6.6)
(6.6)
Обычно управляемая система имеет, однако, более сложную структуру. В ее состав входят еще устройства для формирования управляющих сигналов и др. При этом в число уравнений (3) могут входить также дифференциальные уравнения, описывающие программы включенных в состав системы вычислительных управляющих устройств и т. п. Эти уравнения могут содержать и свои управляющие воздействия. В этом случае будет иметь место соотношение n>2s, где под s здесь подразумевается число степеней свободы лишь совокупности механических звеньев, входящих в систему (3), а также может оказаться, что r > s.
Рассмотрим сейчас вопрос о том, можно ли систему, описываемую уравнением (1), перевести из любого заданного начального состояния в любое желаемое состояние за конечный промежуток времени, выбирая надлежащим образом закон изменения управляющих сил 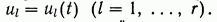 .
.
Сформулированное здесь свойство получило название управляемости. Системы, обладающие этим свойством, называются вполне управляемыми.
Так как управляемость системы определяется строением матриц А и G, то понятие управляемости относят также к этим матрицам, говоря, что пара ( A, G) вполне управляема, или соответственно неуправляема.
Перейдем к решению поставленной задачи. Закон движения системы, описываемой уравнением (1), будет следующим:
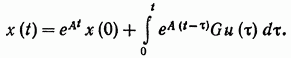 (6.7)
(6.7)
Предположим, что существует такой закон изменения управляющих сил 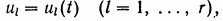 который обеспечивает приведение системы к моменту времени
который обеспечивает приведение системы к моменту времени 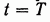 в начало координат, то есть обеспечивает выполнение условия
в начало координат, то есть обеспечивает выполнение условия
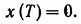 (6.8)
(6.8)
Так как согласно (7)
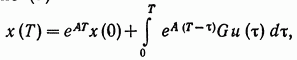 (6.9)
(6.9)
то в соответствии с (8) будем иметь следующее соотношение:
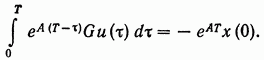 (6.10)
(6.10)
Условие управляемости системы (1) состоит в том, что ранг матрицы
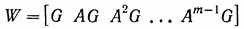
должен быть равен n.
Одним из возможных управлений является, например, управление
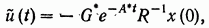
где
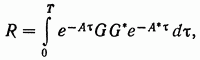
а символом * обозначена транспонированная матрица.
