Метод динамического программирования Р. Беллмана. Принцип оптимальности

Рассмотрим управляемую систему описываемую следующей системой скалярных дифференциальных уравнений:

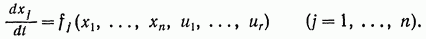(7.4)

Здесь 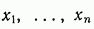— фазовые координаты системы, — управляющие силы.

Вводя векторы

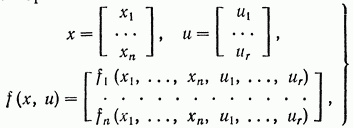(7.5)

можно заменить систему скалярных дифференциальных уравнений (4) следующим векторным дифференциальным уравнением:

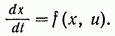(7.6)

Полагая, что на управляющие силы наложены некоторые ограничения, потребуем при выборе этих сил выполнения условия

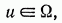(7.7)

где 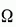— некоторая область в пространстве , определяемая видом наложенных ограничений.

Пусть целью управления является минимизация функционала

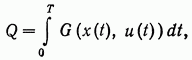(7.8)

где G — некоторая ограниченная скалярная функция переменных 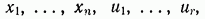, а Т — заданная фиксированная величина.

Метод динамического программирования основывается на сформулированном Р. Беллманом [8] принципе оптимальности. Этот принцип имеет место для систем, последующее движение которых полностью определяется состоянием этих систем в любой текущий момент времени. К таким системам относятся, например, системы, описываемые дифференциальными уравнениями (4), где под состоянием подразумевается положение системы в фазовом пространстве, системы, описываемые уравнениями в конечных разностях с дискретным аргументом и др. Принцип оптимальности сформулирован Беллманом так:

Оптимальное поведение обладает тем свойством, что, каковы бы ни были первоначальное состояние и решение в начальный момент, последующие решения должны составлять оптимальное поведение относительно состояния, получающегося в результате первого решения.

Указанная формулировка принципа оптимальности (названного Беллманом интуитивным) относится к системам весьма общего вида. Для управляемых систем, описываемых дифференциальными уравнениями (4), под «поведением» системы следует понимать движение этих систем, а термин «решение» относится к выбору закона изменения во времени управляющих сил.

Для систем, описываемых дифференциальными уравнениями (4), принцип оптимальности совпадает с хорошо известным фактом, что часть экстремали является снова экстремалью.

В качестве примера [85] на рис. 12 показана проходящая через заданную точку 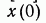оптимальная траектория системы (4), то есть траектория, минимизирующая при условии (7) функционал (8), в котором значение Т предполагается фиксированным. Значение 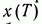предполагается здесь заранее неизвестным. Точка 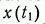разбивает рассматриваемую траекторию на два участка 1 и 2. Участку 2 соответствует функционал

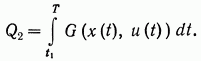(7.9)

Участок 2 может рассматриваться и как самостоятельная траектория. Эта траектория будет оптимальной, если она доставляет минимум функционалу (9).

Принцип оптимальности утверждает, что участок 2 оптимальной траектории 1—2 сам по себе является оптимальной траекторией системы (4), состояние которой при 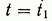есть .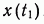

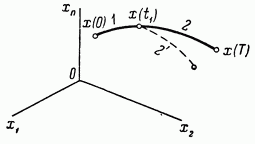
Рис. 12.

Если допустить противное, то существует (рис. 12) другая траектория 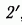доставляющая функционалу (9) значение меньшее, чем доставляет траектория 2. Но тогда на интервале времени 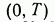оптимальной будет не траектория 1—2, а траектория 1— 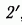. Мы пришли к противоречию с исходными данными о том, что траектория 1—2 является оптимальной. Полученное противоречие и доказывает, что участок 2 оптимальной траектории 1—2 является в свою очередь оптимальной траекторией системы (4) на интервале времени .

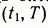Заметим теперь, что утверждения принципа оптимальности относятся к последующему за данным состоянием движению системы. Для предшествующего данному состоянию движения системы они, вообще говоря, могут не иметь места.

Так, например, если задано лишь начальное состояние системы 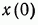, то участок 1 оптимальной траектории 1—2 может сам по себе и не быть оптимальной траекторией, то есть может и не доставлять минимума функционалу

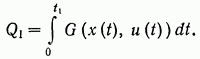(7.10)

Только в том случае, когда задана конечная точка участка 1, этот участок сам по себе также будет оптимальной траекторией.

Таким образом, для управляемых систем принцип оптимальности утверждает, что выбор оптимального управления определяется лишь состоянием системы в текущий момент времени.

Это утверждение дает возможность получения приведенных ниже функциональных уравнений, определяющих закон изменения управляющих сил в задаче об оптимальном управлении.