Задание 3: системы счисления

Перед выполнением заданий необходимо ответить на следующие вопросы:

1) Перевод целых чисел из десятичной системы счисления в любую другую позиционную систему счисления.

2) Перевод правильной десятичной дроби в любую другую позиционную систему счисления.

3) Перевод чисел из 16, 8, 2 в десятичную систему счисления

Пример выполнения задания

Перевод чисел из произвольной системы в десятичную.

Для перевода числа из любой позиционной системы счисления в десятичную необходимо использовать развернутую форму числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами. Например:

1101₂=1*2³+1*2²+0*2¹+1*2⁰=13₁₀

17D.ECH=12·16^-2 + 14·16^-1 +13·16⁰ + 7·16¹ + 1·16²=381.921875

Вариант 0. В какой системе счисления справедливо следующее:

а) 20 + 25 = 100;

б) 22 + 44 = 110?

Вариант 1. Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы:

а) 10110112;	е) 5178;	л) 1F16;
б) 101101112;	ж) 10108;	м) ABC16;

Вариант 2. Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы:

в) 0111000012;	з) 12348;	н) 101016;
г) 0,10001102;	и) 0,348;	о) 0,А416;

Вариант 3. Переведите числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:

а) 125₁₀; б) 229₁₀; в) 88₁₀; г) 37,25₁₀; д) 206,125₁₀.

Вариант 4. Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:

а) 1001111110111,01112;	г) 1011110011100,112;
б) 1110101011,10111012;	д) 10111,11111011112;

Вариант 5. Переведите в двоичную и восьмеричную системы шестнадцатеричные числа:

а) 2СE₁₆; б) 9F40₁₆; в) ABCDE₁₆; г) 1010,101₁₆; д) 1ABC,9D₁₆.

Вариант 6. Выпишите целые числа: а) от 101101₂ до 110000₂ в двоичной системе.

Вариант 7. Выпишите целые числа: б) от 202₃ до 1000₃ в троичной системе.

Вариант 8. Выпишите целые числа: в) от 14₈ до 20₈ в восьмеричной системе.

Вариант 9. Выпишите целые числа: г) от 28₁₆ до 30₁₆ в шестнадцатеричной системе.

Задание 4: алгоритмизация, постойте блок-схему для задачи

Пример выполнения задания.

Задача. Вычислите длины гипотенузы по катетам.

Постановка задачи: даны два вещественных числа, являющихся величинами катетов некоторого прямоугольного треугольника. Вычислить длину гипотенузы этого треугольника.

Решение.

Анализ задачи.

1. Входные данные. Входными данными являются длины катетов x и y.

2. Результат. Результатом работы алгоритма является вычисленное значение гипотенузы z.

3. Формулы. Гипотенуза вычисляется по формуле Пифагора

.

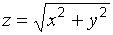Проектирование алгоритма.

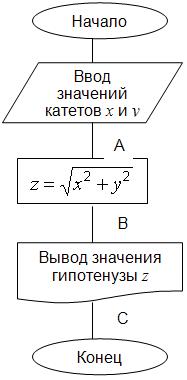
Исполнение:

Расставьте на алгоритме контрольные точки A, B, C . Контрольные точки ставятся везде, где вводятся или изменяются данные, т. е. после каждого ввода и каждого действия алгоритма (на блок-схеме контрольные точки ставятся после всех параллелограммов и прямоугольников, кроме вывода данных).

Исполнитель начинает выполнять алгоритм с его начала. При движении по алгоритму его активная точка проходит сначала контрольную точку A, затем B и наконец C.

Задаются входные данные. Пусть катет x = 3, а катет y = 4. Тогда по формуле Пифагора гипотенуза такого прямоугольного треугольника должна быть z = 5.

Задания для выполнения.

Вариант 0. Определить, является ли заданная последовательность чисел a₁ , a₂ , ... , a_N монотонно убывающей.

Вариант 1. Решить квадратное уравнение ax²+ bx + c = 0.

Вариант 2. Вычислите длину окружности, площадь круга и объём шара одного и того же заданного радиуса.

Вариант 3. Вычислите периметр и площадь прямоугольного треугольника по длинам двух его катетов.

Вариант 4. По координатам трёх вершин некоторого треугольника найдите его площадь и периметр.

Вариант 5. Определите, является ли заданное целое число А нечётным двузначным числом.

Вариант 6. Вычислить сумму элементов числового массива A = (a1 , a2 , ... , aN ).

Вариант 7. Найти наибольший элемент числового массива A = (a1, a2 , ..., aN ) и его номер.

Вариант 8. Для заданного x вычислить

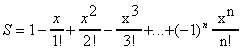
Здесь n! = 1. 2. 3 .... n (читается как "n-факториал").

Вариант 9. Элементы заданного числового массива a1, a2, ..., aN упорядочить по возрастанию.